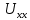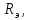001501-27 ЭП. Номер ветви Начало конец
 Скачать 267.76 Kb. Скачать 267.76 Kb.
|
|
Шифр: 001501-27 Задание согласно варианту представлено в таблице:
Составить баланс мощностей. МЭГ напряжения найти ток сопротивления R2. Найти напряжение между узлами 2 и 4 (U24). Решение Изобразим граф схемы. При этом расположим узлы таким образом, чтобы ветви не пересекались (рис. 1) 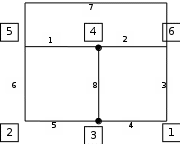   Рис. 1. Граф схемы Включим в ветви цепи сопротивления и источники ЭДС. Источники тока подключаем параллельно соответствующим ветвям (рис.2). Расчёт токов методом преобразования На схеме (рис.2) преобразуем источник тока J03 в источник напряжения E03: 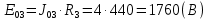 , ,а источник тока J07 в источник напряжения E07: 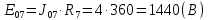 . .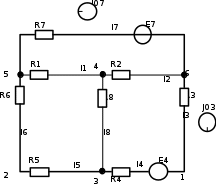 Рис. 2. Схема цепи. Полученная схема показана на рисунке 3. На этой схеме источники напряжения E7 и E07 объединены в источник напряжения 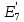 , а источники напряжения E4 и E03 объединены в источник напряжения , а источники напряжения E4 и E03 объединены в источник напряжения 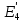 : :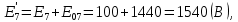 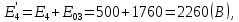 а последовательно включённые сопротивления 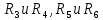 : :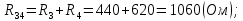 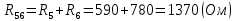 . .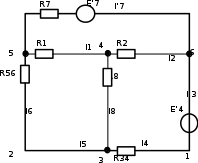 Рис. 3. Преобразованная схема цепи. Пассивный треугольник 4-5-3 преобразуем в пассивную звезду (рис.4), где 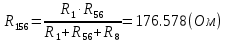 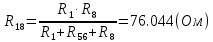 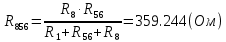 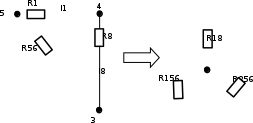 Рис.4. Преобразование «треугольник-звезда». В результате этих преобразований схема будет иметь следующий вид, представленный на рисунке 5. 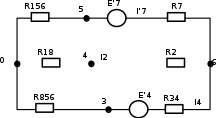 Рис. 5. Преобразованная схема цепи С целью дальнейшего упрощения схемы объединим последовательные сопротивления: 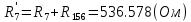 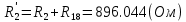 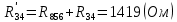 Теперь схема имеет следующий вид (рис.6): 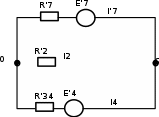 Рис. 6. Преобразованная схема цепи Далее целесообразно использовать метод узловых напряжений. Для определения напряжения 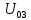 необходимо составить одно уравнение: необходимо составить одно уравнение: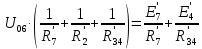 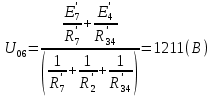 Определим токи на рисунке 6 на основании второго закона Кирхгофа: 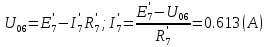 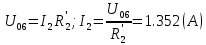 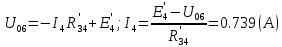 По схеме (рис. 5) определим напряжение между узлами 5 и 4: 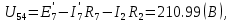 Определим ток 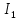 (рис. 3): (рис. 3):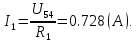 Для определения неизвестных токов 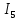 , , 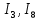 , , 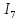 составим уравнение по первому закону Кирхгофа для узлов 5 (рис. 3), 1, 4, 5 (рис. 2): составим уравнение по первому закону Кирхгофа для узлов 5 (рис. 3), 1, 4, 5 (рис. 2):для узла 5 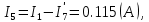 для узла 1 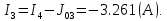 для узла 4 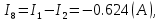 для узла 5 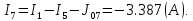 Составление баланса мощностей. ЭДС положительна при совпадающих направлениях ЭДС и тока ветви и отрицательна при противоположном направлении ЭДС и тока ветви. Мощность источника тока определяется произведением тока данного источника и напряжения на его зажимах. Она положительна при противоположных направлениях на зажимах источника тока и тока источника. Мощность, выделяемая в активных сопротивлениях, всегда положительна и равна: 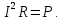 Баланс мощности записывается в виде 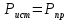 : :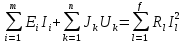 , ,где m - число источников ЭДС в схеме; n - число источников тока в схеме; f - число активных сопротивлений в схеме. Составим баланс мощностей для схемы рис. 2: 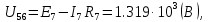 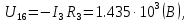 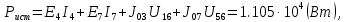 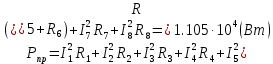 Так как мощность источников равна мощности тепловых потерь, то значения рассчитанных токов верны. Определение напряжения 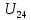 . .Для определения напряжения 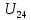 воспользуемся рисунком 2. Тогда на основании второго закона Кирхгофа можно записать: воспользуемся рисунком 2. Тогда на основании второго закона Кирхгофа можно записать: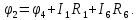 Отсюда 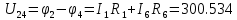 (В). (В).Определение тока в резисторе 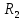 методом эквивалентного генератора методом эквивалентного генератора Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Р 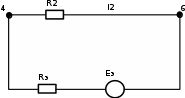 азделим электрическую цепь на две части: эквивалентный генератор и потребитель (рис. 7). азделим электрическую цепь на две части: эквивалентный генератор и потребитель (рис. 7).Рис. 7. Эквивалентная схема замещения На схеме (рис.7) искомый ток 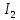 определим по закону Ома для замкнутой цепи: определим по закону Ома для замкнутой цепи: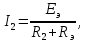 где 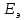 - ЭДС эквивалентного генератора, величину которой определяют как напряжение на зажимах генератора в режиме холостого хода ( - ЭДС эквивалентного генератора, величину которой определяют как напряжение на зажимах генератора в режиме холостого хода (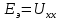 ); );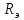 - внутреннее сопротивление эквивалентного генератора, величину которого определяют как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов. - внутреннее сопротивление эквивалентного генератора, величину которого определяют как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.Для определения напряжения на зажимах генератора в режиме холостого хода исключим из рассматриваемой цепи (рис. 2) ветвь, содержащую сопротивление R2, и представим остальную часть цепи (режим холостого хода): 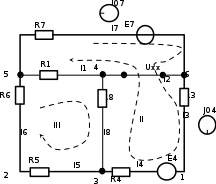 Рис. 8. Схема для расчета 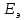 Методом контурных токов определим токи в ветвях схемы. Составим уравнения по второму закону Кирхгофа относительно контурных токов (рис.8): 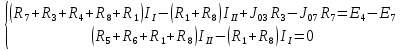 Отсюда: 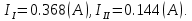 Тогда токи в ветвях схемы равны: 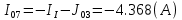 ; ;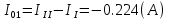 ; ;Знание токов 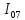 и и 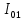 позволяет определить напряжение холостого хода: позволяет определить напряжение холостого хода: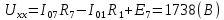 . .Для расчёта внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник (рис. 8) в пассивный, при этом источники ЭДС закорачиваются, а источники тока размыкаются: 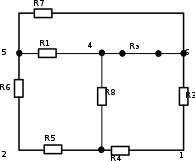 Рис.9. Схема для расчета 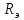 Необходимо найти сопротивление между точками 4 и 6. Заменим треугольник резисторов 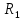 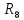 , и , и 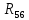 звездой. Схема замещения представлена на рисунке 10. звездой. Схема замещения представлена на рисунке 10.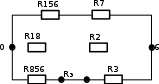 Рис. 10. Схема замещения треугольника звездой Сопротивления 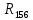 , , 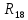 , , 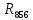 равны: равны: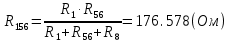 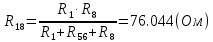 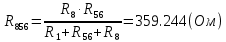 Тогда 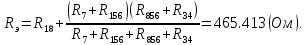 Зная 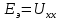 и и 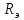 , найдем ток исследуемой ветви: , найдем ток исследуемой ветви: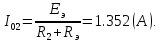 Построение потенциальной диаграммы. Для построения потенциальной диаграммы необходимо знать напряжение на всех элементах контура, а также сопротивления всех элементов контура. На рис. 11 показан контур, для которого мы будем строить потенциальную диаграмму. 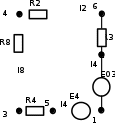 Рис. 11. Контур для построения потенциальной диаграммы Базисную точку выберем произвольно, например точку 4. Построение будем производить, обходя контур по часовой стрелке. Определим потенциалы точек: 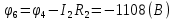 ; ;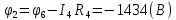 ; ;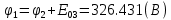 ; ;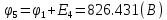 ; ;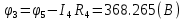 ; ;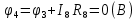 ; ;По оси абсцисс будем откладывать значения сопротивлений элементов, а по оси ординат – значения потенциалов точек. Базисную точку помещаем в начало координат (рис.12).  Результаты расчетов представим в виде таблицы:
Литература Ю.Г.Толстов, А.А. Теврюков: Теория электрических цепей. Москва: 1970; Башарин С.А., Федоров В. А.: Теоретические основы электротехники. Теория электрических цепей и электромагнитного поля. Москва: 2004г. Методическая разработка БГУИР. Интернет  |

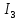 , А
, А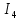
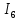 , А
, А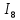 , А
, А