Поурочные разработки. алгебра 7 класс. Номера уроков Наименование разделов и тем
 Скачать 78.29 Kb. Скачать 78.29 Kb.
|
1 2 Урок 79. ТЕМА: Применение различных способов для разложения многочлена на множители Урок 80. ТЕМА: Применение преобразований целых выражений Урок 81. ТЕМА: Применение преобразований целых выражений Урок 82. ТЕМА: Контрольная работа № 8 Глава VI. Системы линейных уравнений Урок 83. ТЕМА: Линейное уравнение с двумя переменными Урок 84. ТЕМА: График линейного уравнения с двумя переменными Урок 85. ТЕМА: График линейного уравнения с двумя переменными Урок 86. ТЕМА: Системы линейных уравнений с двумя переменными Урок 87. ТЕМА: Способ подстановки Урок 88. ТЕМА: Способ подстановки Урок 89. ТЕМА: Способ сложения Урок 90. ТЕМА: Способ сложения Урок 91. ТЕМА: Решение задач с помощью систем уравнений Урок 92. ТЕМА: Решение задач с помощью систем уравнений Урок 93. ТЕМА: Решение задач с помощью систем уравнений Урок 94. ТЕМА: Контрольная работа № 9 Обобщающее итоговое повторение Урок 95. ТЕМА: Линейное уравнение с одной переменной Урок 96. ТЕМА: Системы линейных уравнений с двумя переменными Урок 97. ТЕМА: Линейная функция и ее график Урок 98. ТЕМА: Степень с натуральным показателем, одночлены Урок 99. ТЕМА: Многочлены и действия над ними Урок 100. ТЕМА: Формулы сокращенного умножения, разложение многочлена на множители Урок 101. ТЕМА: Итоговая контрольная работа № 10 Урок 102. ТЕМА: Анализ итоговой контрольной работы Выражения с переменными - урок 2 - I четверть ЦЕЛЬ УРОКА: Формирование у учащихся навыков самостоятельного применения полученных знаний (нахождение значения выражения с переменной; составление выражения с переменной по условию задачи). ПЛАН УРОКА:
ХОД УРОКА I. Организационный момент. II. Проверка домашнего задания. № 24 — с записью на доске; № 30 — устно. III. Актуализация опорных знаний (путем сочетания индивиду- альной работы по карточкам с фронтальной работой). Двое учащихся у доски выполняют задания. Первый: 1) Составить выражение для вычисления площади детали, изображенной на рисунке: 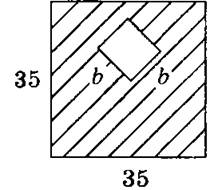 Какие значения может принимать переменная b. Какие значения b недопустимы? 2) Придумать задачу, решением которой было бы выражение 3n + 4m. Второй: 1) Составить выражение для вычисления периметра фигуры, изображенной на рисунке 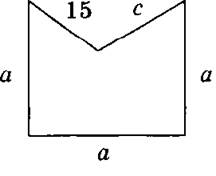 2) Придумать задачу, решением которой было бы выражение (у + 8)/t. Какие значения t недопустимы? В это время класс работает фронтально: №№ 37, 36 — устно; № 38 — письменно с последующей проверкой на доске. Затем коллективно обсуждается выполнение заданий по карточкам. IV. Тренировочные упражнения. № 22 — коллективно с записью на доске; № 25 — самостоятельно с последующей проверкой; № 26 — коллективно с записью на доске. V. Упражнения творческого характера. №№ 32, 42 — самостоятельно с последующим обсуждением ответов. VI. Самостоятельная работа (с последующей проверкой). Вариант . 1. Найти значение выражения: 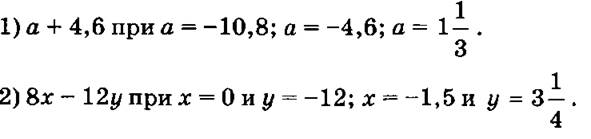 2. № 31 (рис. 1 с. 8 для первой фигуры). Вариант II 1. Найти значение выражения: 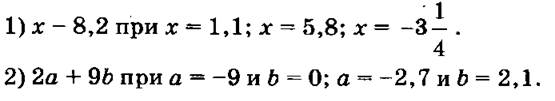 2. № 31 (рис. 1 с. 8 для второй фигуры). VII. Упражнения на повторение. №№ 44 (а), 45 — коллективно с записью на доске. VIII. Итог урока. IX. Домашнее задание. п. 2 №№ 28, 43, 46. Главная трудность первых уроков алгебры — абстрактность материала. Поэтому важно все операции, производимые с буквами, предварительно произвести с числами. При составлении выражения с переменными и формул по условию задачи желательно показать, что для решения подобных однотипных задач можно указать общий способ решения и записать его с помощью букв, т.е. обобщить. Употребление букв вместо чисел можно объяснить так: когда речь идет об определенном конкретном числе, то его записывают посредством цифр; когда же хотят сказать одновременно о разных числах, то вместо цифр пишут букву: подобно тому, как говорят: «несколько человек», «какой-то человек», «город N». На первых этапах изучения алгебры под буквой подразумевается число; в дальнейшем же переходят к собственно алгебре — операциям с буквами. Перед тем, как ввести буквенные обозначения, полезно решать арифметические задачи с целью повторения зависимостей между величинами, которые могут встретиться при составлении выражения числового (с переменными). Упражнения на чтение и запись выражений с переменными вызывают затруднения. Так, иногда учащиеся считают, что 6 + 9 не сумма, а запись действия, сумма же равна 15. То же и по отношению к разности, произведению, частному. Следует обращать их внимание, на то, что а + b — не только запись действия, но и результат его. При чтении выражений с переменными надо повторить порядок действий и сказать, что он сохраняется и в алгебре. Прежде, чем перейти к чтению выражений с переменными, целесообразно дать ученикам упражнения, в которых они определяют порядок действий. Чтение выражений начинается с последнего действия. Пример. Прочитать выражение Решение. Рассмотрим порядок действий: 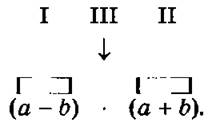 Последнее действие — умножение. Значит, данное выражение надо прочитать так: произведение разности чисел а и b на их сумму. 1 2 |
