Теория Вероятностей - варинт 4. Документ Microsoft Word. Нормальное распределение
 Скачать 72.92 Kb. Скачать 72.92 Kb.
|
|
Задача 1. Тема: «Нормальное распределение». Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 у.е., и стандартным отклонением, равным 6. Определите вероятность того, что в случайно выбранный день обсуждаемого периода цена была выше 40 за акцию. Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна: где Ф(𝑥) – функция Лапласа, 𝑚 − математическое ожидание; 𝜎 − среднее квадратическое отклонение. 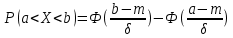 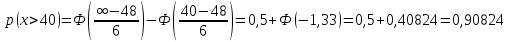 Ответ: вероятность того, что цена была выше 40 за акцию = 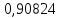 Задача 2. Тема: «Интервальные оценки». В 2014 г. выборочное обследование распределения населения города по среднедушевому доходу показало, что 40% обследованных в выборке имеют среднедушевой доход не более 20 тыс. руб. В каких пределах находится доля населения, имеющего такой среднедушевой доход, во всей генеральной совокупности, если объем генеральной совокупности составляет 1000000 единиц, выборка не превышает 10% объема генеральной совокупности и осу- 8 ществляется по методу случайного бесповторного отбора, а доверительная вероятность равна 0.9? Решение: 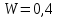 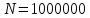 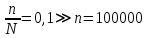 Найдем доверительный интервал для доли населения, имеющего среднедушевой доход, во всей генеральной совокупности из неравенства: 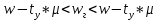 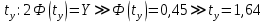 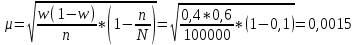 Доверительный интервал для доли: 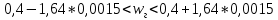 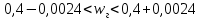 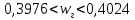 Ответ: 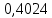 Задача 3. Тема: «Проверка статистических гипотез» Компания утверждает, что новый вид зубной пасты для детей лучше предохраняет зубы от кариеса, чем зубные пасты, производимые другими фирмами. Для проверки была отобрана случайным образом группа из 400 детей, которые пользовались новым видом зубной пасты. Другая группа из 300 детей, также случайно выбранных, в это же время пользовалась другими видами зубной пасты. Было выявлено, что у 30 детей, использующих новую 12 пасту, и 25 детей из контрольной группы появились новые признаки кариеса. Имеются ли у компании достаточные основания для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты? Уровень значимости α = 0.05. Решение: Доля детей, использующих новую пасту, у которых появились новые признаки кариеса: 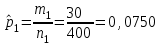 Доля детей, использующих другие виды пасты, у которых появились новые признаки кариеса: 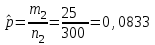 Нулевая гипотеза заключается в том, что вероятность появление новых признаков кариеса у детей в разных группах одинакова: 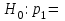 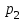 Альтернативная гипотеза заключается в том, что вероятность появление новых признаков кариеса у детей, пользующихся новой пастой ниже. чем у детей, пользующихся другими видами пасты: 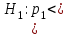 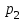 Находим численное значение критерия: 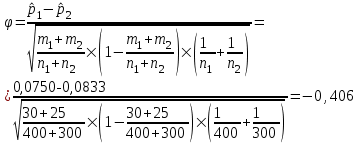 Поскольку альтернативная гипотеза 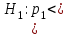 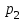 , то критическая область будет левосторонней. , то критическая область будет левосторонней.При α = 0,05 доверительная вероятность 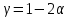 = 1 – 2×0,05 = 0,9. По таблице значений функции Лапласа находим критическую точку: = 1 – 2×0,05 = 0,9. По таблице значений функции Лапласа находим критическую точку: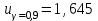 Критическая область: 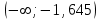 . .Вывод. Т.к. эмпирическое значение критерия 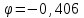 не попадает в критическую область не попадает в критическую область 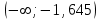 , то гипотеза об отсутствии разницы в эффектах от новой и других видов паст , то гипотеза об отсутствии разницы в эффектах от новой и других видов паст 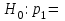 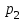 не отвергается. У компании недостаточно оснований для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты. не отвергается. У компании недостаточно оснований для утверждения о том, что новый сорт зубной пасты эффективнее предотвращает кариес, чем другие виды зубной пасты.Задача 4. Тема: «Критерий согласия Пирсона».  Для каждого из интервалов определим середину: Имеем:
Вычислим среднюю дисперсию: Определим выборочную среднюю 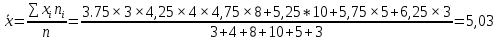 Вычислим дисперсию: 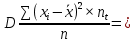 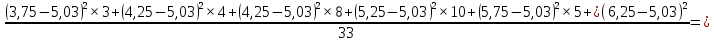 0,47 0,47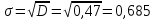 Нулевую гипотезу сформулируем как утверждение, что случайная величина имеет  распределение с указанными выше параметрами: распределение с указанными выше параметрами: 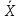 , , 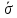 Согласно критерию Пирсона, необходимо сравнить теоретические и эмпирические частоты. Определим теоретические частоты. Если случайная величина 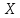 имеет нормальное распределение, то нормированная случайная величина: имеет нормальное распределение, то нормированная случайная величина: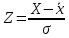 Имеет стандартное нормальное распределение, и для расчёта вероятностей можно использовать табличную форму Лапласа: 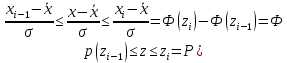 Интервал Частота Соединении интервала
Задача 5. Тема: «Ранговая корреляция». По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05.  Задача 6. Тема: «Линейная корреляция и регрессия» Некоторая фирма проводит рекламную кампанию в магазинах с демонстрацией антисептических качеств своего нового моющего средства. Через некоторое время после начала рекламной кампании фирма решила проанализировать эффективность этого вида рекламы, сопоставив еженедельные объемы продаж (X, тыс. руб.) с расходами на рекламу (Y, тыс. руб.).  |

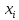 – середина интервала
– середина интервала