РГЗ тоэ. Новосибирский государственный технический университет
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
В табл. 1: I/U 1I/U 10 – значения токов в ветвях без источников тока или напряжений на источниках тока; 3. Задачи для самостоятельного решения. З 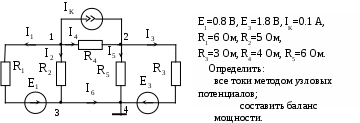 адача 1.1 адача 1.1З 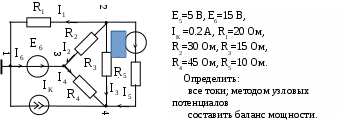 адача 1.2 адача 1.2З 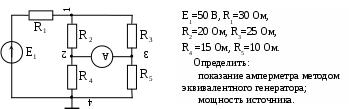 адача 1.3 адача 1.3Задача 1.4 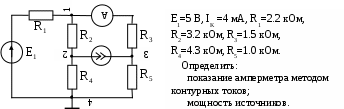 Задача 1.5 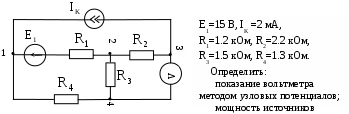 Задача 1.6 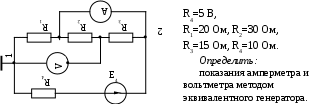 Задача 1.7 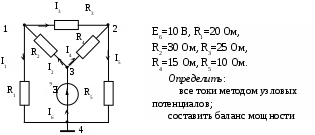 З 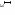 адача 1.8 адача 1.8  1 R3  2 IK5=0.5 A, IK6=0.1 A, R1=20 Oм, R2=30 Oм, R3=25 Oм, R4=15 Oм. Определить: все токи методом контурных токов; составить баланс мощности.      3  R4 R2      IK6 IK5        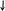 4    З 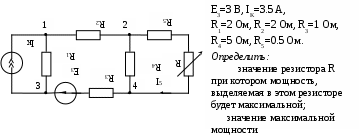 адача 1.9 адача 1.9Задача 1.10 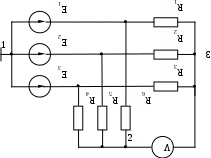 E1=5 B, E2=15 B, E3=20 B, R1=20 Oм, R2 =30 Oм, R3=15 Oм, R4 =45 Oм, R5=10 Oм, R6 =15 Oм. Определить: показание вольтметра методом узловых потенциалов Задача 1.11 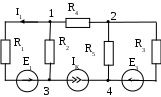 E1=12 В, E3=5.0 В, IK=0.02 А, R1=120 Ом, R2=150 Ом, R3=470 Ом, R4=150 Ом, R5=330 Ом. Определить: ток I1 методом наложения; 4. Рекомендации к выполнению задания 4.1. Законы Кирхгофа Как известно, для любой электрической цепи справедливы законы Кирхгофа для токов и напряжений. Первый закон Кирхгофа Алгебраическая сумма токов в проводниках, соединенных в узел, равна нулю Узлом в электрической цепи называется место соединения трёх и более ветвей, место соединения двух ветвей называется устранимым узлом. В (1.4.1) ток берется со знаком плюс, если ток втекает в узел, и со знаком минус, если вытекает. Ветвью называется участок цепи с последовательным соединением элементов, ветвь имеет только устранимые узлы, а ток во всех её элементах имеет одинаковое значение. Замкнутым контуром цепи называется путь по ветвям цепи, который начинается и заканчивается в одном и том же узле. Второй закон Кирхгофа Алгебраическая сумма напряжений на всех элементах замкнутого контура равна алгебраической сумме ЭДС всех источников того же контура 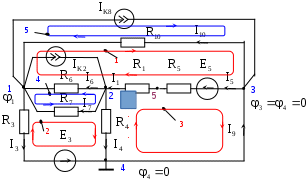 Рис. 3 Для составления уравнения необходимо задать направление обхода контура: по направлению часовой стрелки либо против часовой стрелки. В (1.4.2) ЭДС и напряжения берутся со знаком плюс, если их направления совпадают с направлением обхода контура, если не совпадают, то со знаком минус. Система независимых контуров составляется так, что в контур включаются только ветви с неизвестными токами, рекомендуется, чтобы ветвь входила в контур только один раз, а в каждый последующий контур должна входить хотя бы одна ветвь с неизвестным током, не вошедшая в предыдущие контуры. Для расчетов всех неизвестных токов в схеме составляется система уравнений Кирхгофа. По первому закону Кирхгофа составляется Так для схемы рис. 3 q = 4 (узел 5 устранимый и Для схемы рис. 3 составлены системы уравнений:  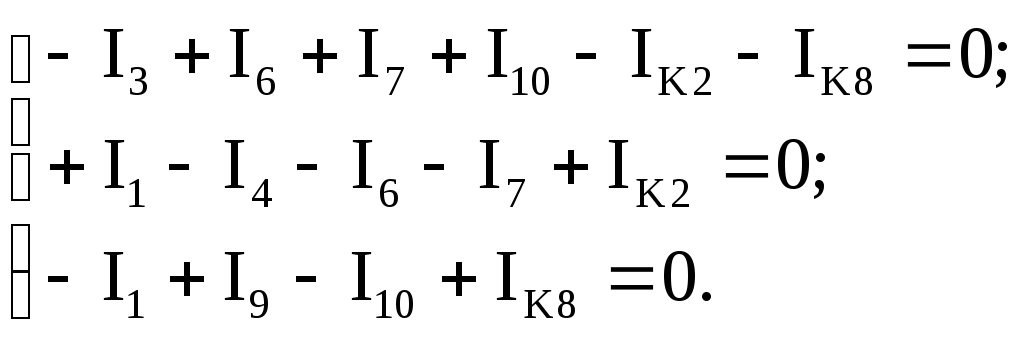 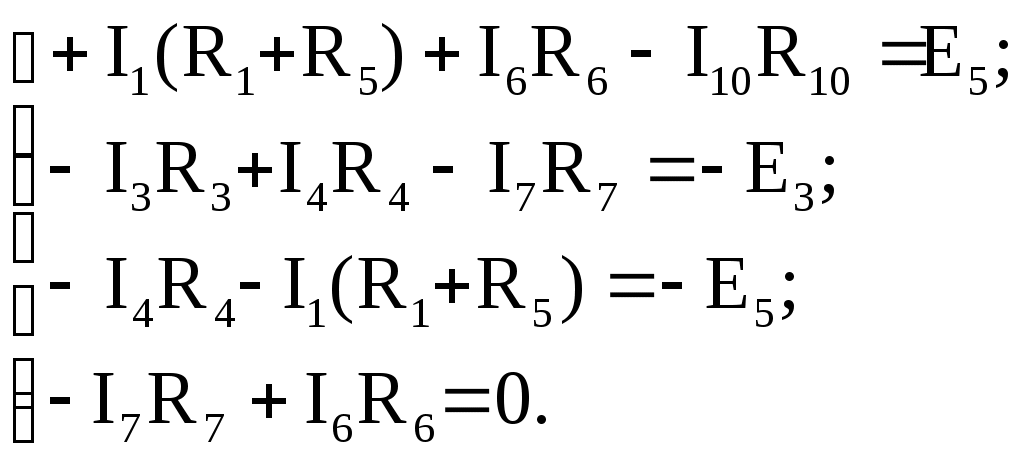 (3) (3)Решая систему уравнений (1.4.3), можно определить токи 4.2. Закона Ома для ветви с источниками ЭДС Для получения закона Ома для ветви с источниками ЭДС (рис. 4) воспользуемся вторым законом Кирхгофа, составленным для контура, образованного этой ветвью и напряжением между узлами, к которым она присоединена 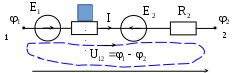 Рис. 4 Преобразуя уравнение (1.4), получим закон Ома для ветви с источниками ЭДС При определении тока I положительное направление напряжения 4.3. Метод узловых потенциалов Метод узловых потенциалов позволяет определить токи в ветвях схемы по закону Ома (5), исходя из предварительно найденных потенциалов узлов, причем потенциал одного из узлов задаётся нулевым, а для определения потенциалов остальных узлов составляется система уравнений: 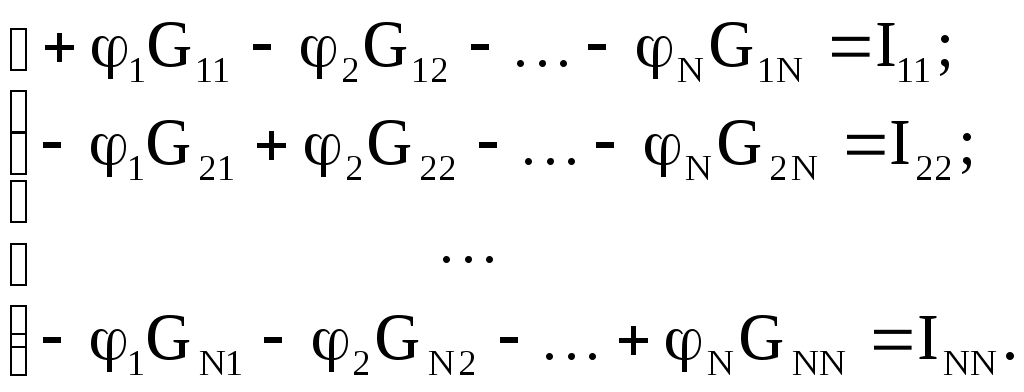 (6) (6)где Узловой ток где В (7) знак плюс ставится, если ЭДС или источник тока направлен к узлу j, а минус – от узла. Система уравнений общего вида (6), составленная для схемы рис. 4, представляется следующей системой уравнений для определения потенциалов 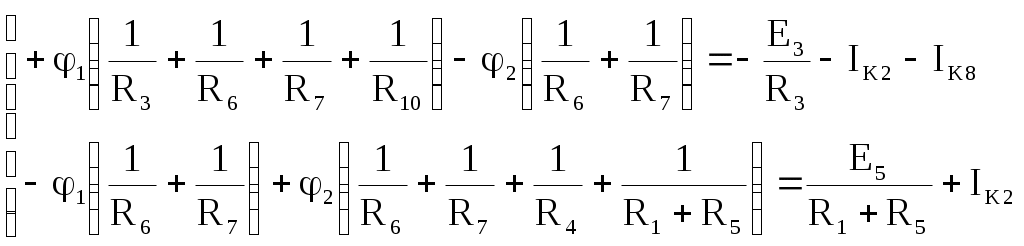 (8) (8)при этом Для определения токов составляются соотношения по закону Ома (5): 4.4. Метод контурных токов Метод позволяет определить токи в ветвях цепи, исходя из предварительно найденных промежуточных расчётных величин - контурных токов [1]. Полагается, что в каждом контуре протекает контурный ток. В качестве неизвестных (определяемых) полагаются контурные токи 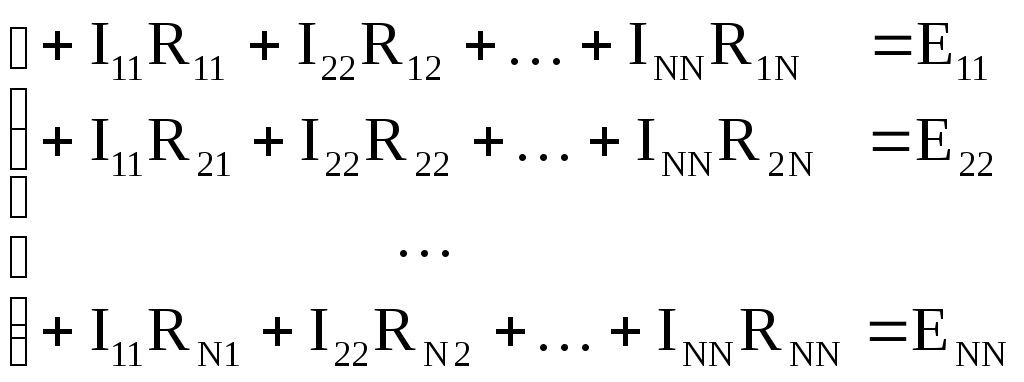 . (11) . (11)В (11): 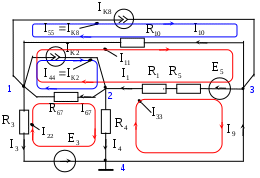 Рис. 5 Для учета источников тока в анализируемой цепи необходимо задать дополнительные контура, включающие ветви с источниками тока. Величина этих контурных токов равна токам источников тока. Рассмотрим пример рис. 3. В примере имеется две параллельных ветви с сопротивлениями 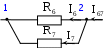 Расчетная схема приведена на рис 5. Система уравнений общего вида (11), составленная для схемы рис. 5, представляется следующей системой для определения контурных токов 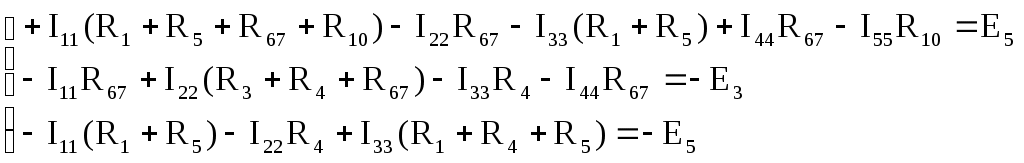 , (12) , (12)при этом Ток в конкретной ветви определяется как алгебраическая сумма контурных токов обтекающих соответствующую ветвь (рис. 5): Ток Токи 4.5. Баланс мощности Для любой электрической цепи алгебраическая сумма мощностей отдаваемых источниками равна сумме мощностей потребителей [1]: где мощность источников мощность потребителей. Знак «+» или «-» у мощности источников зависит от направления напряжения и тока на источнике рис. 6. 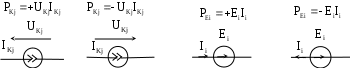 Рис. 6 В качестве примера рассмотрим схему, приведенную на рис. 3. Составим баланс мощности 4.6. Метод наложения Для линейных цепей любой ток или напряжение на участке цепи могут быть определены суммой составляющих, рассчитанных отдельно от действия каждого и 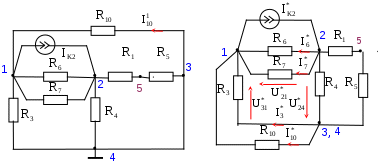 сточника или групп источников [1]. Такое свойство линейных цепей называется принципом суперпозиций или принципом наложения. сточника или групп источников [1]. Такое свойство линейных цепей называется принципом суперпозиций или принципом наложения.Рис. 7 Рис. 8 В качестве примера рассмотрим схему, приведенную на рис. 3. Определим ток где составляющая На рис. 7 изображена схема для определения составляющей от действия источника тока - Составляющую Зададим ток в дальней ветви Найдём коэффициент пропорционального пересчёта Истинная составляющая тока Схема для определения составляющей - 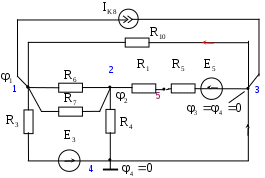 Рис. 9 Для определения тока 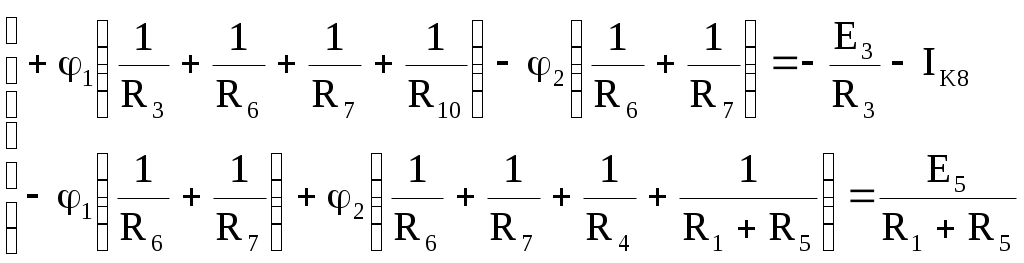 (18) (18)при этом 4.7. Метод эквивалентного генератора В методе эквивалентного генератора используется теорема об эквивалентном генераторе [1]. В соответствии с этой теоремой любая линейная цепь относительно выбранной ветви может быть представлена эквивалентным источником ЭДС - 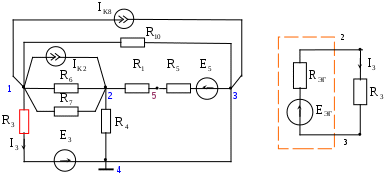 а б Рис. 10 ЭДС генератора - В качестве примера рассмотрим схему рис 10,а, где определим ток в сопротивлении ЭДС эквивалентного генератора можно определить, например, по методу узловых потенциалов. Для схемы рис. 11, а, как 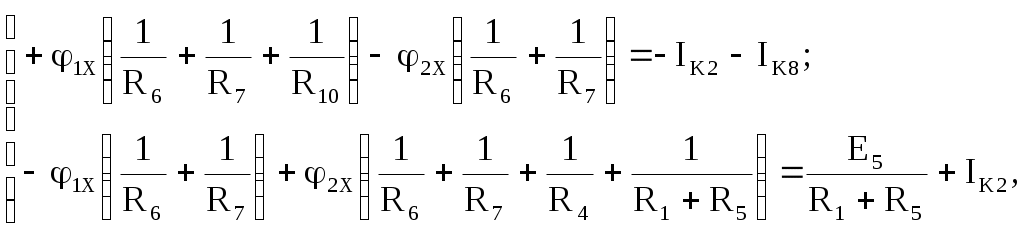 (20) (20)при этом 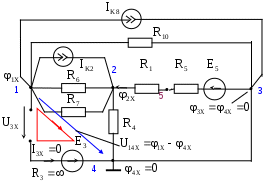 Рис. 11 Для определения напряжения 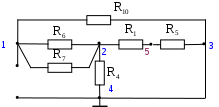 Рис. 12 Сопротивление эквивалентного генератора можно определить как входное сопротивление Окончательно можно определить ток 4.8. Основные определения теории графов |
