РГЗ тоэ. Новосибирский государственный технический университет
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
Теория графов – раздел математики, имеющий множество инженерных и вычислительных приложений, применение которого позволило разработать машинные методы расчета и проектирования электрических цепей. Теория графов позволяет определить общие свойства цепей, рассматривая только структуру (топологию) цепи. Топология электрической цепи характеризуется двумя основными понятиями: ветвью и узлом. Ветвьюэлектрической цепи называют ее участок, имеющий два вывода, через которые цепь взаимодействует с остальной частью цепи. Ветвь может быть двухполюсным элементом, однако для уменьшения числа переменных часто под ветвью понимают участки цепи, имеющие одно и то же значение тока или одно и то же значение напряжения, т. е. участки цепи с последовательным или параллельным соединением двухполюсных элементов. Узлом в электрической цепи называется место соединения двух и более ветвей, место соединения двух ветвей называется простым или устранимым узлом. Узел, который содержит хотя бы одну ветвь, не входящую в другие узлы, называют независимым. Состояниецепи характеризуется токами и напряжениями ветвей. При анализе электрической цепи обычно полагают, что определению подлежат токи и напряжения ветвей при условии, что параметры всех элементов цепи известны. 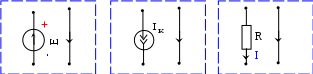 Рис. 13 При изучении топологических свойств электрической цепи содержание ветвей не имеет значения, поэтому ветви (резистор, источники ЭДС и тока, индуктивность, ёмкость и любой двухполюсный элемент) изображают отрезками линий, называемыми ветвями графа, включенных между узлами. Совокупность узлов соединённых ветвями (линиями) называют топологическимили структурным графом электрической цепи. 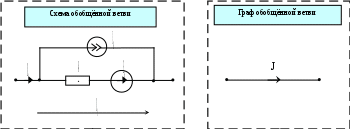 Рис. 14. Каждой ветви можно задать направление. Полагается, что для любой ветви, за исключением источников, направление ветви совпадает с направлением протекающего через элемент тока и указывает на то, что узел, из которого вытекает ток, имеет более высокий потенциал, чем узел, в который ток втекает. Поскольку потенциалы узлов цепи до решения системы уравнений неизвестны, направление ветвей графа, соответствующих пассивным элементам, полностью произвольно. Для источников ЭДС примем направление ветви графа от положительного к отрицательному полюсу источника (рис. 13). 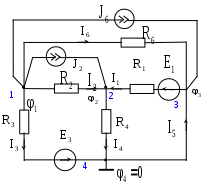 Рис. 15. Для получения уравнений, описывающих режим работы цепи, удобно использовать обобщенную ветвь (рис. 14). Граф, состоящий из направленных ветвей, называется сигнальным или направленным графом. Для проведения анализа цепи с помощью теории графов в исходной цепи (рис. 2.) целесообразно провести элементарные преобразования – параллельное соединение 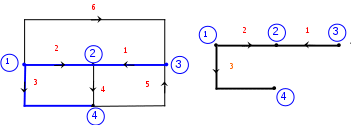 Рис. 16. Рис. 17. подграф - любая часть графа электрической цепи; путь графа - подграф образованный непрерывной последовательностью ветвей, связывающий выбранную пару ветвей; связный граф - граф, в котором меду любой парой выбранных узлов существует путь; контур - путь по ветвям графа, который начинается и заканчивается в одном и том же узле, причём каждый узел входит в контур только один раз; дерево - связный подграф графа цепи, включающий в себя все узлы графа, но не содержащий замкнутых контуров; рёбра - ветви входящие в состав дерева графа; хорды иливетви связи - ветви графа не вошедшие в состав дерева; независимый контур- контур, который содержит хотя бы одну ветвь, не входящую в другие контуры, причём независимый контур образуется всякий раз, когда к дереву графа добавляется хорда; главный контур - контур, который образован ветвями дерева и только одной хордой. На рис. 5 изображено дерево графа (рис. 5), которое, получено удалением ветвей 4, 5 и 6, которые являются хордами. Пусть q – число неустранимых узлов в схеме и р - число ветвей с неизвестными токами цепи. Тогда: n=q-1 — число ветвей дерева, которое равно числу независимых узлов, поскольку первая ветвь дерева содержит два узла, а каждая последующая ветвь вводит только один новый узел; m=p-q+1 — число ветвей связи, которое равно числу главных (независимых) контуров. Если определению подлежат токи всех ветвей, то число неизвестных уравнений системы равно числу ветвей с неизвестными токами графа – p = n+m. Так для схемы рис. 2 q = 4 (узел 5 устранимый и Топологическая структура цепи описывается с помощью специальных матриц, которые определяют взаимные связи ветвей с узлами и контурами графа. Основными из них являются: Узловая матрица - А; Контурная матрица - В; Матрица сечений - Q, 4.9. Получение топологических матриц 4.9.1. [А] – узловая матрица [А] - узловая матрица или матрица инциденций представляет собой таблицу, строки которой соответствуют узлам графа, а столбцы — его ветвям. Элементы матрицы имеют следующие значения: + 1- если ветвь i связана с узлом jи направлена от узла; − 1- если ветвь i связана с узлом j инаправлена от узла; 0- если же ветвь i не связана с узлом j. Таким образом, элементы строки показывают, какие ветви входят в узел или выходят из него. Таблица 2.
Узловая матрица, составленная для всех узлов цепи, называется неопределенной. Сумма элементов любого столбца такой матрицы равна нулю. Если узловая матрица составлена только для независимых узлов, то она называется определенной. При этом один из узлов графа считают базисным или опорным, и он не входит в матрицу. По известной узловой матрице можно построить граф цепи. Определенная узловая матрица [A], составленная для графа, изображенного на рис. 16, при условии, что узел 4 принят за базисный, имеет вид: 4.9.2. [Q] - матрица главных сечений Сечением называют замкнутую поверхность, охватывающую часть графа электрической цепи. Сечение графа является обобщением понятия узла. На чертеже сечение изображают в виде следа этой поверхности, рассекающей граф на две части. Тем самым сечение графа делит его на два изолированных подграфа. 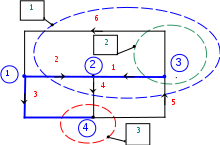 Рис. 18. Пример узлов и сечений графа Сечение называют независимым или главным, если оно содержит ветви связи и только одну ветвь дерева. Следовательно, каждая ветвь дерева позволяет построить только одно независимое сечение, поэтому полное число главных сечений равно n = q - 1 — числу ветвей дерева На рис. 18 изображен граф электрической цепи, содержащий дерево с ветвями 1, 2, 3 и ветви связи 4, 5, 6. Пунктирными линиями на графе нанесены сечения. Каждое сечение содержит только одну ветвь дерева и, следовательно, является независимым. [Q] - матрицей сечений представляет собой таблицу, строки которой соответствуют сечениям графа, а столбцы — его ветвям. Элементы матрицы имеют следующие значения: + 1- если ветвь i входит в сечение j; − 1- если ветвь i выходит из сечения j; 0 − если же ветвь i не связана с сечением j. Таким образом, элементы строки показывают, какие ветви входят в сечение или выходят из него. Матрица сечений [Q], построенная для графа, изображенного на рис.16, имеет вид Таблица 3.
4.9.3. [B] - матрица главных контуров Контурная матрица - [B] представляет собой таблицу, строки которой соответствуют контурам графа, а столбцы − его ветвям. Элементы матрицы имеют следующие значения: +1 если контур iсодержит ветвьjи направление обхода контура совпадает с направлением ветви; −1 если контурi содержит ветвь j и направление обхода контура противоположно направлению ветви; 0 если же контур i не содержит ветви j. Таким образом, элементы строки матрицы [В] показывают, какие ветви входят в контуры и как они направлены. Контурная матрица может быть составлена как для всех контуров цепи, так и для независимых контуров. Если контурную матрицу составляют для всех контуров цепи, то ее называют неопределенной. При этом один из контуров считают базисным или опорным, и он не входит в матрицу [В]. Полное число контуров определяют из условия, что каждая ветвь графа входит в два противоположно направленных контура. Независимая система контуров составляется так, чтобы в каждый контур входили ветви дерева графа и одна из хорд. Число главных (независимых) контуров, которое равно числу хорд можно определить как Если контурная матрица составлена только для независимых контуров, то ее называют определенной. По известной контурной матрице можно построить граф цепи. 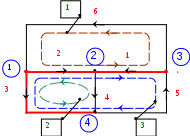 Рис. 19 Определенная контурная матрица, составленная для графа рис. 19, имеет вид Таблица 4.
4.10. Формирование уравнений в матричной форме: 4.10.1. Формирование уравнений Кирхгофа в матричной форме Законы Кирхгофа для токов (1) и напряжений (2) имеют универсальный характер и справедливы при любых видах воздействий и любых элементах, включенных в ветви цепи, как линейных, так и нелинейных. Т 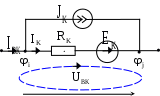 ак как вид уравнений Кирхгофа зависят лишь от способа соединения элементов схемы друг с другом, т. е. от топологии схемы, то их принято называть топологическими. ак как вид уравнений Кирхгофа зависят лишь от способа соединения элементов схемы друг с другом, т. е. от топологии схемы, то их принято называть топологическими.Рис. 20. Уравнения Кирхгофа можно записать в матричной форме, используя топологические матрицы: узловые, сечений и контурные. Для этого токи ветвей (рис. 20) 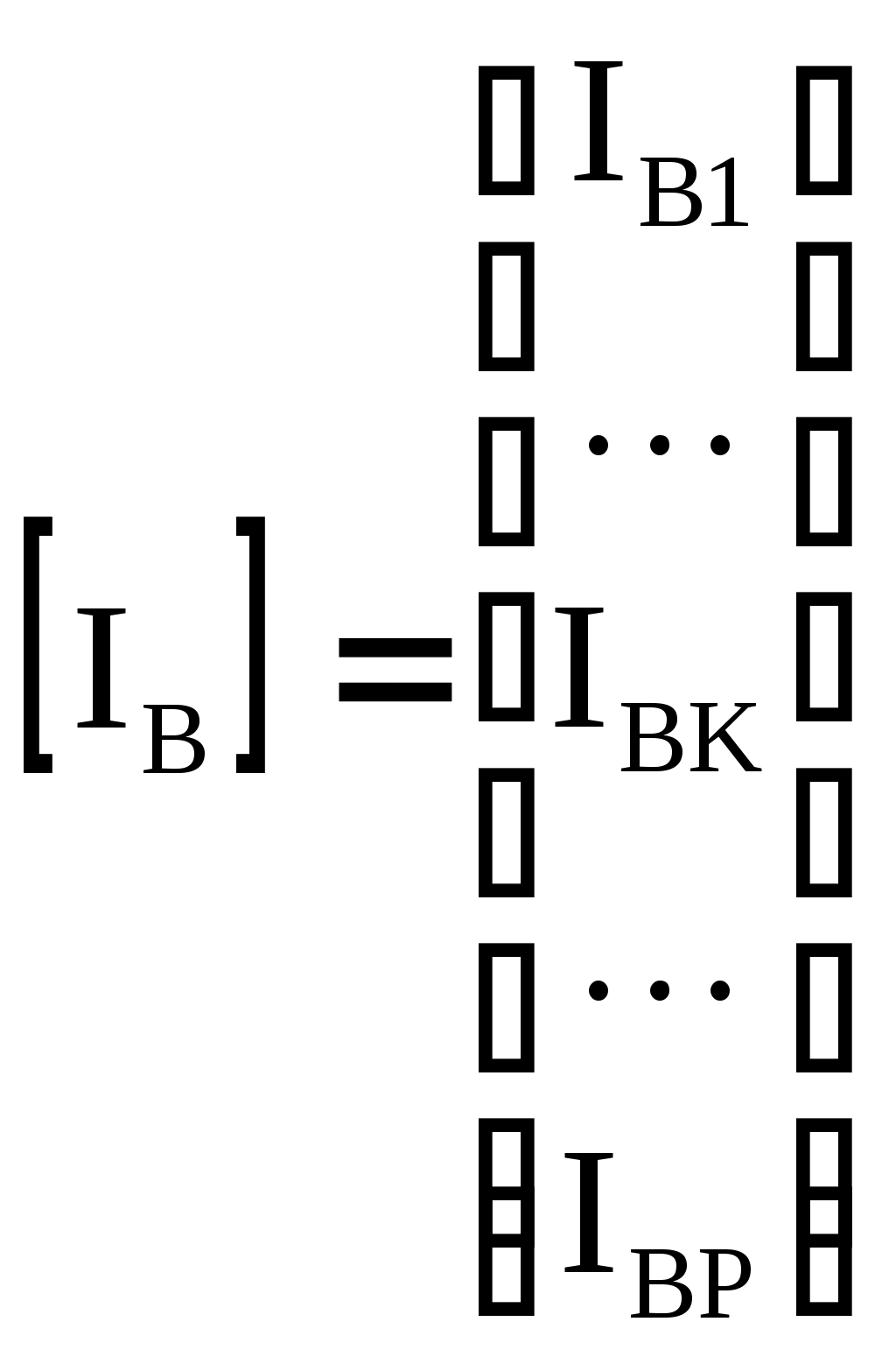 ; ; 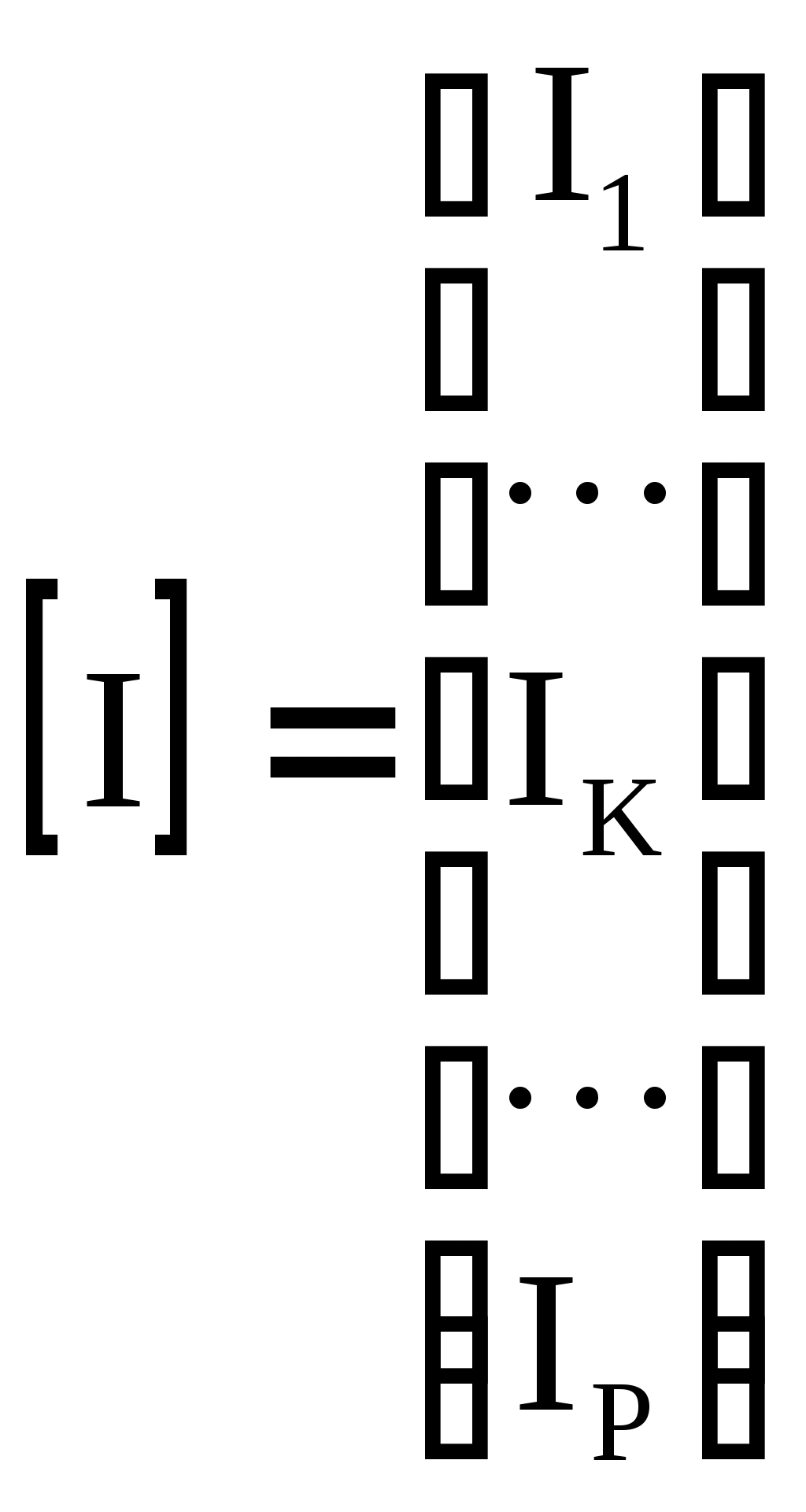 ; ; 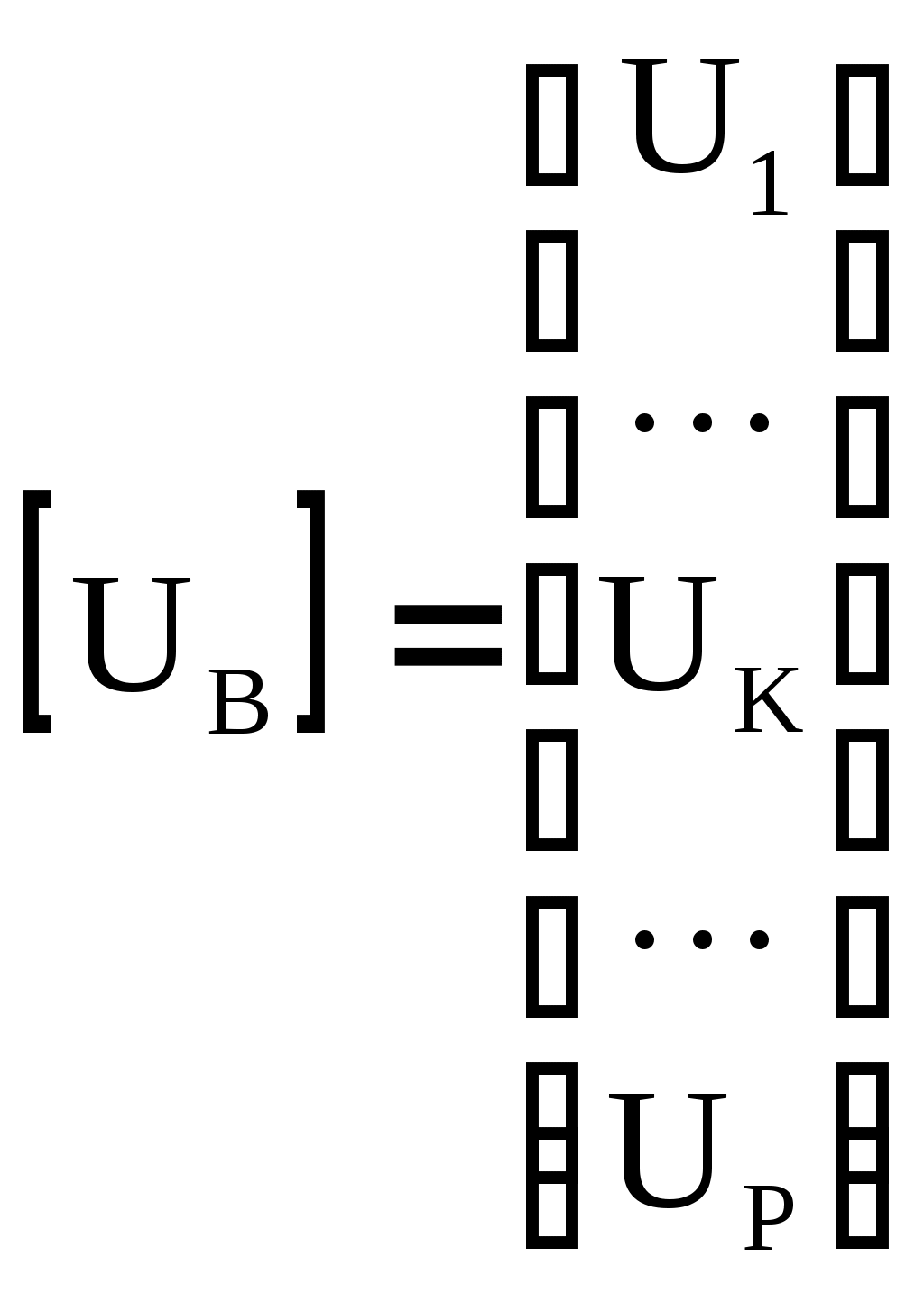 ; ; 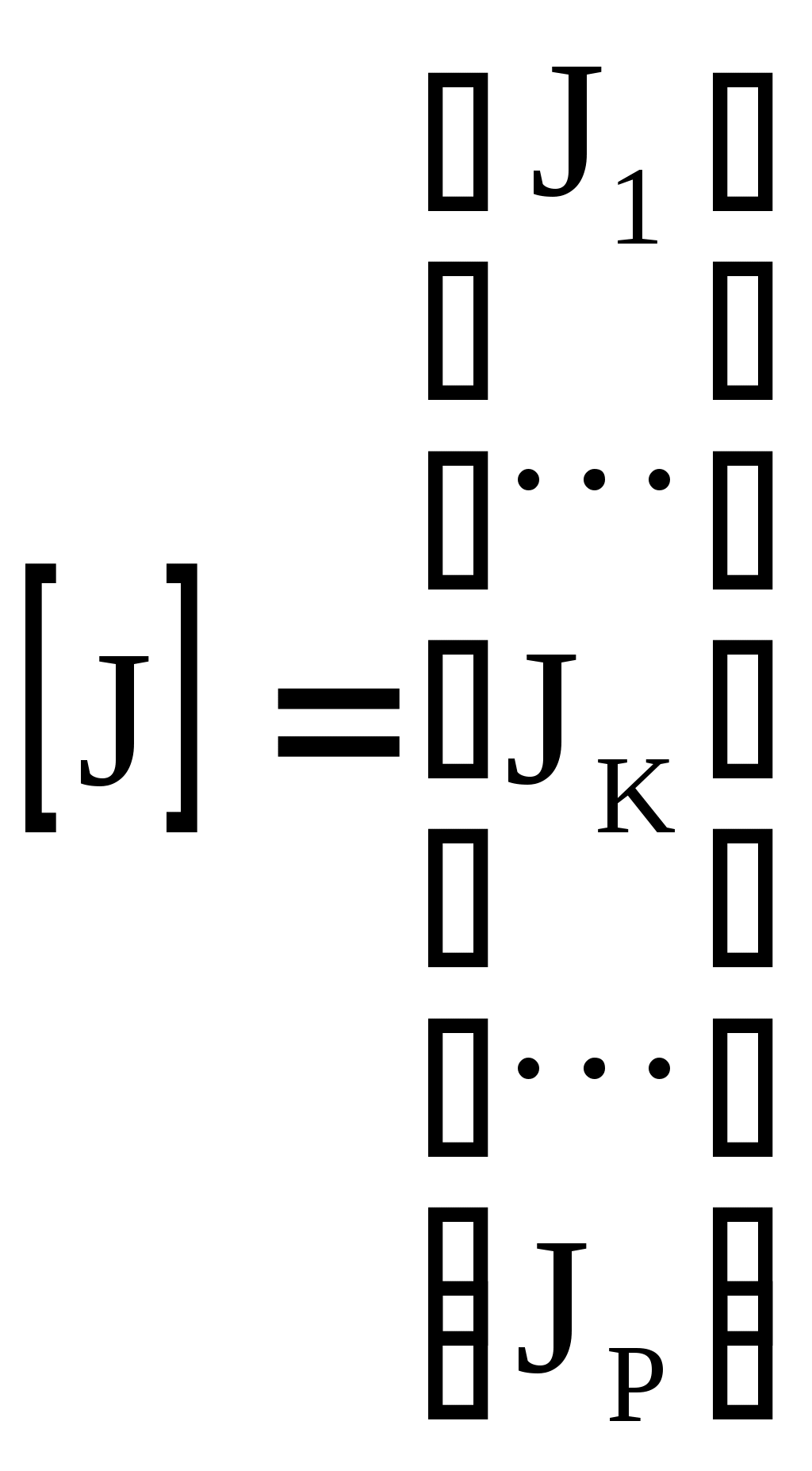 ; ; 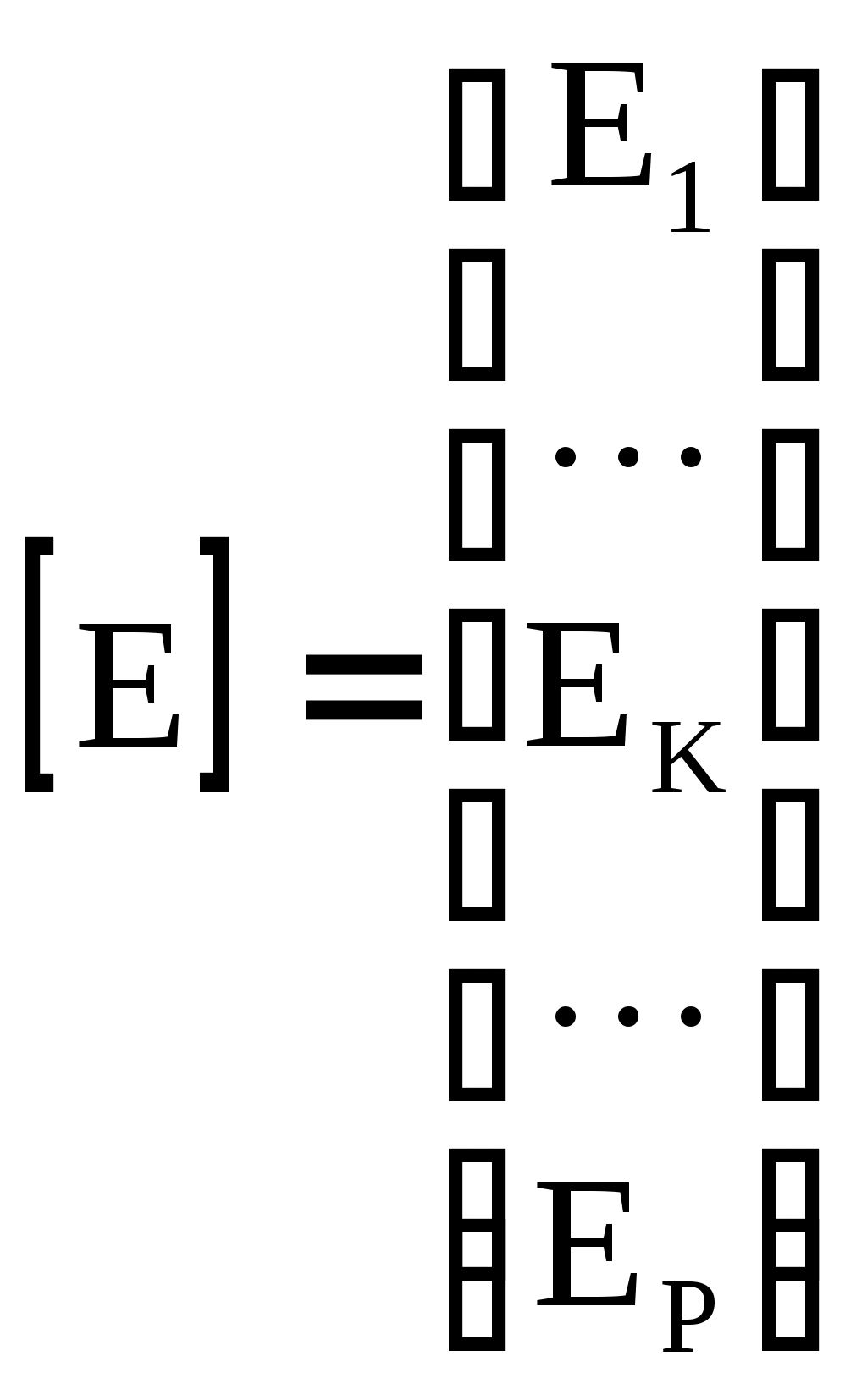 . (25) . (25)Сопротивления ветвей 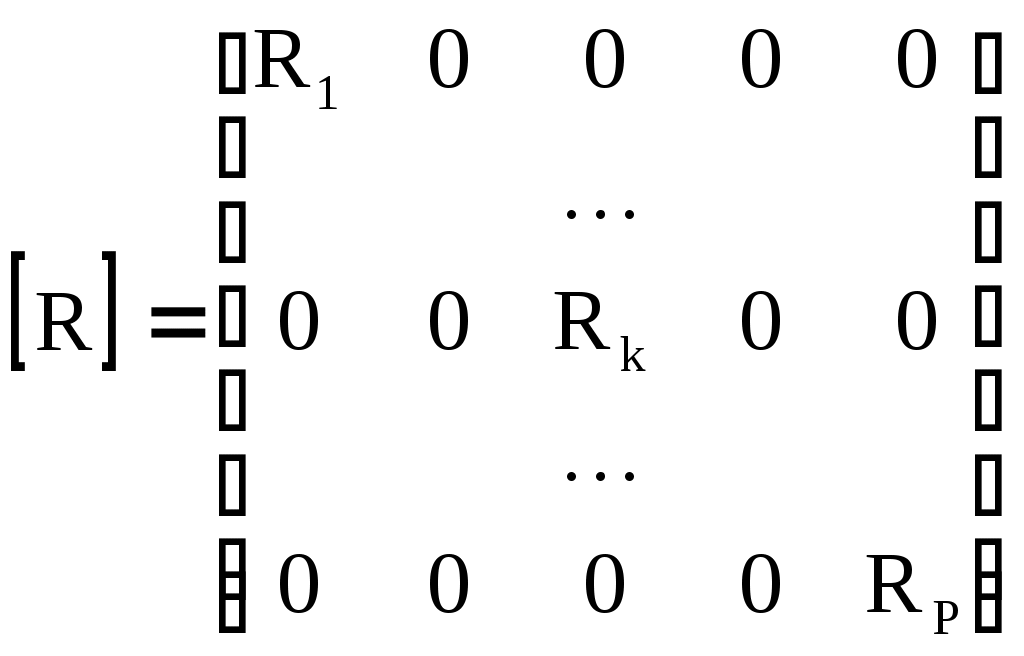 (26) (26)Так как элементы строки узловой матрицы [А] содержат сведения о ветвях, связанных с узлами цепи, и отражают направления токов в этих узлах, то сумма произведений элементов каждой строки на токи соответствующих ветвей представляет собой первый закон Кирхгофа ( [А][IВ]=0 (27) Определим токи в резисторах для обобщенных ветвей (рис. 1): [IВ]=[I]+[J] (28) Подставив (28) в (27) получим первый закон Кирхгофа в матричной форме: [А][I]= − [А][J] (29) При составлении (29) учитывалось, что произведение прямоугольной матрицы [А] на матрицу столбец [J] дает также матрицу столбец, элементы которой равны сумме произведений элементов строки матрицы [А] на элементы столбца матрицы [I]. Для обобщенных узлов, какими являются сечения, можно записать первый закон Кирхгофа, аналогичный уравнению (27): [Q][I]= − [Q][J]. (30) В (33) учитывается, что алгебраическая сумма токов в любом сечении электрической цепи равна нулю, а узел рассматривается как частный случай сечения [Q] = [A]. Аналогично может быть представлен второй закон Кирхгофа ( [B][UB]=0. (31) Напряжение ветви рис. 20 можно определить через напряжение на резисторе и э. д. с. ветви: [UB]=[I][R] − [E]. (32) Подставив (8) в (7) получим второй закон Кирхгофа: [B][R][I]=[B][E] или [RЗК] [I]=[B][E]. (33) Так как элементы строки матрицы [В] содержат сведения о ветвях, связанных с контурами цепи, и отражают направления напряжений на этих ветвях, уравнения (30) и (33) представляют собой уравнения Кирхгофа в матричной форме (34). Произведение [B][R]=[RЗК] является матрицей сопротивлений второго закона Кирхгофа. Окончательно система уравнений, составленная по первому и второму законам Кирхгофа, представляется блочной матрицей: 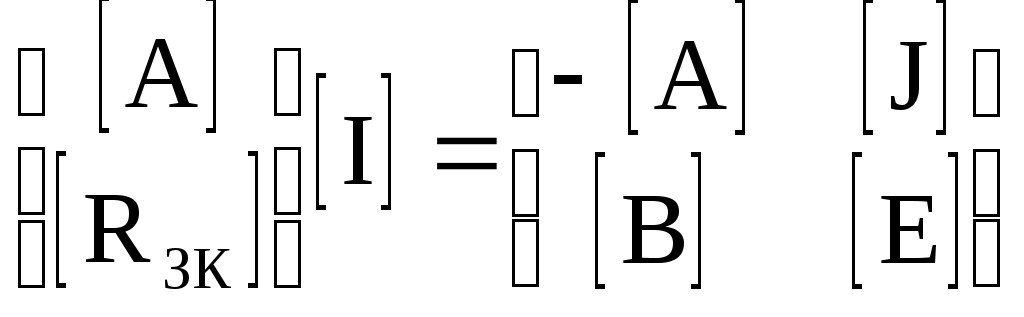 . (34) . (34)Рассмотрим пример рис. 15. Если определению подлежат токи всех ветвей, то число неизвестных уравнений системы равно числу ветвей с неизвестными токами графа – p = 6 (q = 4- число узлов, n = q − 1 = 3 − число независимых узлов и m = p − q +1 = 3 – число независимых контуров). 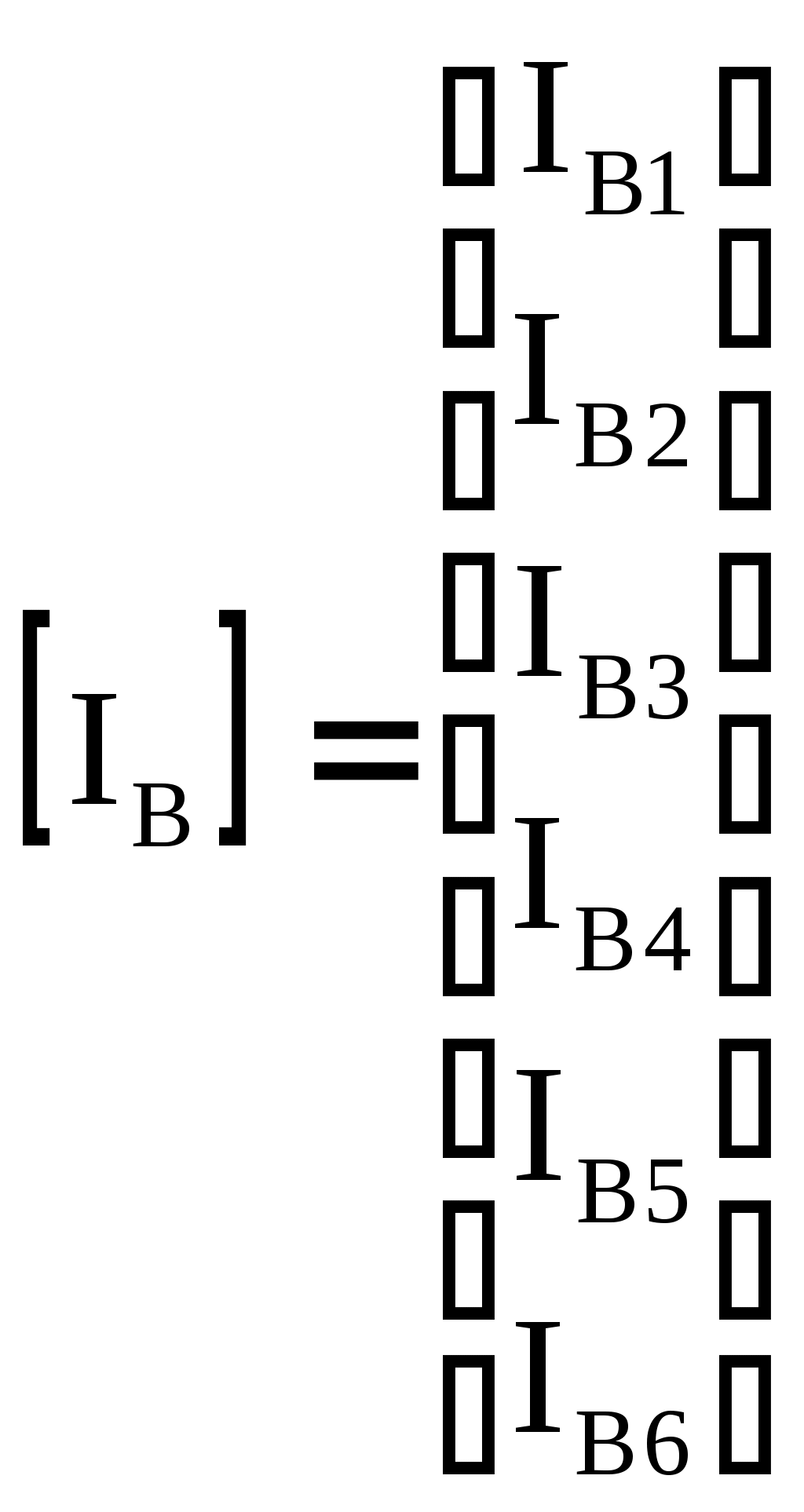 ; ; 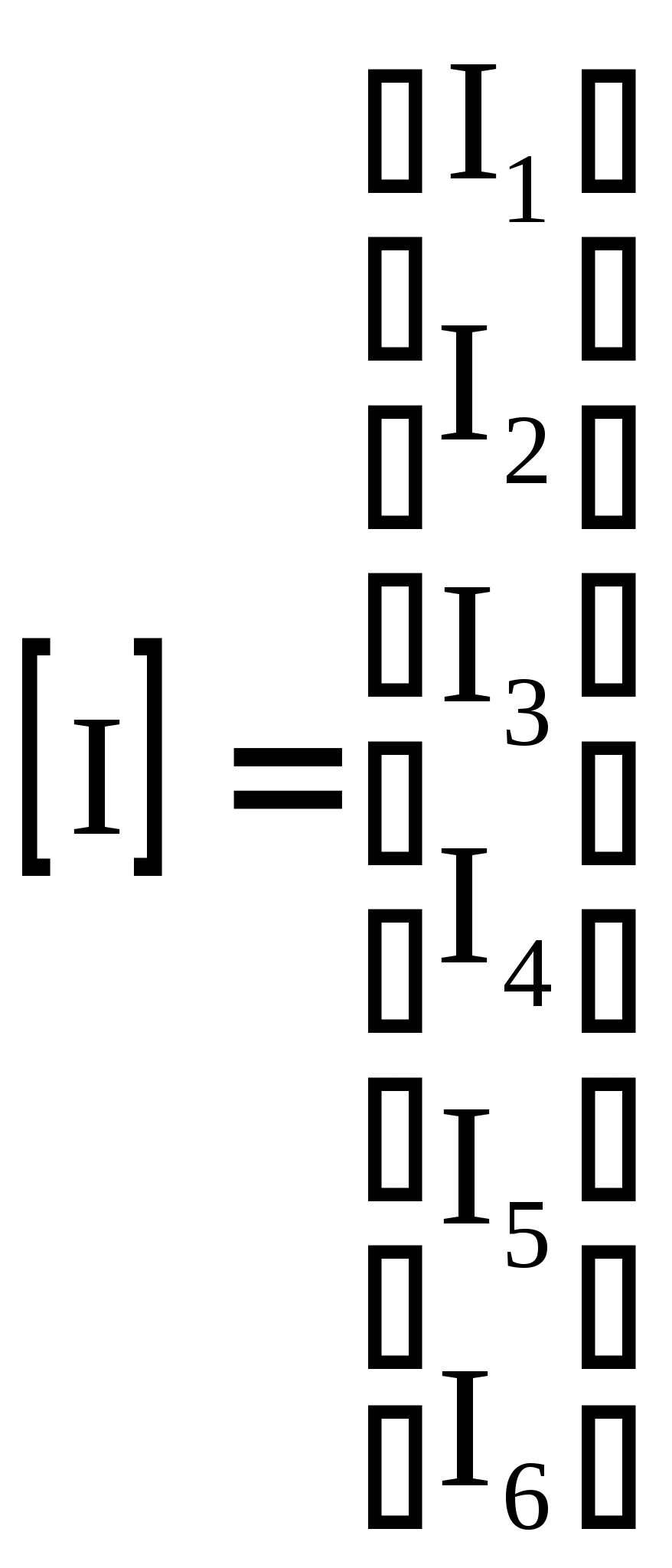 ; ; 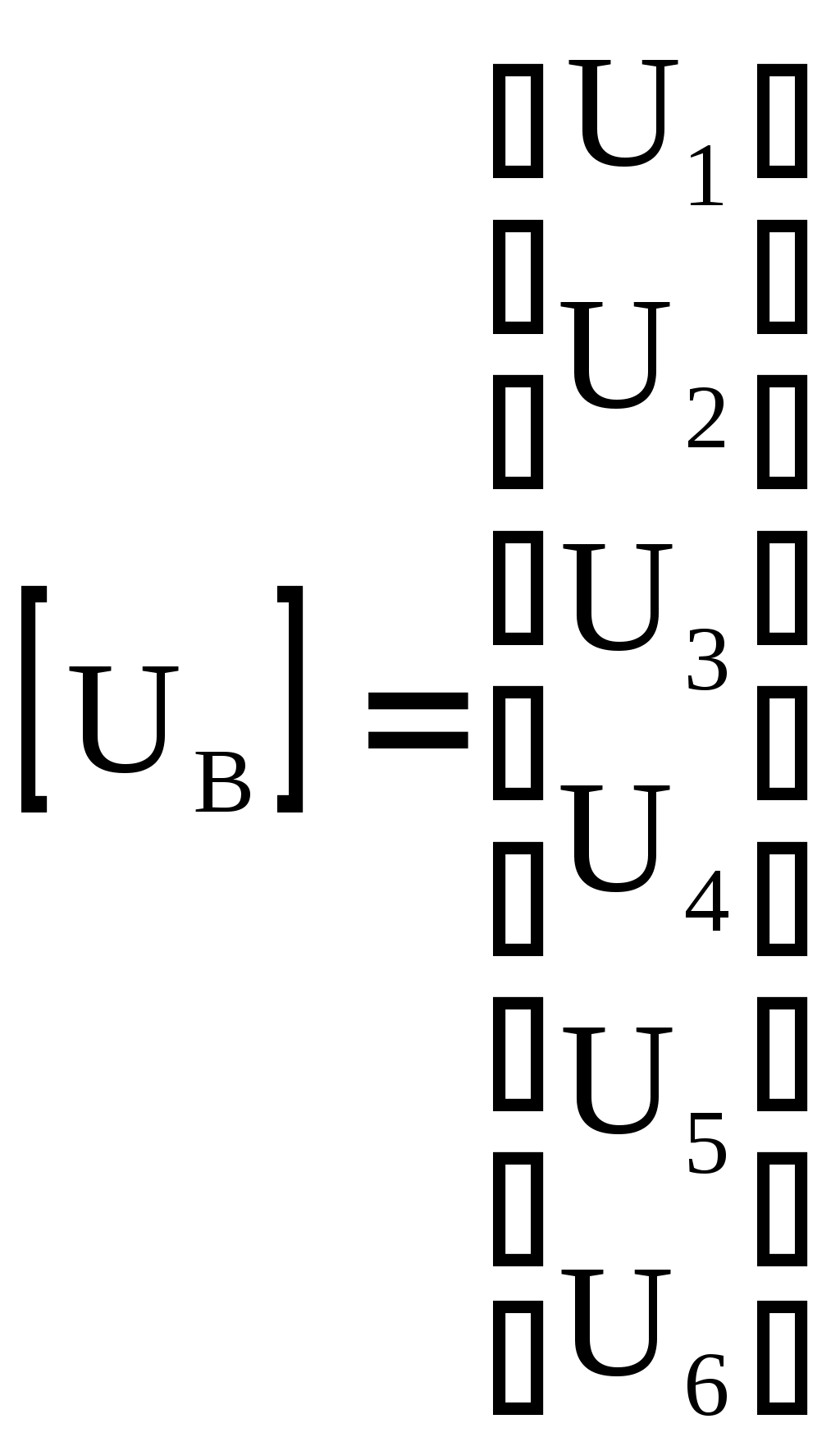 ; ; 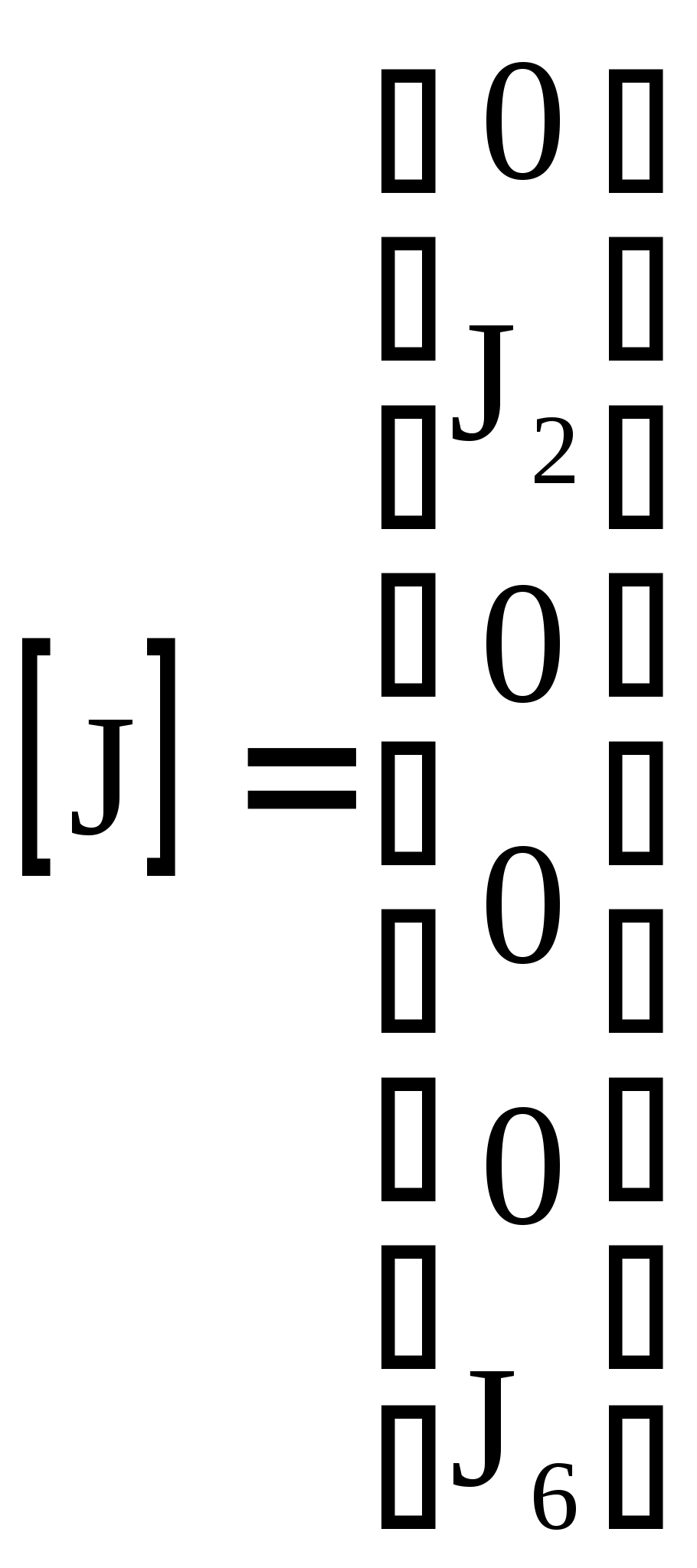 ; ; 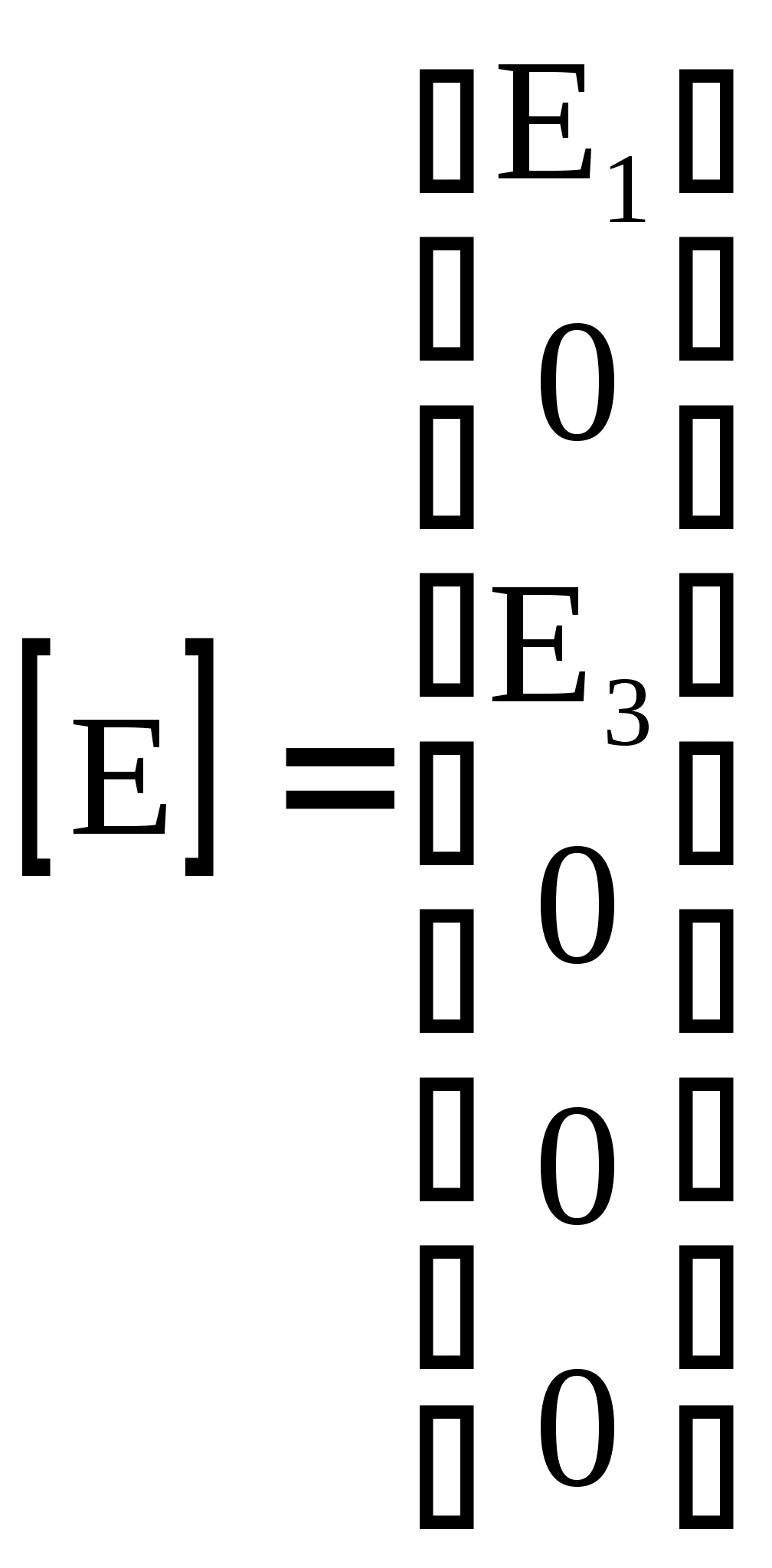 . (35) . (35)Сопротивления ветвей 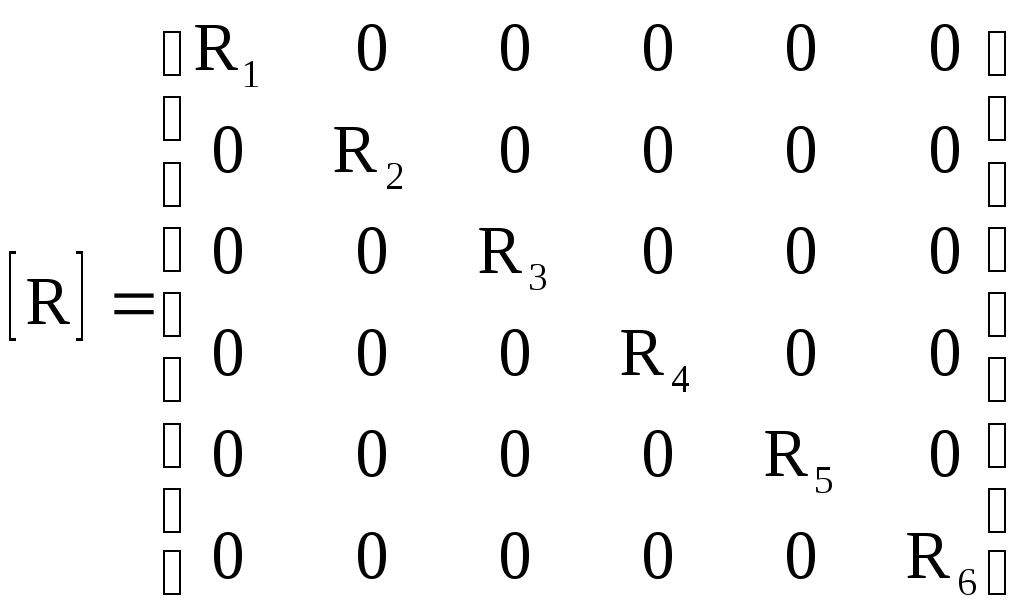 . (36) . (36)Определенная узловая матрица [A], составленная для графа, изображенного на рис. 19, при условии, что узел 4 принят за базисный, имеет вид (табл. 2): 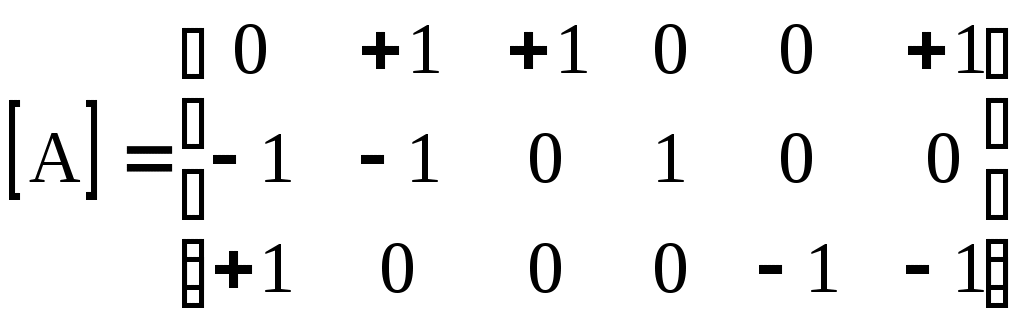 . (37) . (37)Определенная контурная матрица[B], составленная для графа рис. 19, имеет вид (табл. 4): 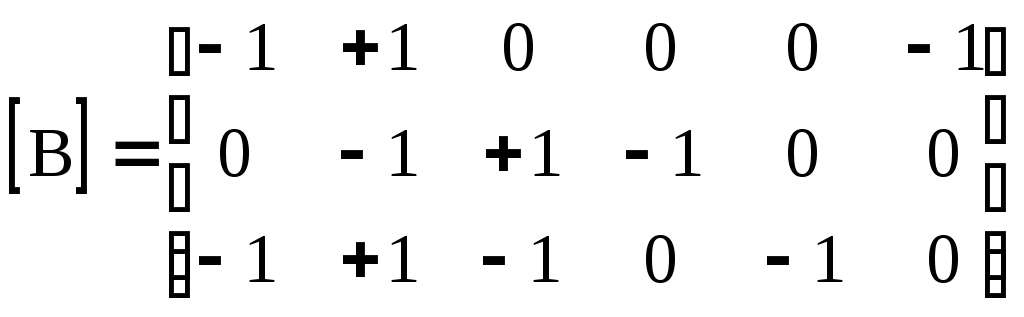 . (38) . (38)Матрица сопротивлений второго закона Кирхгофа [RЗК] 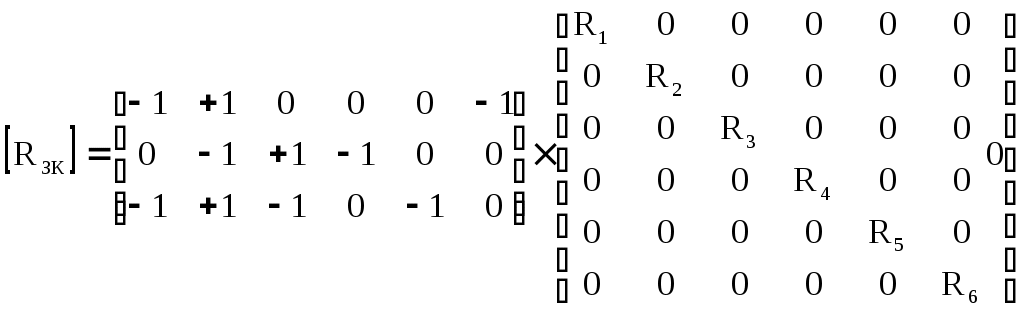 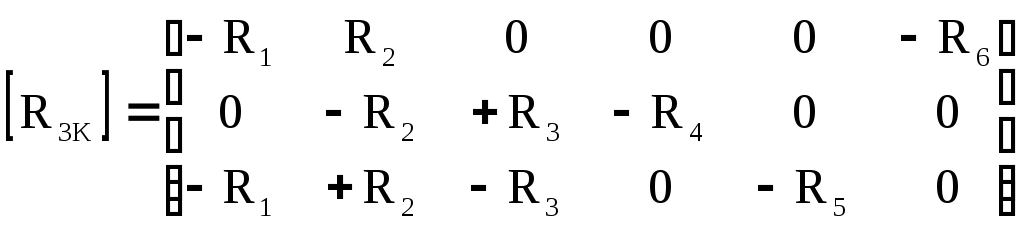 . (39) . (39)Матрица источников тока первого закона Кирхгофа 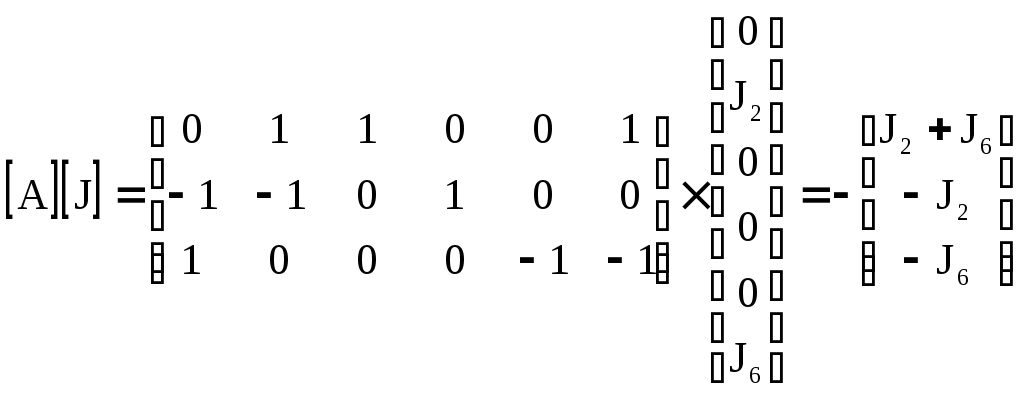 . (40) . (40)Матрица э. д. с. контуров второго закона Кирхгофа 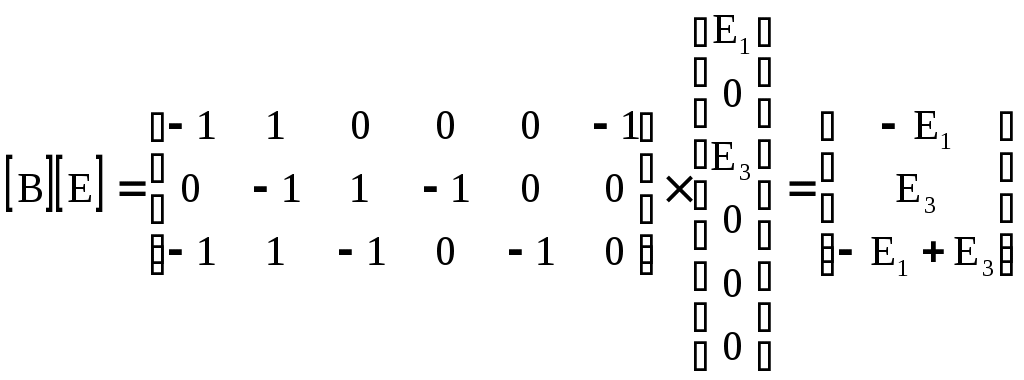 . (41) . (41)Итоговая система уравнений Кирхгофа в матричной форме: 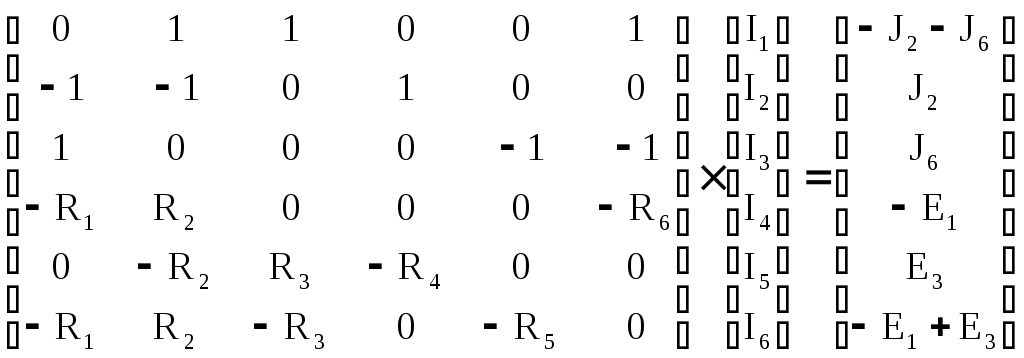 . (42) . (42)4.10.2. Формирование уравнений узловых потенциалов в матричной форме Узловое потенциалы φопределяется как напряжение между i-м независимым и базисным узлами цепи. Для упрощения расчётов потенциал базисного узла полагается равным нулю. Число узловых потенциалов равно числу независимых узлов цепи. Столбцы узловой матрицы [А] содержат информацию о том, между какими узлами включена k-я ветвь и как она направлена (рис. 1). Если умножить элементы транспонированной матрицы [AT] на соответствующие узловые потенциалы и сложить составляющие, то в результате получатся напряжения на отдельных ветвях. Вывод уравнений узловых потенциалов. Представим узловые потенциалы цепи в виде матрицы столбца: 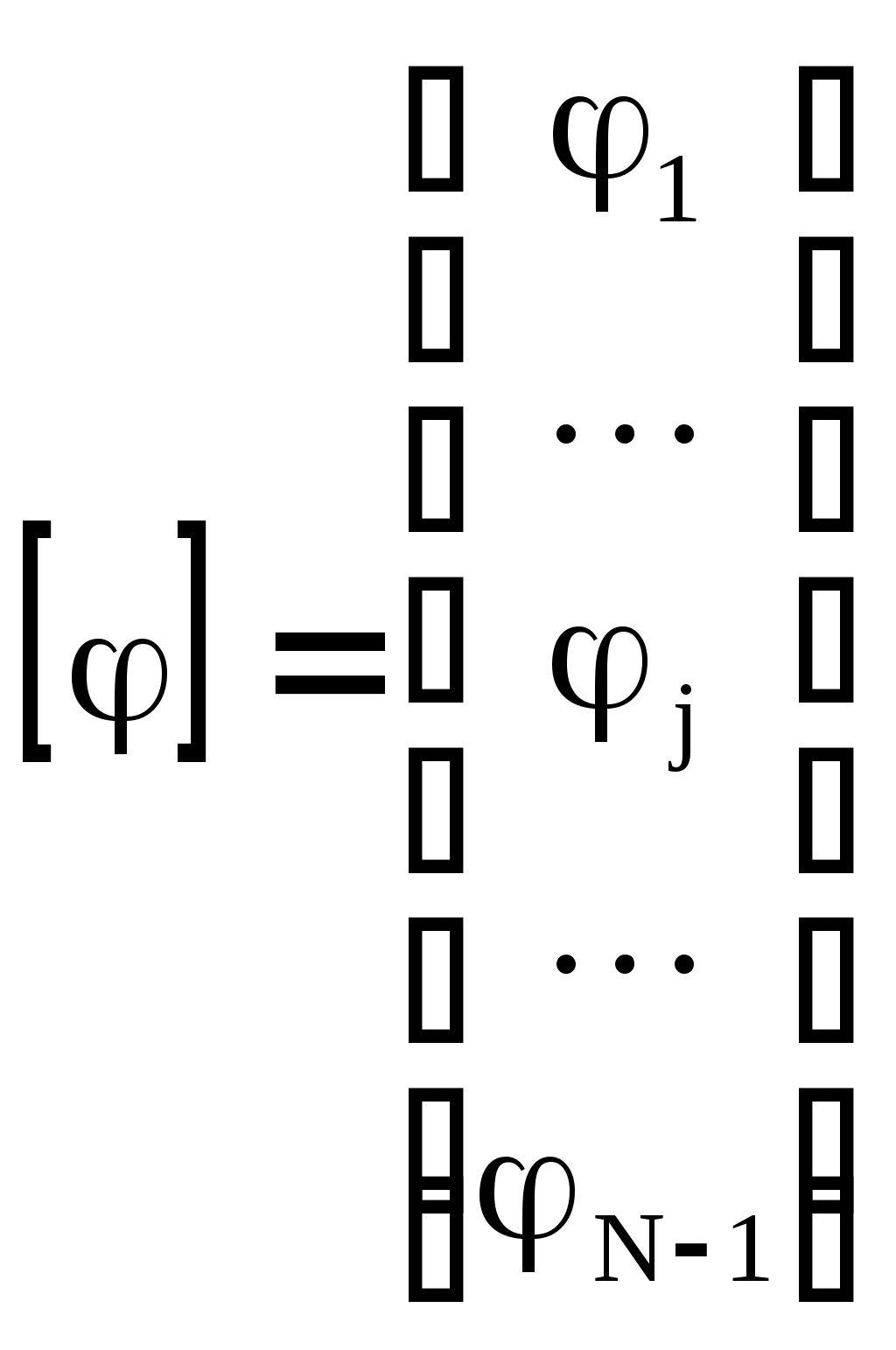 . (43) . (43)Тогда, умножая транспонированную узловую матрицу [AT] (т. е. матрицу [А], в которой строки заменены столбцами) на матрицу узловых напряжений, получим напряжения на ветвях: [AT] [φ] = [UB]. (44) Для обобщённой ветви (рис. 20) токи в резисторах определим по первому закону Кирхгофа: [I] = [IB] − [J]. (45) По второму закону Кирхгофа определим напряжения на резисторах через разницу потенциалов узлов, к которым присоединена ветвь: [R] [I] – [UB]= [E]. (46) Из (4) определим токи в резисторах [I] = [R] -1 [[E] + [UB]]. (47) Обозначим [G] = [R] -1 − матрица проводимостей 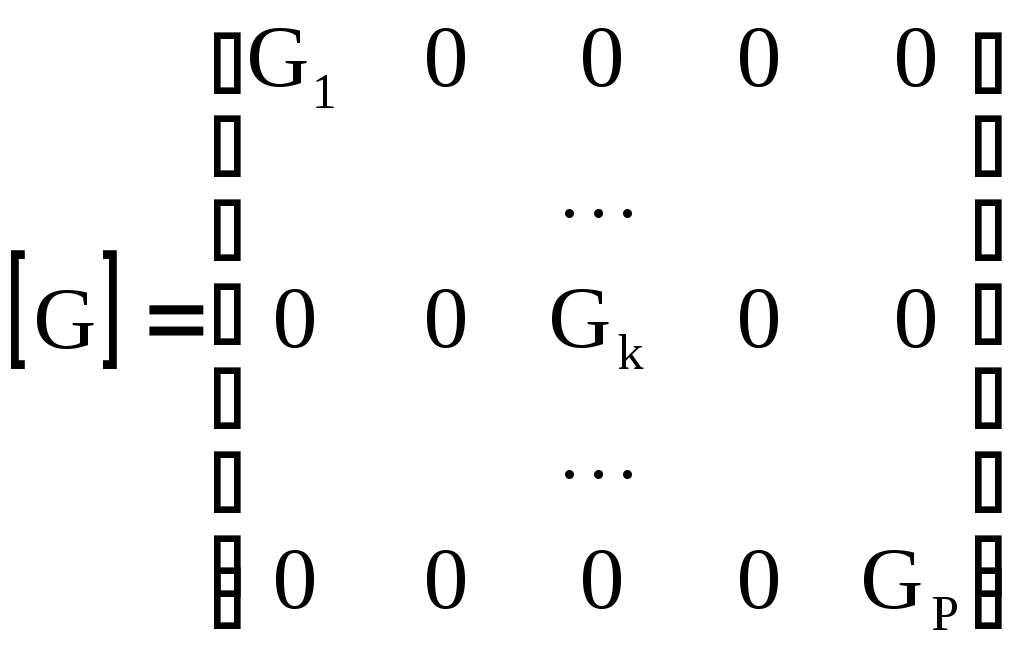 . (48) . (48)где Gk = 1\ RК. Из (45) и (47) определим токи в ветвях [IB] - [J] = [G] [E] + [G] [UB] . (49) Умножим (49) на [A] и учтём, что [A] [IB] = 0 [A] [G] [UB] = − [A] [ [G] [E] + [J] ]. (50) С учётом (44) получим: [A] [G] [AT] [φ] = − [A] [ [J]+[G] [E] ]. (51) В (51) обозначим: [GУП] = [A] [G] [AT]. (52) и [JУП] = − [A] [ [J]+[G] [E] ]. (53) матрицы узловых проводимостей и узловых токов метода узловых потенциалов. Окончательно получим уравнение метода узловых потенциалов: [GУП] [φ] = [JУП]. (54) Токи обобщённой ветви (рис. 20) в резисторах определим по закону Ома после определения потенциалов узлов, который можно получить из (46) с учётом (44): [I] = [G] [[E] + [AT] [φ]]. (55) Рассмотрим пример рис. 15 формирования уравнений узловых потенциалов в матричной форме. Пусть определению подлежат токи всех ветвей после расчёта потенциалов узлов Число неизвестных уравнений системы узловых потенциалов равно числу независимых узлов - n = q - 1 = 3 (p = 6 – число ветвей с неизвестными токами, q = 4- число узлов) Обозначим токи в резисторах, э.д.с. и токи источников тока в виде матриц столбцов (35), а потенциалы: 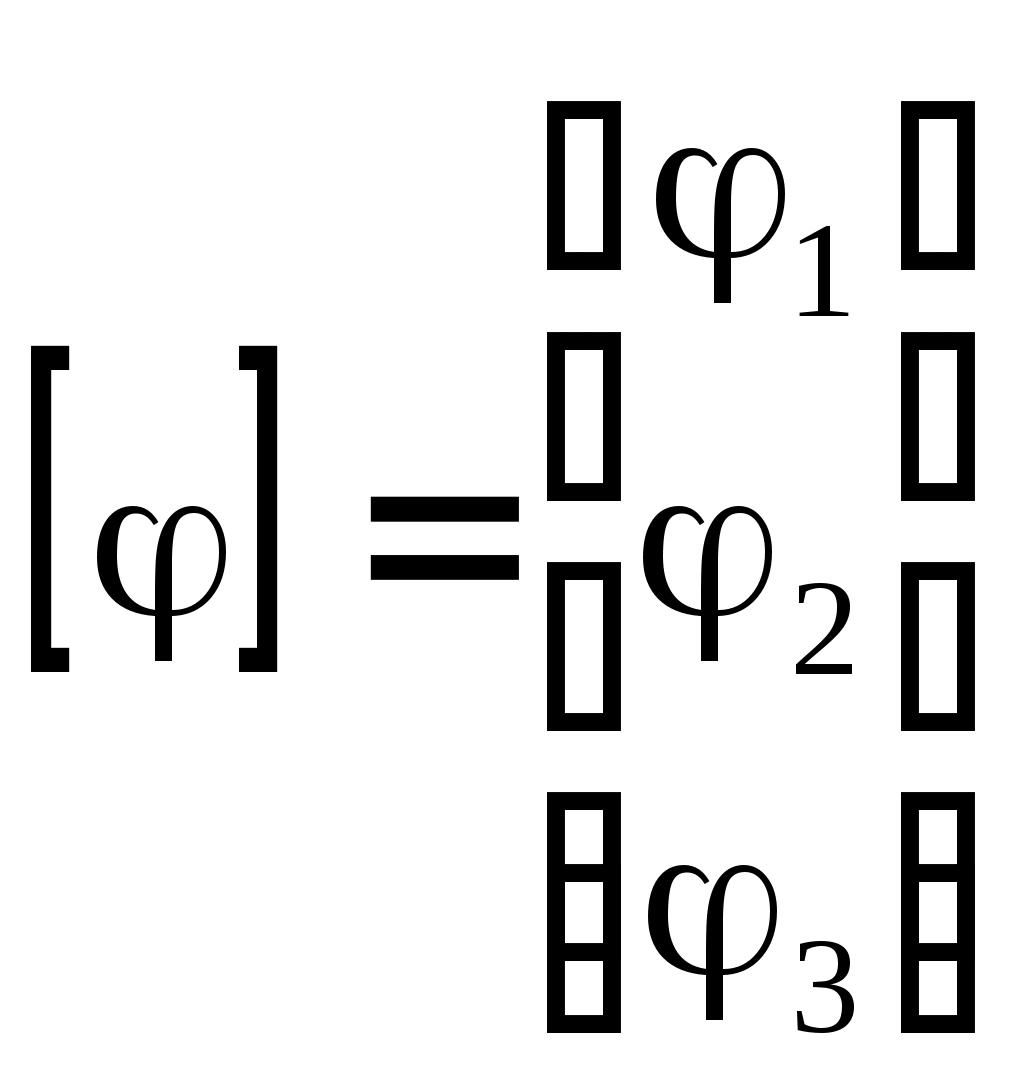 . (56) . (56)Проводимости ветвей 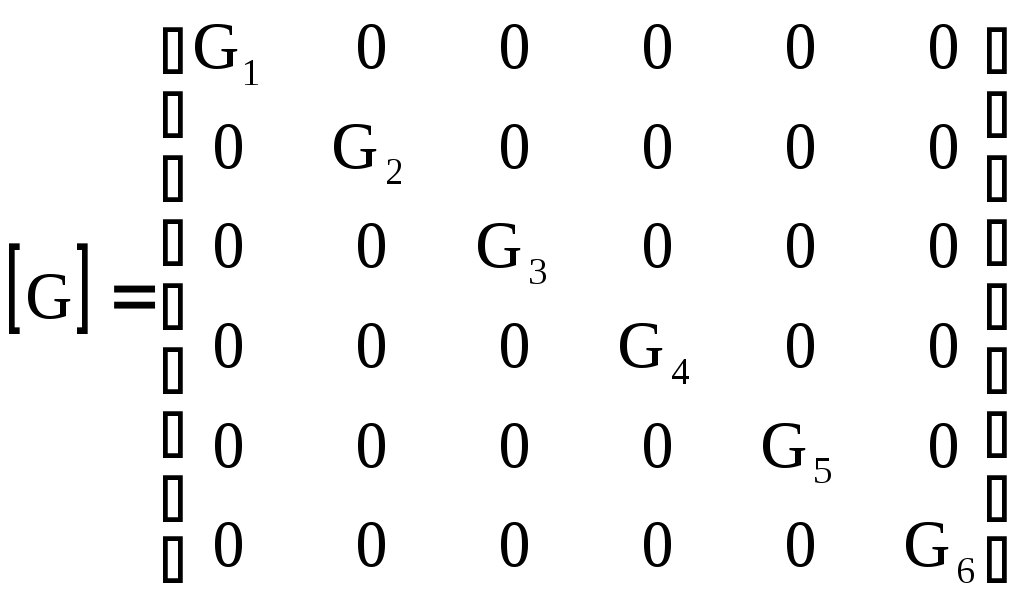 . (57) . (57)Определенная узловая матрица [A], составленная для графа, изображенного на рис. 16, 19, при условии, что узел 4 принят за базисный, имеет вид (37): Матрица узловых проводимостей(52): 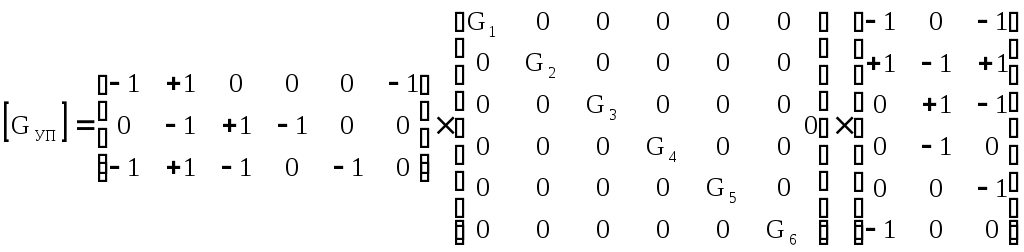 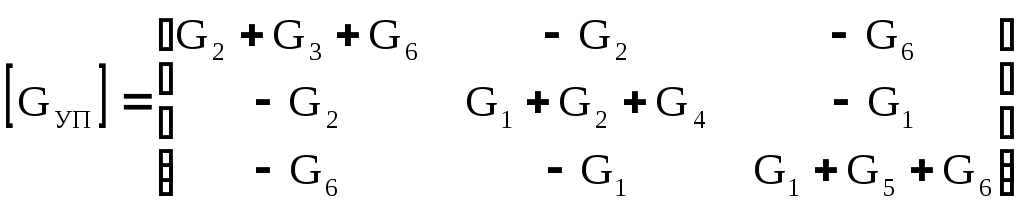 . (58) . (58)Матрица узловых токов (53) 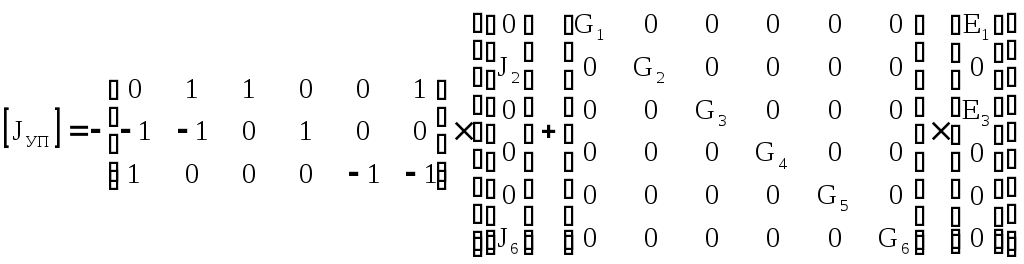 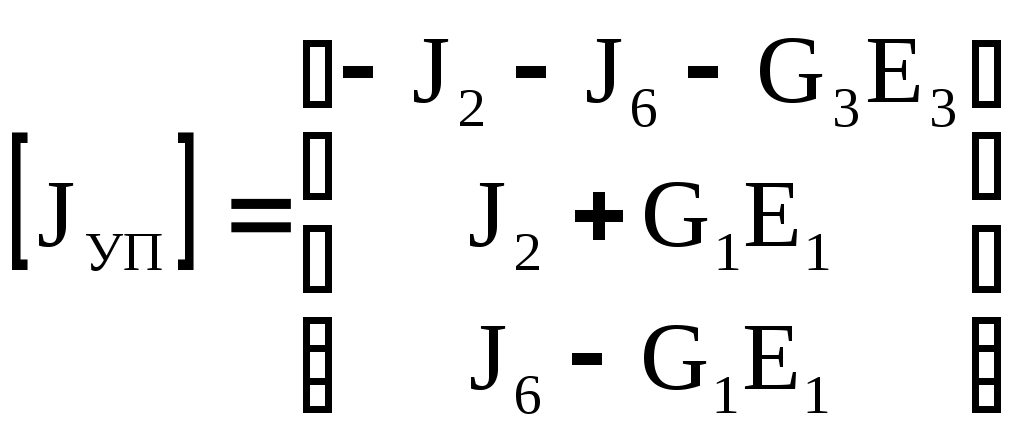 . (59) . (59)Итоговая система уравнений узловых потенциалов в матричной форме: 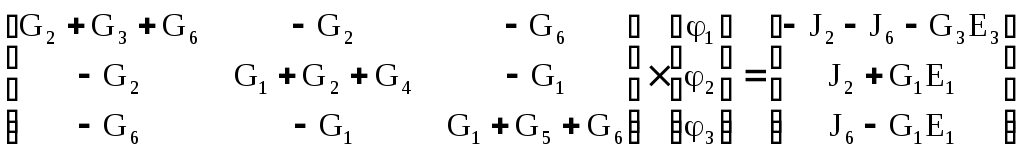 . (60) . (60)По (55) определим токи в резисторах: 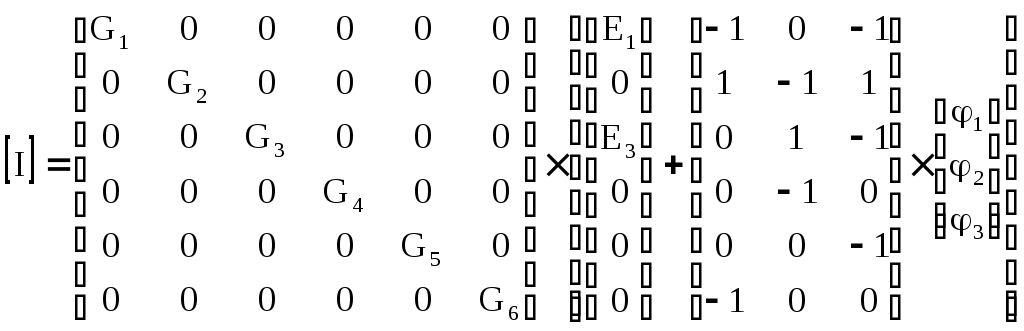 . (61) . (61)4.10.3. Формирование уравнений контурных токов в матричной форме Топологические матрицы [А], [В] и [Q] можно использовать для определения напряжений и токов ветвей по известным контурным токам. Использование контурных токов позволяет сократить порядок системы уравнений цепи в сравнении с уравнениями Кирхгофа на число независимых узлов. Контурные токи [IKT] определяют, как токи в независимых контурах, направления которых совпадают с направлениями обхода контуров. Токи в ветвях определяются как алгебраическая сумма контурных токов обтекающих данную ветвь. Столбцы контурной матрицы [В] содержат информацию о i- ой ветви, которая входит в контуры, и их взаимных направлениях. Представим контурные токи в виде матрицы столбца: 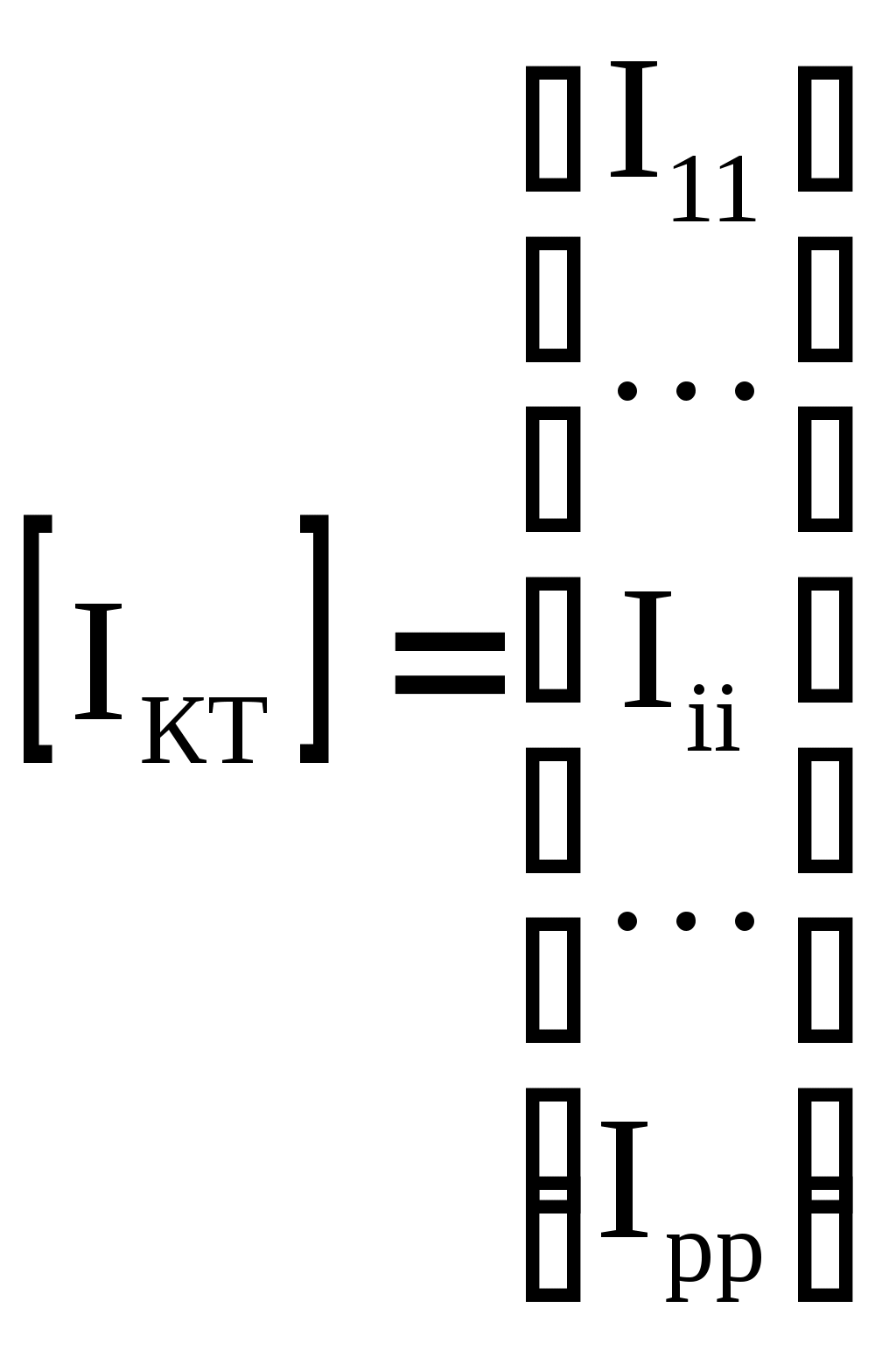 (62) (62)Токи в ветвях получим, умножив транспонированную контурную матрицу [Вт] (т. е. матрицу [В], в которой строки заменены столбцами) на матрицу контурных токов [IKT]: [IB] = [Вт] [IKT] (63) Для обобщённой ветви (рис. 20) токи в резисторах: [I] = [IB] − [J] = [Вт] [IKT] − [J] (64) Для получения уравнений контурных токов используем второй закон Кирхгофа в матричной форме: [B] [R] [I] = [B] [E] (65) Подставив в (65) (64) и (63) получим: [B] [R] [Вт] [IKT] = [B] [E] + [B] [R] [J] (66) Введём обозначение матриц: матрица сопротивлений второго закона Кирхгофа [RЗК] = [B] [R] (67 матрица контурных сопротивлений [RKT] = [RЗК] [Вт] (68) матрица контурных э. д. с [EKT] = [B] [[E] + [R] [J]]. (69) Запишем уравнений контурных токов в матричной форме: [RKT] [IKT] = [EKT]. (70) Рассмотрим пример рис. 15 формирования уравнений контурных токов в матричной форме. Пусть определению подлежат токи всех ветвей после расчёта контурных токов. Число неизвестных уравнений системы контурных токов равно числу независимых контуров– m = p − q +1 = 3 (p = 6 – число ветвей с неизвестными токами, q = 4- число узлов). Пусть токи ветвей 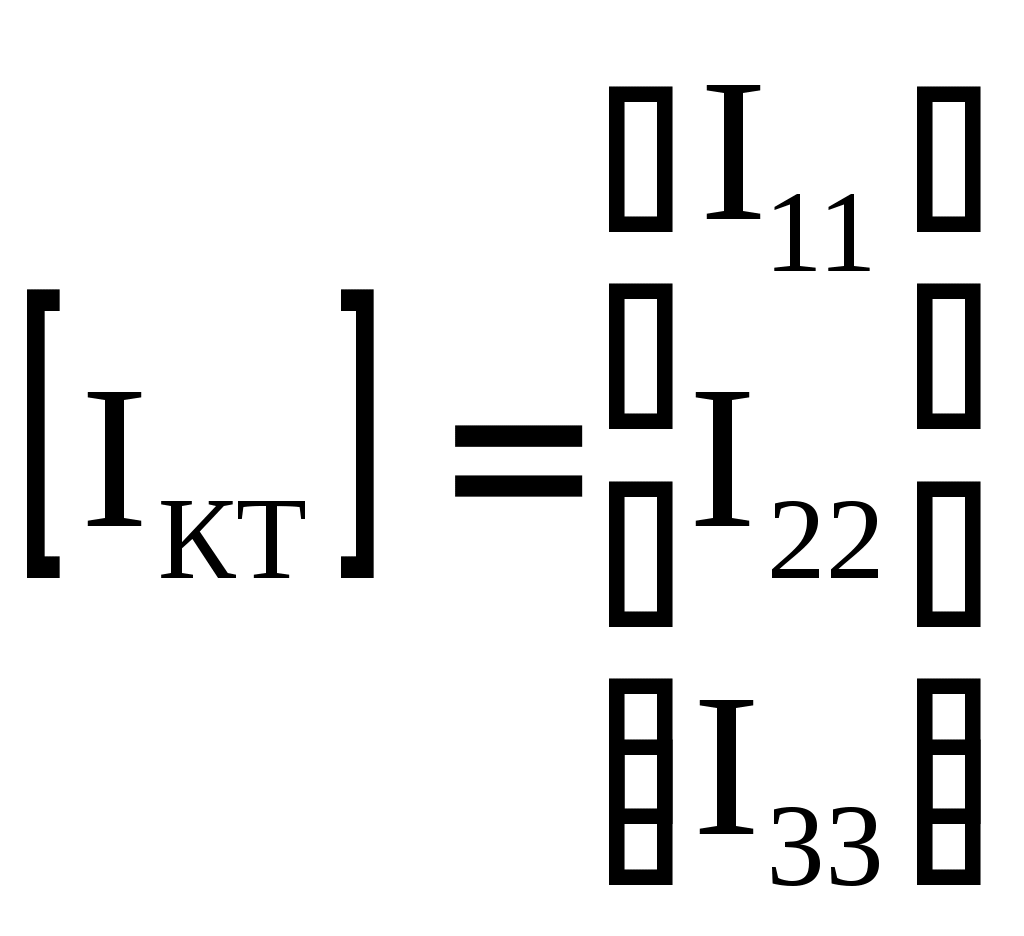 . (71) . (71)Сопротивления ветвей По (67), (68) и (69) определим матрицы сопротивлений второго закона Кирхгофа, контурных сопротивлений и контурных э. д. с. 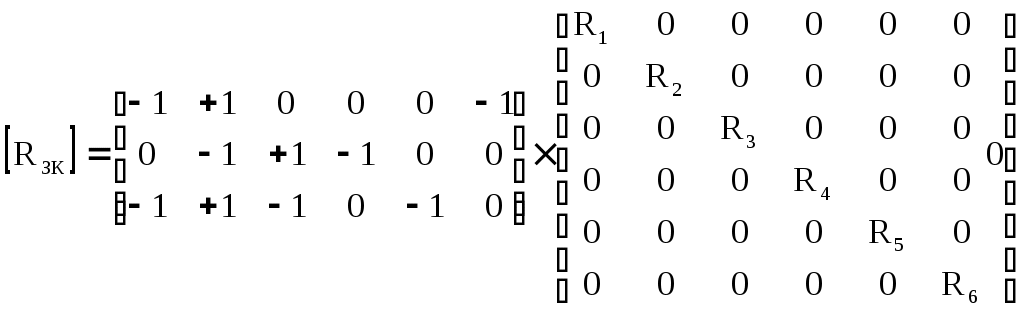 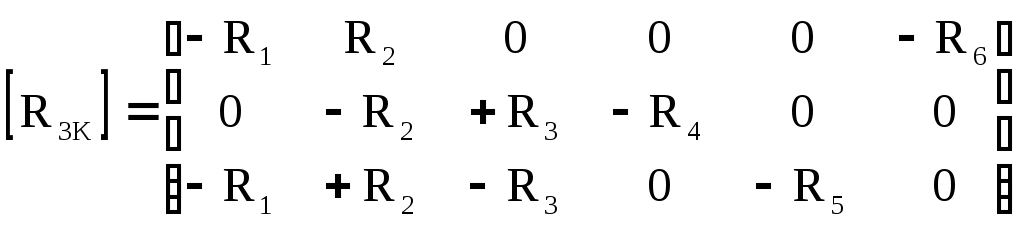 . (72) . (72)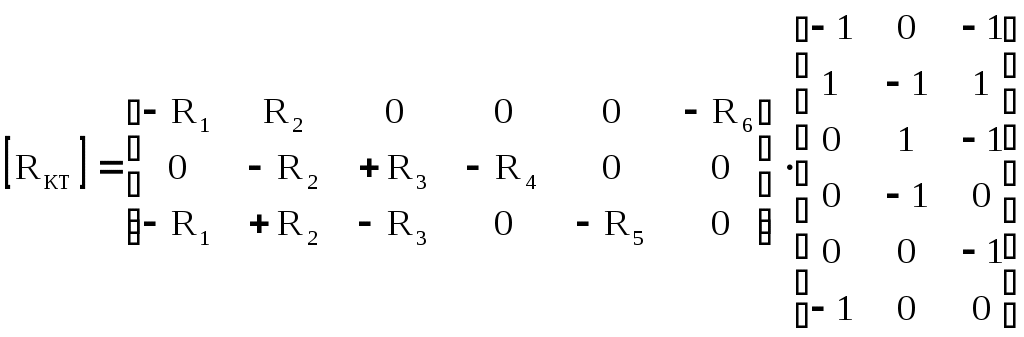 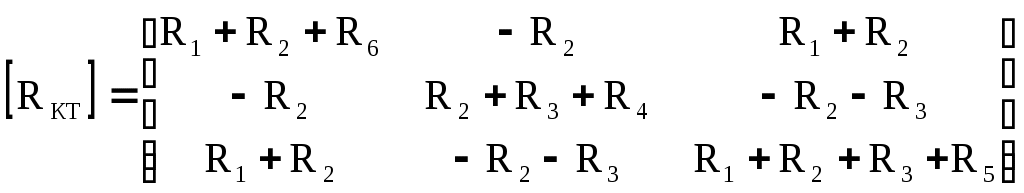 . (73) . (73)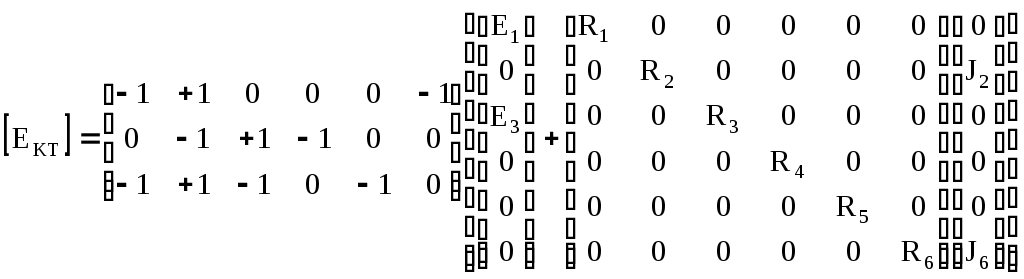 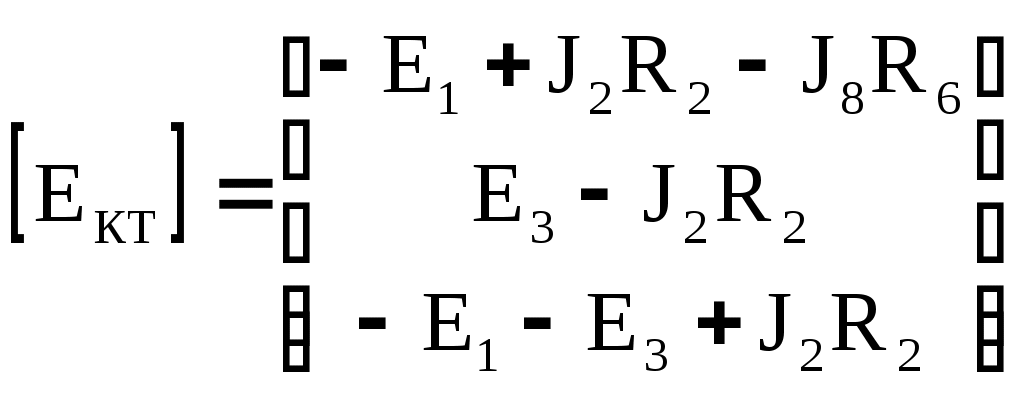 . (74) . (74) . (75) . (75)Для обобщённой ветви (рис. 1) токи в резисторах определим по (3): 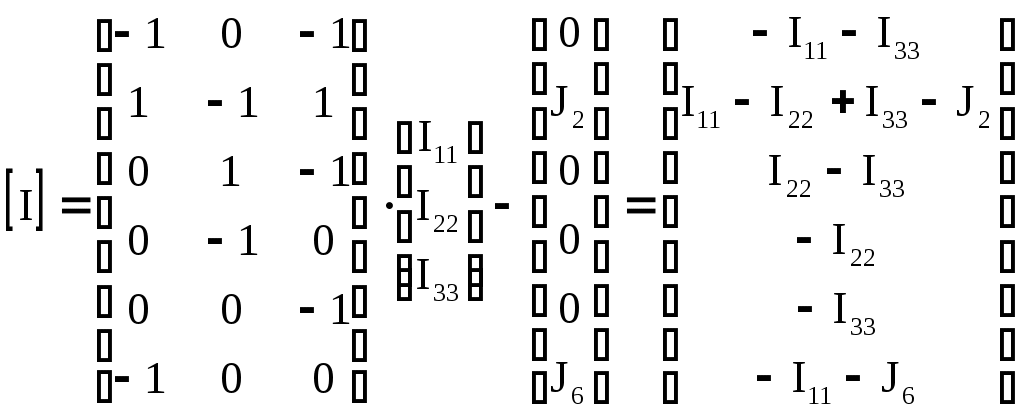 . (76) . (76)СПИСОК ЛИТЕРАТУРЫЗевеке Г.В., Ионкин П.А., Нетушил А.В. и др. Основы теории цепей. - М.: Энергия, 1989. - 528 с.: ил. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники, т.1. - М.: Энергия, 1981. - 536 с.: ил. Прянишников В.А. Теоретические основы электротехники. Курс лекций - СПб.: КОРОНА принт. 2000. - 368 с.: ил. Атабеков Г.И. Линейные электрические цепи. - М.: Энергия, 1978.-. 432 с.: ил. Бессонов Л.А. Теоретические основы электротехники. - М.: Высш. шк., 1984. - 559 с.: ил. Матханов П.А. Основы анализа электрических цепей. - М.: Высш. шк., 1990. - 400 с.: ил. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике. - М.: ГИФМЛ, 1962. - 680 с.: ил. Корн Г., Корн Т. Справочник по математике. - М.: Наука, 1977. – 720 с. : ил. 8. Разевиг В.Д. Моделирование аналоговых электронных устройств на персональных ЭВМ. - М.: Изд-во МЭИ, 1993.- 152 с.: ил. 9. Разевиг В.Д. Система схемотехнического моделирования MICRO-CAPV. - М.: Изд-во «СОЛОН», 1997. - 280 с.: ил. 10. Теоретические основы электротехники, т.1. Основы теории линейных цепей./ Под ред. П.А. Нонкина. - М.: Высшая школа, 1979. - 544 с.: ил. 11. Попов В.П. Основы теории цепей. - М.: Высш. шк., 1998 - 575 с.: ил. 12. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 544 с.: ил. 13. Добротворский И.Н. Лабораторный практикум по основам теории цепей. - М.: Высш. шк., 1986 - 192 с.: ил. |

 етви
етви етви
етви