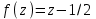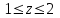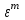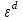ЛР5 Моделирование. новосибирский государственный технический университет
 Скачать 215.85 Kb. Скачать 215.85 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» _________________________________________________________________ Факультет автоматики и вычислительной техники Кафедра автоматики  ОТЧЁТ по лабораторной работе №5 « Имитационное моделирование случайных величин, обработка результатов моделирования» по дисциплине: «Моделирование» Выполнили:Проверила: студенты гр. АВТ-918 Пинигина Д.Л. Королев Даниил Плотников Михаил Новосибирск 2021 1. Цели лабораторной работы: - изучить алгоритмы и методы имитации случайных величин (СВ) и обработки результатов моделирования; - ознакомиться и получить практические навыки работы со средствами систем моделирования GPSS World, ExtendSim, реализующими имитационное моделирование СВ и обработку результатов моделирования; - сравнить эффективность использования (простота реализации, объем вычислений, точность) различных методов и программных средств для имитационного моделирования СВ. 2. Задание к лабораторной работе 1. Осуществить моделирование последовательности значений случайной величины (СВ) Z с заданной функцией плотности распределения вероятностей в соответствии с вариантом (см. табл. 1). Длина последовательности N=200. Таблица 1.
1.1. Реализовать моделирование на основе использования метода обратной функции в разных программных средах (ExtendSim, GPSS World, Statistica, Excel, C++ …). Получить две выборки, используя разные программные средства (на выбор). 1.2. Реализовать моделирование на основе использования метода Неймана с использованием любых программных средств. 1.3. Фрагменты сгенерированных последовательностей (первые 10 значений) оформить в виде табл. 2. Моделирование Задана функция плотности распределения вероятности СВ Y: 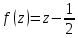 (1) (1)СВ Z изменяется в диапазоне от 1 до 2. Согласно методу обратной функции найдем выражение для функции распределения вероятностей СВ Z и приравняем к СЧ, распределенному равномерно на [1,2]: 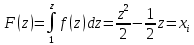 (2) Из (2) найдем выражение для 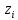 : :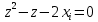 D= 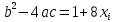 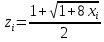 (3) (3)Выбран положительный корень, учитывая диапазон изменения СВ Z. Реализуем моделирование на основе обратной функции в программных средах: ExtendSim, GPSS, Excel. Метод Неймана реализуем в C++. ExtendSim:  Рис 1. Модель в ExtendSim 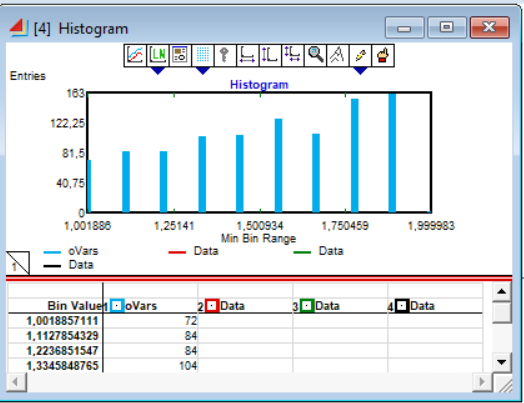 Рис 2. Гистограмма в ExtendSim Математическое ожидание M=1,57; Дисперсия D=0,08 GPSS: Ниже приведена программа, моделирующая значения CВY и вывод статистических характеристик в GPSS 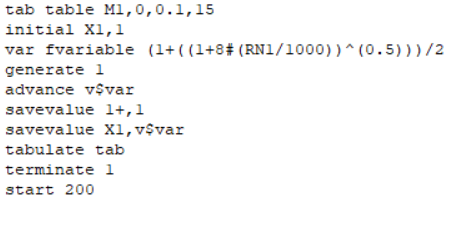 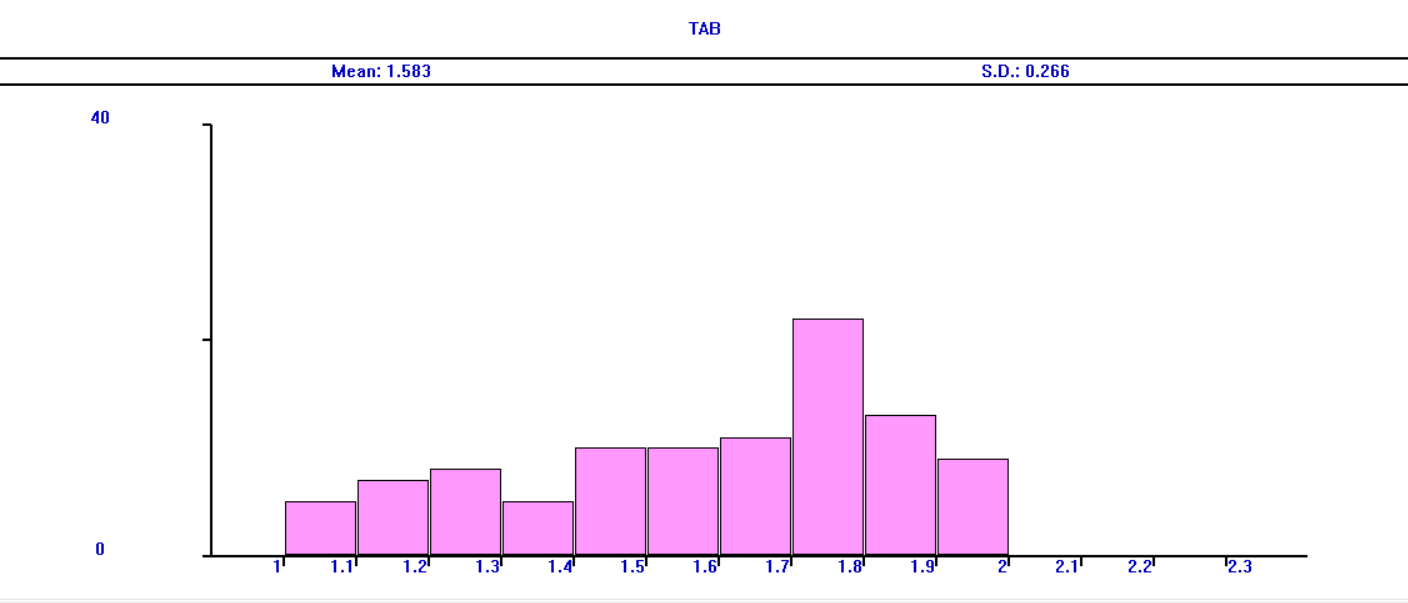 Рис 3. Гистограмма времени пребывания заявки в системе Мат ожидание M=1,582 Дисперсия D=0,07 C++: Реализация метода Неймана на языке c++ 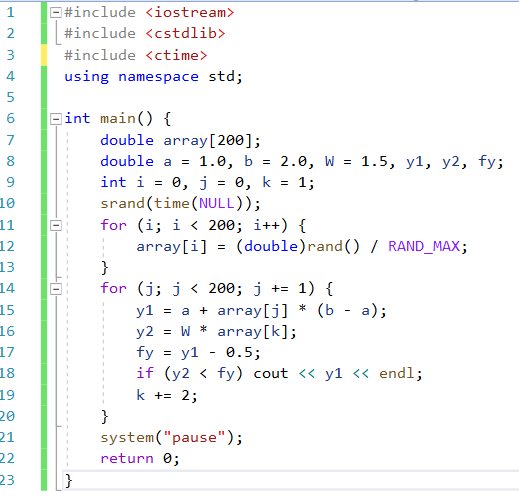 Мат ожидание M=1,5101 Дисперсия D=0,8319 Excel: 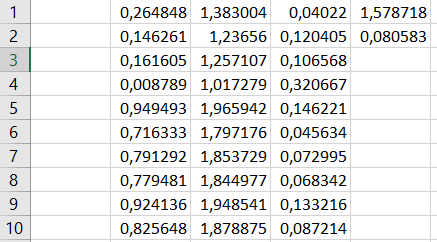 Мат ожидание M=1,5787 Дисперсия D=0,0806 Таблица 2.
Таблица 3. Вычисленные значения M(X) и D(X) для разных методов моделирования
Часть 2. Обработка результатов моделирования 2.1 Теоретический расчет значений математического ожидания и дисперсии заданной СВ Z. 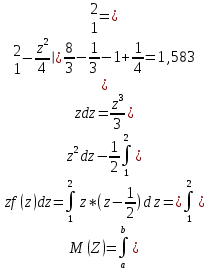 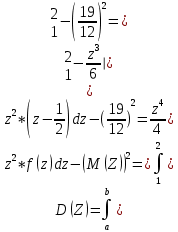 Вычислим ошибки оценивания математического ожидания и дисперсии (точность оценки) при использовании разных методов моделирования и программных средств. Результаты представим в табл. 4. Таблица 4.
Моделирования в различных средах показали отличную точность. Ошибки оценивания математического ожидания и дисперсии (точность оценки) различаются, не превышая погрешности в 3%. Для смоделированных значений СВ Z реализуем проверку гипотезы о согласии эмпирического и теоретического распределений на основе критерия согласия хи-квадрат (Пирсона). С помощью выборки из 200 значений по правилу Стёрджеса определим оптимальное количество интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины: 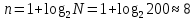 где N{\displaystyle N}N — общее число наблюдений величины Определим длину каждого интервала l= 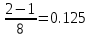 Построим интервальный вариационный ряд
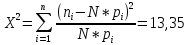 Положим α = 0,05, число степеней свободы r = n – 1 = 7. Тогда по таблице квантилей распределения хи-квадрат 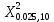 =1,6899, =1,6899, 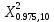 =16,0128. =16,0128. Значение 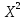 попадает в этот интервал. Гипотеза принята при данном попадает в этот интервал. Гипотеза принята при данномзначении α. Построим 95% доверительные интервалы для M(Z)и D(Z) по выборке из 200 значений, сформированной в Excel: M(Z)=1,549413 D(Z)=0,085423 σ=0,29227 t0,95=1,96 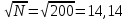 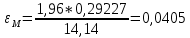 M(Z) 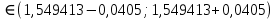 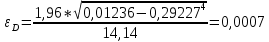 D(Z) 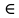 (0,085423-0,0007; 0,085423+0,0007) (0,085423-0,0007; 0,085423+0,0007)Оценим объем выборки, необходимый для оценки математического ожидания и дисперсии: t0,95=1,96 t0,99=2,576 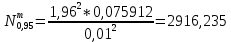 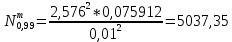 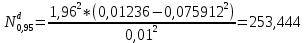 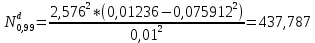 Таблица 5 Оценка объема выборки
Выводы Было проведено моделирование заданной функции в четырех программных средах на основе метода обратной функции и метода Неймана. Метод обратной функции включает в себя необходимость вычисления интегралов, что может быть трудоемким процессом для вычислительного устройства, поэтому целесообразнее пользоваться приближенными методами, например, метод Неймана. Его легко запрограммировать, зная заданные начальные параметры. При этом точности методов практически не отличаются. При проверке гипотезы о согласии эмпирического и теоретического распределений на основе критерия согласия хи-квадрат (Пирсона) получили, что данная гипотеза подтверждается, так как значение хи-квадрат попадает в заданный диапазон для 8 интервалов. Значения объёмов выборки для достоверностей 95% и 99% как для дисперсии, так и для мат. ожидания, отличаются. |