экономический баланс. вмф. Нтенсивности связей определяются с учетом следующих критериев
 Скачать 2.05 Mb.
|
|
нтенсивности связей определяются с учетом следующих критериев: Региональная близость страны j Членство стран i и j в международных политико-экономических объединениях вне МВФ. Каждому из указанных критериев приписывается определенный весовой коэффициент важности, общее значение интенсивности pij определяется аддитивным обобщенным критерием. При проведении анализа1, использовались следующие значения весов: - для региональной близости: Pr=0.35 - для политико-экономических объединений: Pb=0.65 Для определения степени региональной близости между странами используется следующий вариант: - Странам, имеющим общие границы с i, присваивается значение 1, странам, принадлежащим одной с i части света, - значение 0.6, странам, принадлежащим разным c i частям света – значение 0.4. Влияние членства стран i и j в других политико-экономических объединениях оценивается так: На первом этапе оценивается принадлежность пары стран множеству экономико-политических блоков. - Странам, состоящим вместе только в одном блоке, присваивается значение 0.5; - в двух блоках - 0.8; - в трех и более блоках - 1; - не входящим вместе ни в какой из рассматриваемых блоков – 0; На втором этапе для стран, состоящих вместе хотя бы в одном блоке, учитывается экономический характер блоков и степень их интеграции. Для этого значение apprxPij, полученное на первом этапе, складывается с максимальным значением экономической интеграции E(B) на множестве всех блоков B, куда вместе входят страны i и j, после чего полученная сумма делится на 2. Общая формула для данного частного критерия, таким образом, имеет вид: (3.1) 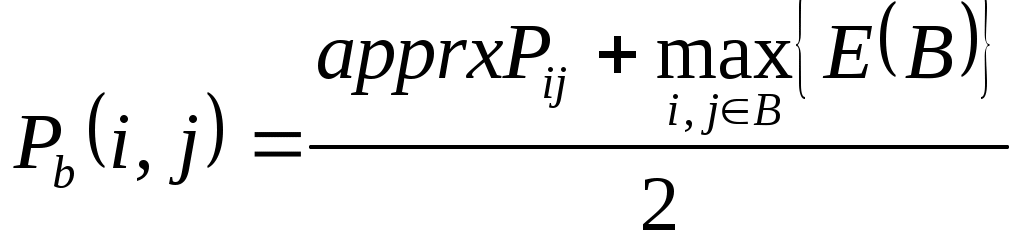 Значения E(B) являются действительными числами из интервала [0..1] и зависят от рассматриваемых блоков. В разделе 5 представлен один из возможных вариантов задания E(B) (см. таблицу 5.1). 4 Детальное описание модели4.1 Представление стран Каждой из 185 стран-участниц МВФ поставим в соответствие набор  , гдеv – число голосов данной страны. В силу взаимно однозначного соответствия по данному числу всегда можно получить значение квоты, и наоборот.  – профиль предпочтений данной страны iотносительно вступления в объединение с любой из остальных стран, основанный на критериях из раздела 3. Компонентами  являются числа pij, (такие, что 0≤pij≤1, ; N=185 - число стран)называемые интенсивностями связей страны iсо страной j, которые затем используются для расчета индекса влияния в рамках объединения. Мы будем интерпретировать pij как вероятность того, что страна i вступит в коалицию со страной j. – индекс влияния страны в масштабе Исполнительного совета – индекс влияния страны в масштабе объединения4.2 Представление объединений Каждому из 24 объединений2 из Исполнительного Совета, поставим в соответствие набор стран-участников данного объединения  4.3 Индексы влияния с учетом предпочтений участников Пусть имеется объединение V из l стран, принимающих решения голосованием с порогом q. Полагаем, что никакая страна не может воздерживаться от голосования. Назовем коалицию  выигрывающей, если она может определить общее решение в V без учета голосов остальных стран, т.е. сумма голосов стран, в нее входящих, не меньше q. Страна в выигрывающей коалиции называется ключевой, если при её выходе коалиция перестаёт быть выигрывающей. Будем говорить, что страна i изменяет исход голосования (совершает перемену (swing)), если коалиция ω проигрывающая, а коалиция ω+{i} - выигрывающая. Следуя 4, для оценки влияния каждой страны в масштабе Исполнительного совета будем использовать следующий подход: - Рассмотрим систему непрямых выборов. - Влияние каждой страны определяется ее влиянием в масштабе объединения и влиянием объединения в масштабе Исполнительного совета. - Индекс влияния представляет собой арифметическое произведение индекса влияния страны в объединении (т.е. )и индекса влияния объединения в Исполнительном совете.На уровне объединения мы используем некоторую модификацию индекса влияния Пенроуза, которая позволяет учитывать предпочтения участников объединения относительно вступления в коалицию. Мы будем следовать подходу из 1. Считая предпочтения каждой страны заданными в профиле предпочтений , в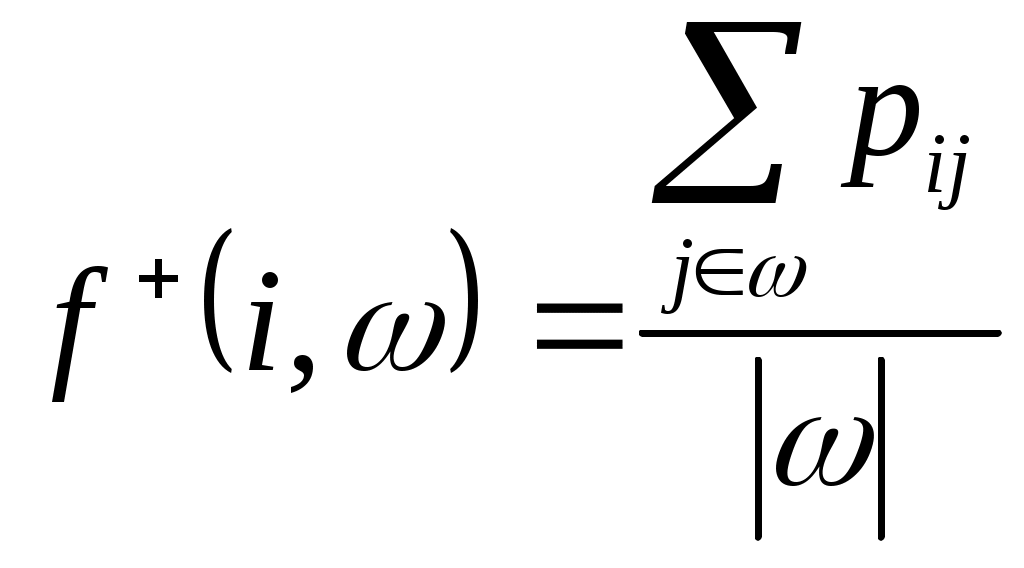ведем усредненную интенсивность связей страны i с другими членами коалиции ω так:(1)  Здесь и далее pij - компоненты .По аналогии введем усредненную интенсивность связей других стран коалиции со страной i: (2) 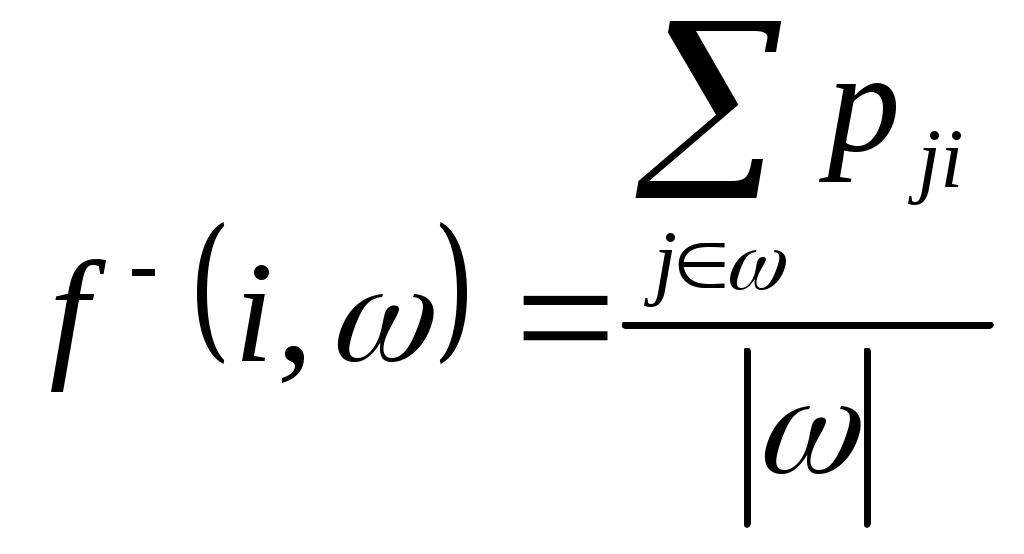 Нам также потребуется средняя интенсивность связей внутри коалиции, определяемая следующим образом: (3) 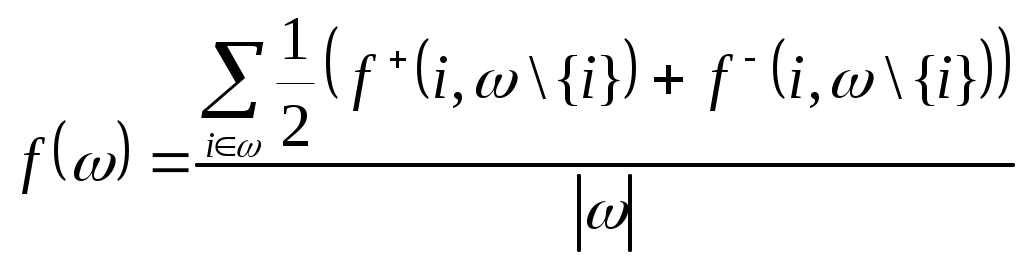 Индекс влияния с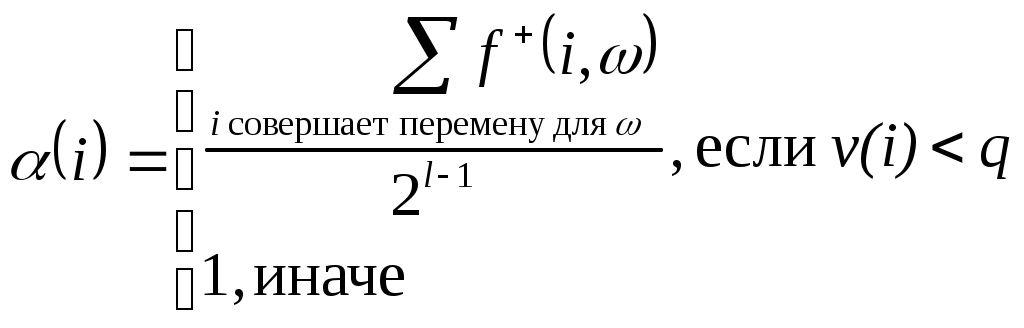траныi в масштабе объединенияопределим так:(4)  где l – число стран в объединении, v(i) – число голосов участника i, q – порог принятия решений при голосовании. Отметим, что если предпочтения всех участников по вступлению в коалицию друг с другом максимальны и равны 1, индекс в формуле (4) представляет собой индекс Пенроуза3.Переходя к рассмотрению влияния уровеня Исполнительного совета, найдем формально вероятность того, что объединение V проголосует «за»: (5) 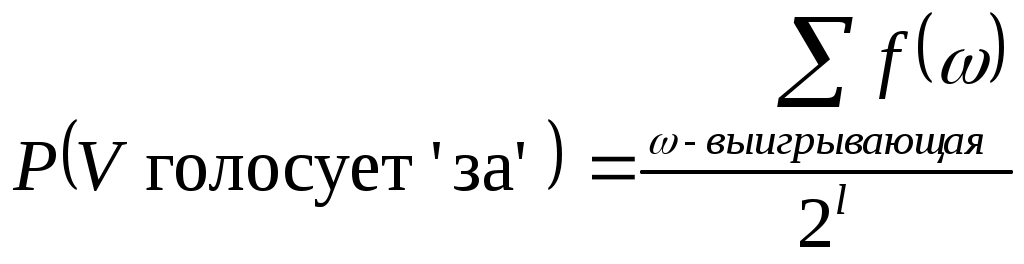 Иными словами, предположим, что каждая выигрывающая коалиция имеет степень внутренней согласованности, определяемую функцией f(ω), и чем больше эта величина, тем более вероятным является образование такой коалиции4. Определим индекс влияния объединения в масштабе Исполнительного совета как вероятность такого события, что объединение Vявляется решающим5. Для этого: Из множества всех возможных разбиений Исполнительного совета на коалиции голосующих «за» и «против», выберем те, в которых V может совершить перемену для одной из коалиций. Каждое такое разбиение представляет собой набор 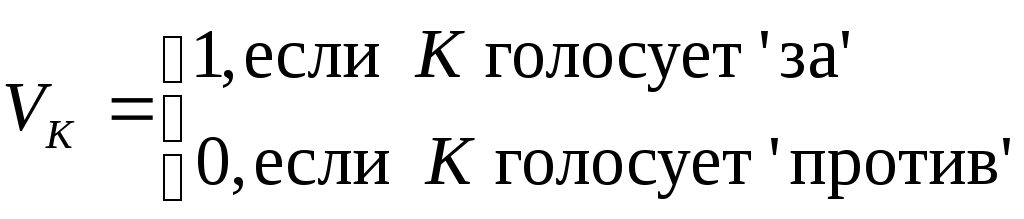 , где компонента VK обозначает позицию соответвующего объединения в данном разбиении,  , M=24 – число объединенийНайдем вероятность возникновения каждого из разбиений, выбранных в п.1) как произведение вероятностей событий, заключающихся в том, что каждое объединение K, K≠V, проголосует «за» (соответственно, «против»), если такой должна быть его позиция в соответствии с выбранным разбиением6. Сложив все вероятности, найденные в предыдущем пункте, получим вероятность7 того, что объединение V является решающим8. Таким образом, индекс влияния на уровне Исполнительного совета для каждого объединения V определяется как: (6) 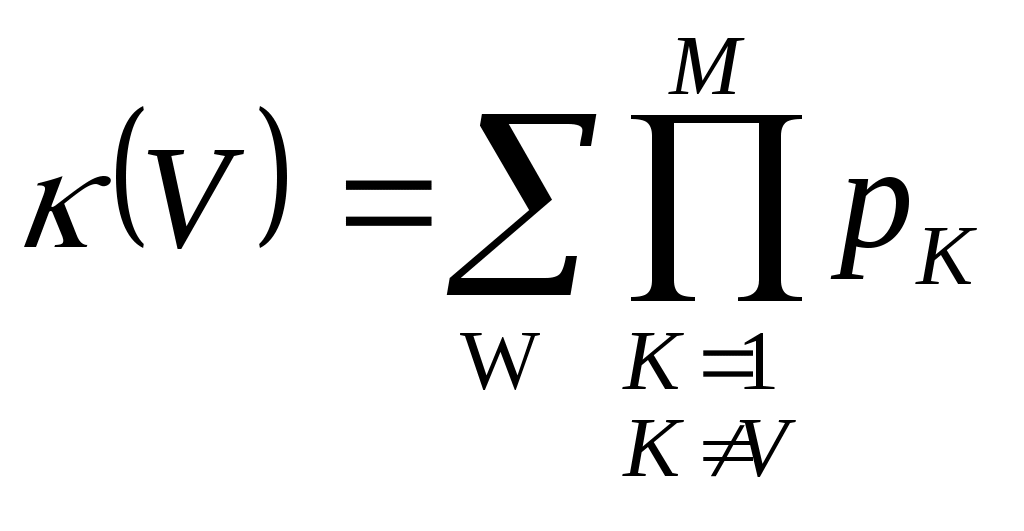 где суммирование ведется по всем разбиениям W выбираемым на шаге 1), а 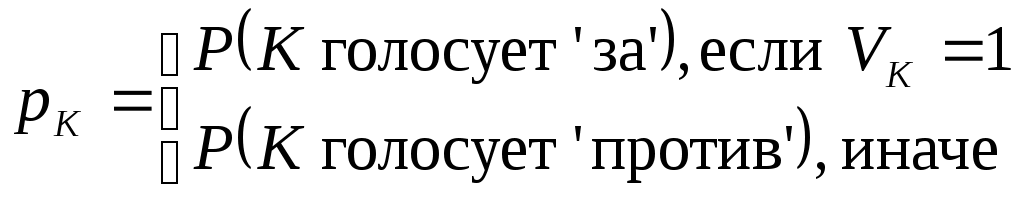 . Вероятности  определяются по формуле (5), причем  .Теперь определим для каждой страны iиз объединения V общий индекс влияния: (7)  5 Анализ распределения актуального влияния в ФондеМы провели анализ влияния в Исполнительном совете по состоянию на март 2007. Для каждой страны было получено 3 индекса, отражающие ее влияние в Совете для рассматриваемых случаев большинства. 5.1 Определение предпочтений стран с учетом выбранных критериев Предпочтения относительно регионального расположения определялись согласно правилу, указанному в разделе 3 при помощи политической карты мира. Для определения предпочтений относительно международных политико-экономических блоков были выбраны основные блоки, действовавшие на момент проведения анализа, некоторые из которых приводятся в таблице 5.1. Итоговые предпочтения для каждой страны определялись путем свертки частных предпочтений на основе выбранных критериев с весовыми коэффициентами Pr=0.35 и Pb=0.65 для регионального и экономического критериев, соответственно. Таблица 5. 1
5.2 Основные результаты Значения рассчитанных индексов для всех стран-участниц приводятся в [2]. В таблице 5.2 для примера приводятся значения индексов для некоторых стран. Как и следовало ожидать, при увеличении порога принятия решений (от простого большинства до большинства в 85%), абсолютное влияние всех объединений уменьшается. Любопытно отметить, что максимальным абсолютным влиянием при простом большинстве и большинстве в 70% обладает США, однако при большинстве в 85% лидером оказывается Нидерландское объединение. Таблица 5. 2
Для более детального анализа для каждого объединения были вычислены индексы влияния Пенроуза и Банцафа, которые затем сравнивались с индексами κ и их нормализованными вариантами, соответственно. В результате для рассматриваемых вариантов большинства, индекс Пенроуза всегда превышал индекс κ, при этом нормализованные индексы показывали различную динамику. Для индексов влияния уровня объединения α отметим, что учет предпочтений почти всегда11 уменьшает величину этого индекса по сравнению с аналогичным индексом Пенроуза. Действительно, из формулы (4) следует, что для того, чтобы индекс α достиг величины индекса Пенроуза, необходимо иметь максимально возможные для всех стран предпочтения (равные 1), что практически не наблюдается. Из всех объединений можно выделить объединения, имеющие «диктатора»12, т.е. страну, с количеством голосов, превышающих 50% всех голосов объединения. Для «диктаторов» и индекс α, и индекс Пенроуза равны 1. Для всех остальных стран в таких объединениях индекс влияния α, как и индекс Пенроуза равен 0, в силу того, что они не могут совершить ни одной перемены. Кроме того, абсолютные индексы влияния могут быть равны 0 для некоторой страны и в случае, когда в объединении нет «диктатора», но количество голосов, которыми эта страна обладает, не позволяет ей совершить ни одной перемены. Примером может служить Шведское объединение, в котором индекс влияния Эстонии равен 0. В остальных случаях, значения индекса α отличны от нуля, но в зависимости от состава объединения могут быть весьма близки к нулю для некоторых стран. Полученные результаты, справедливы и при иных предположениях о предпочтениях участников, не слишком сильно отличающихся от модельного варианта в силу устойчивости индексов относительно выбранных весовых коэффициентов частных предпочтений. 6 Список литературыАлескеров Ф.Т. Индексы влияния, учитывающие предпочтения участников по созданию коалиций //Доклады Академии Наук, 2007, т.414, №5, с.594-597 Алескеров Ф.Т., Калягин В.А., Погорельский К.Б. Мультиагентная модель динамики влияния стран-участниц МВФ: Препринт WP7/2007/06.-М.: ГУ ВШЭ, 2007.-84 с. http://new.hse.ru/C3/C18/preprintsID/default.aspx?view=WP7/2007/06 Международный Валютный Фонд (МВФ) //Энциклопедия Кругосвет.- http://www.krugosvet.ru/articles/63/1006379/1006379a1.htm Felsenthal, D. Machover, M. Annexations and alliances: When are blocs advantageous a priori? //Social Choice and Welfare.- 2002.-vol. 19.-pp 295–312 Leech, D., Leech, R. Voting Power in the Bretton Woods Institutions /D.Leech, R.Leech.- University of Warwick, Centre for the Study of Globalisation and Regionalisation, Discussion Paper 154/04, 2004 Leech, D. Voting Power in the Governance of the International Monetary Fund //Annals of Operations Research.- 2002.- vol.109.- pp 375-397 Leech, D., Leech, R. Voting Power Implications of a Unified European Representation at the IMF //LSE eprint 00000565, London School of Economics.- 2005.- http://www.lse.ac.uk/collections/VPP/ Van Houtven, L. Governance of the IMF: decision making, institutional oversight, transparency and accountability //IMF Pamphlet Series no. 53.-IMF: Washington, 2002. Articles of Agreement of the International Monetary Fund. www.imf.org/external/pubs/ft/aa/index.htm 1 См. раздел 5. 2 Без потери общности можно считать, что 5 стран, назначающих Исполниельнных директоров , также являются объединениями, состоящими из одной страны. 3 Определения индексов Пенроуза и Банцафа приводятся, например, в 4. 4 Отметим, что формула (5) представляет собой модифицированный индекс «The Power of the Body to Act» (PTA), предложенный Колмэном (Coleman) с тем отличием, что в PTA для всех коалиций f(ω)=1. Подробнее см. в 6. 5 Т.е. голоса объединения определяют исход голосования. 6 Подчеркнем, что все объединения голосуют независимо друг от друга (мы отвергаем возможность объединений организовывать альянсы), а вероятности каждого объединения проголосовать «за» или «против» определяются с помощью (5). 7 Заметим, что события, состоящие в возникновении различных коалиций, являются несовместными и в сумме дают достоверное событие – один из возможных результатов голосования. 8 Также отметим, что вероятность, с которой само объединение V голосует «за» или «против», при расчете роли не играет, т.к. по определению Vбудет решающим независимо от того, как оно проголосует. 9 Полный список приводится в [2]. 10 См. раздел 3. 11 За исключением двух крайних случаев – страны с нулевым влиянием и страны-диктатора, см. ниже. 12 Это, в частности, Итальянское, Канадское, Швейцарское, Бразильское и Индийское объединения. |