ЛЕММА 3: Пусть 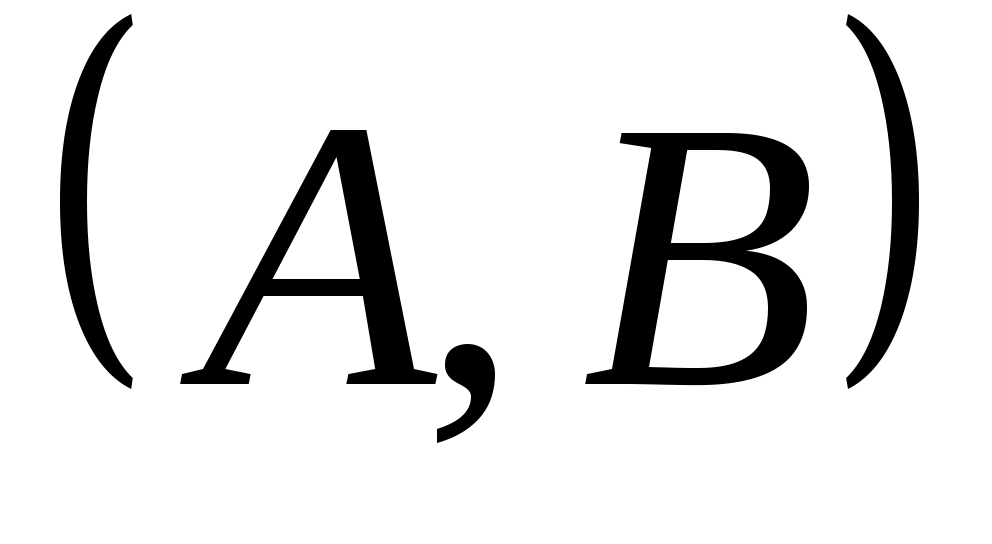 управляемо, а управляемо, а 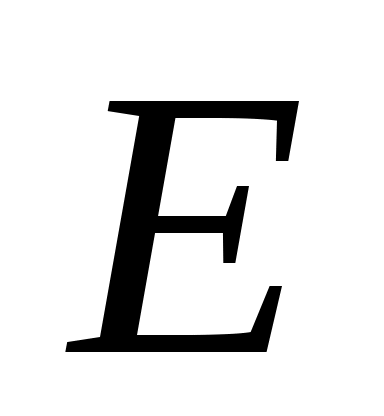 циклически. Существует такой вектор циклически. Существует такой вектор 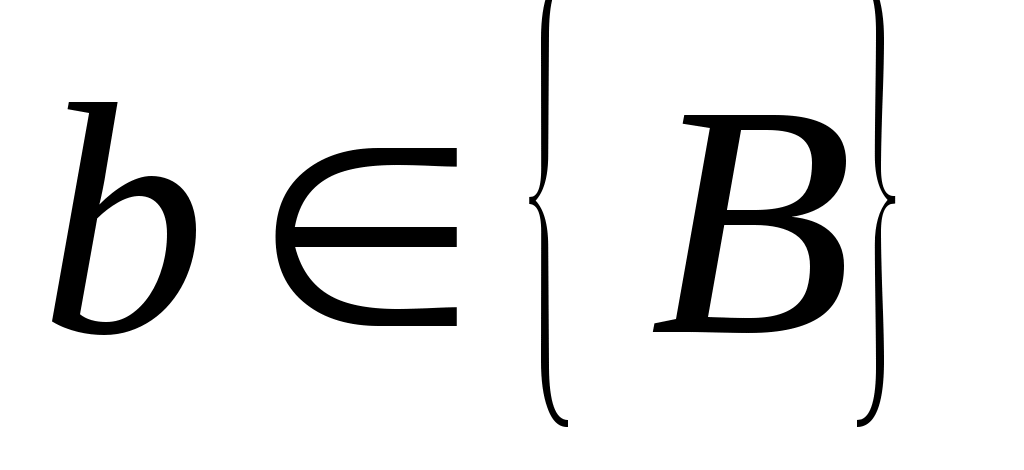 , что , что 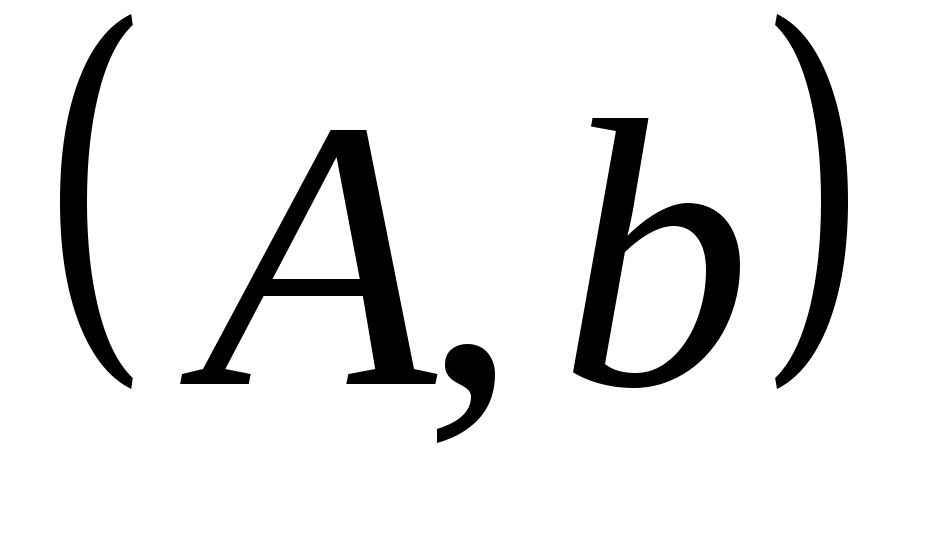 является управляемым. является управляемым.
Доказательство: для 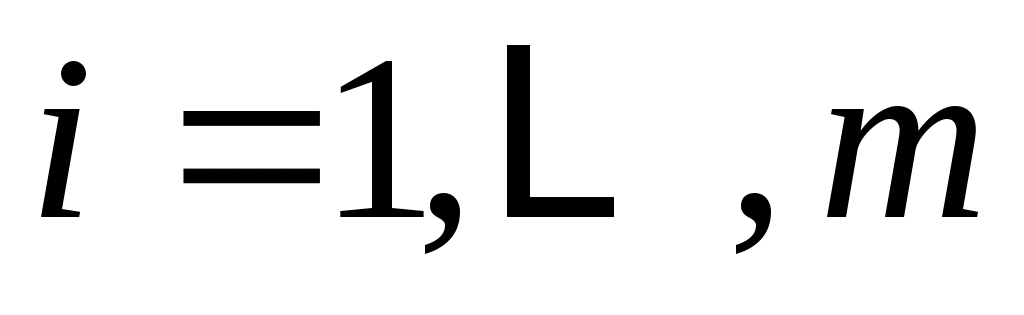 пусть пусть 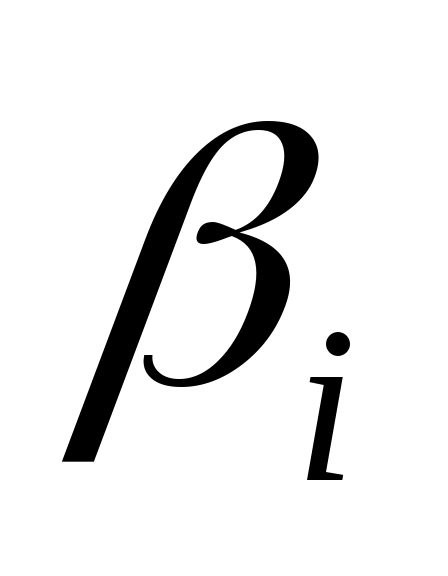 будет минимальный полином в будет минимальный полином в 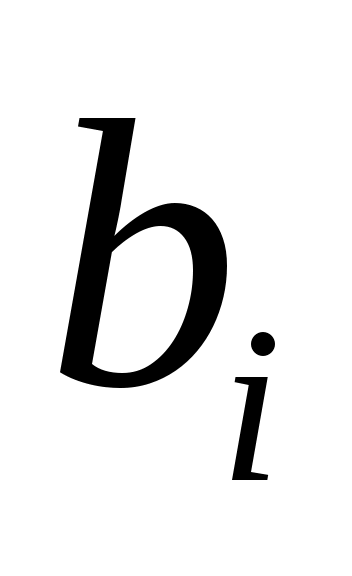 , а , а 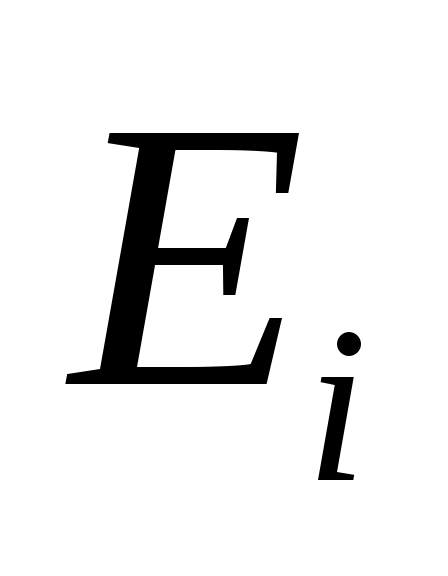 циклическое подпространство, порожденное циклическое подпространство, порожденное 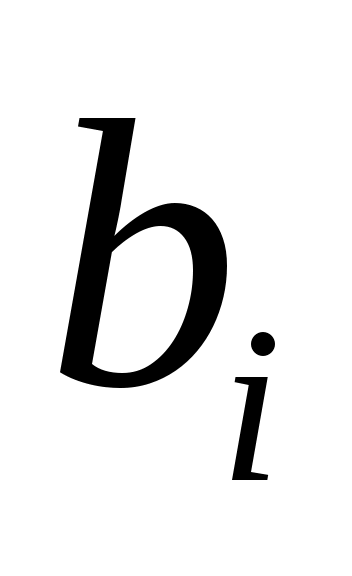 . Таким образом, . Таким образом, 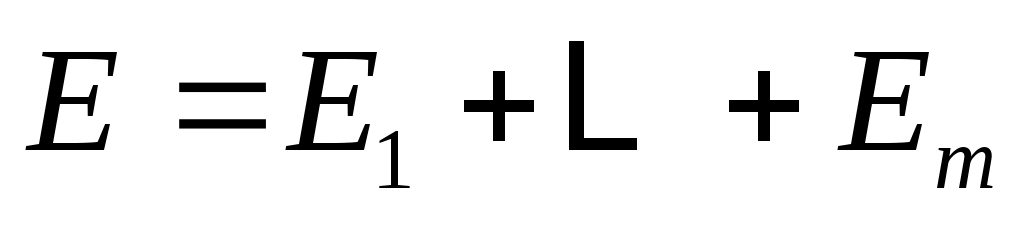 , и, если a является минимальный полином , и, если a является минимальный полином 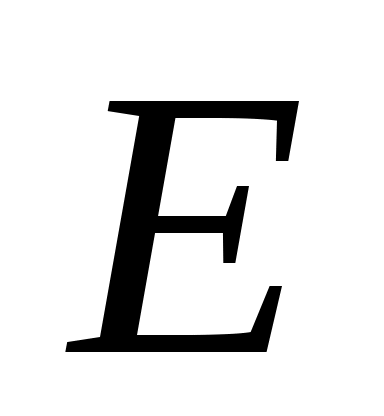 , ,
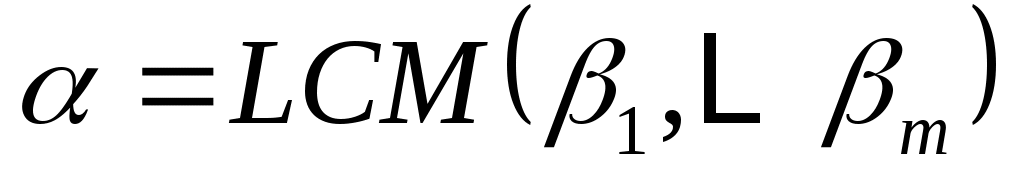 . .
Пусть 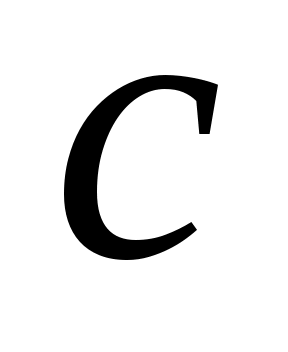 - будет генератором - будет генератором 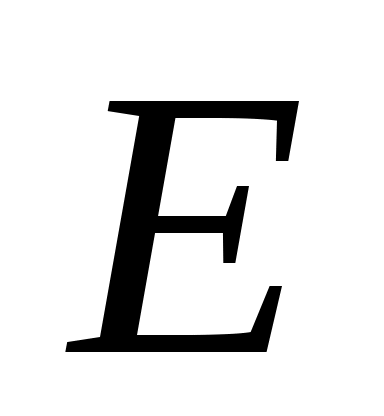 . Существуют многочлены . Существуют многочлены 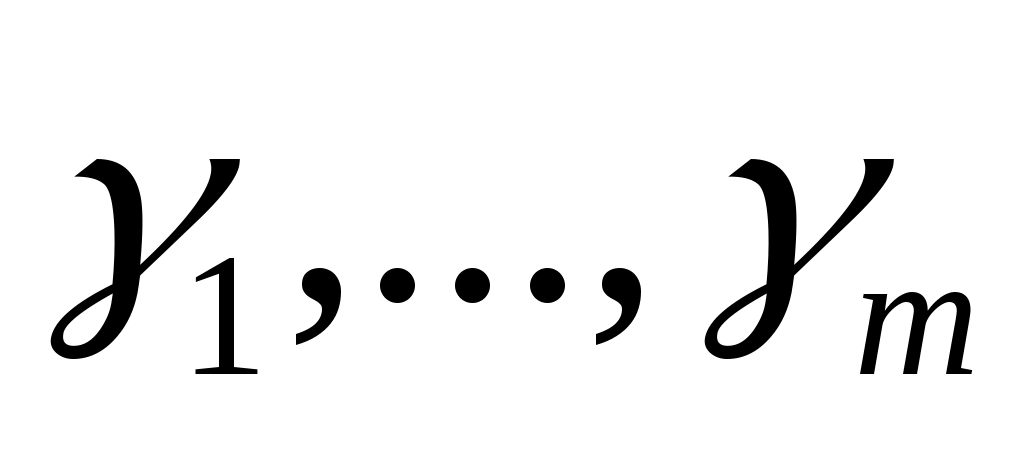 такое что такое что 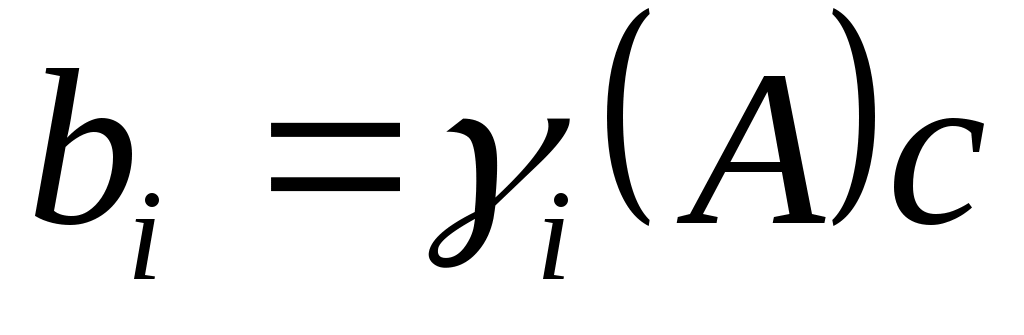 , ,  . Существование действительных чисел . Существование действительных чисел  , будет доказано, что , будет доказано, что  генерирует генерирует 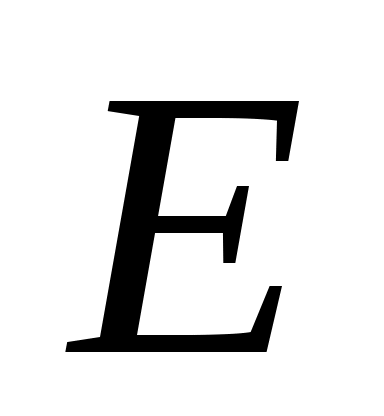 . По лемме 2 достаточно выбрать . По лемме 2 достаточно выбрать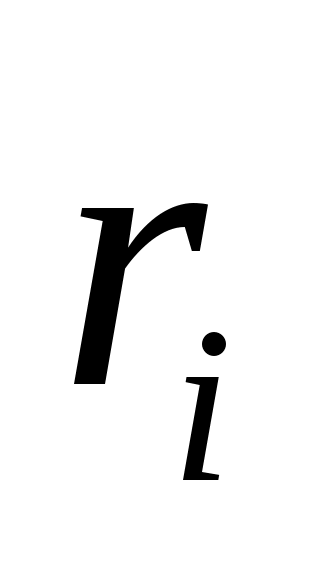 так, чтобы так, чтобы
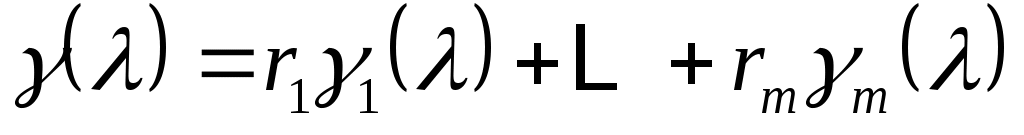
взаимно с  . .
Для этого сначала отметим, что
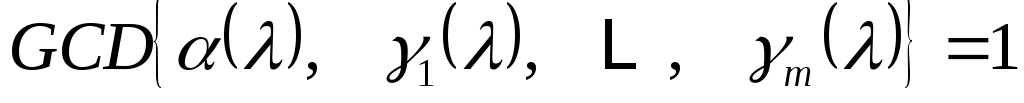 . (5) . (5)
На самом деле, если 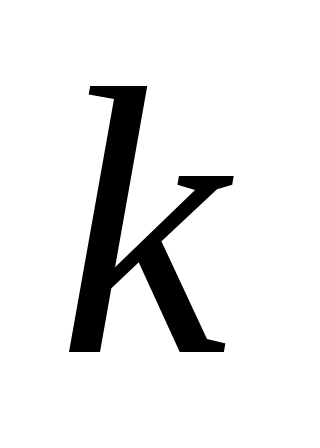 это наибольший общий делитель слева, то это наибольший общий делитель слева, то
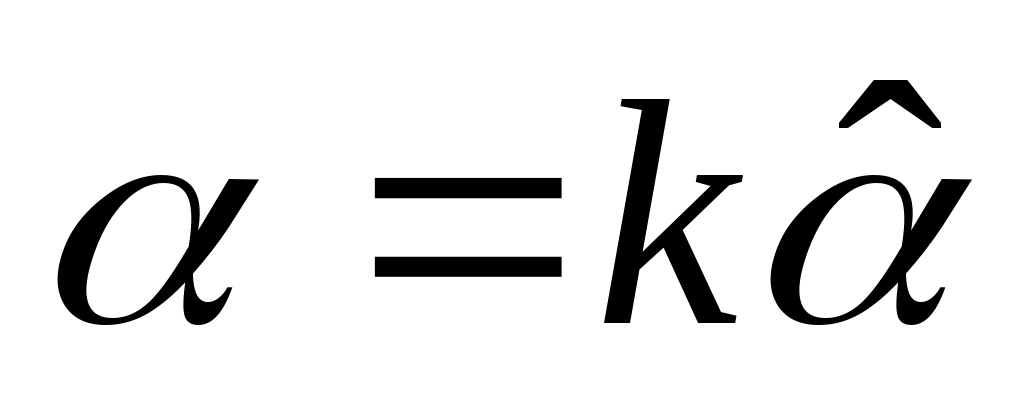
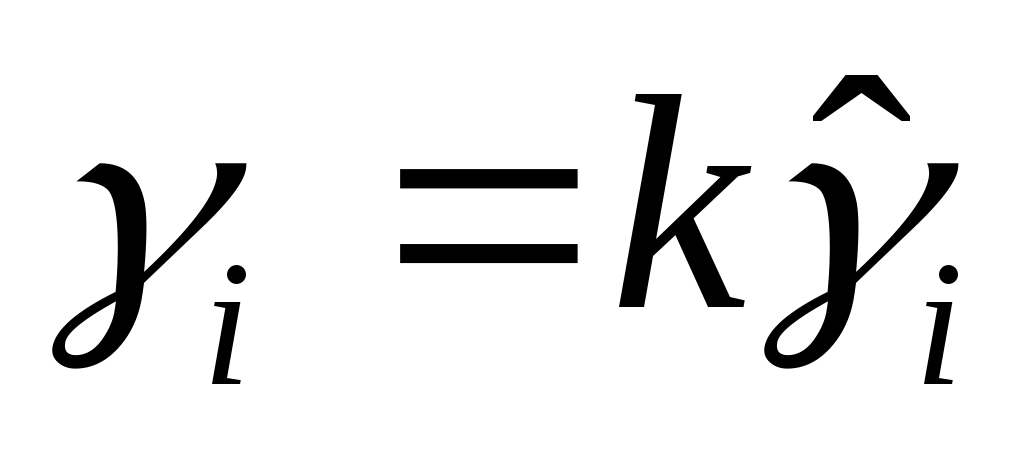 , , 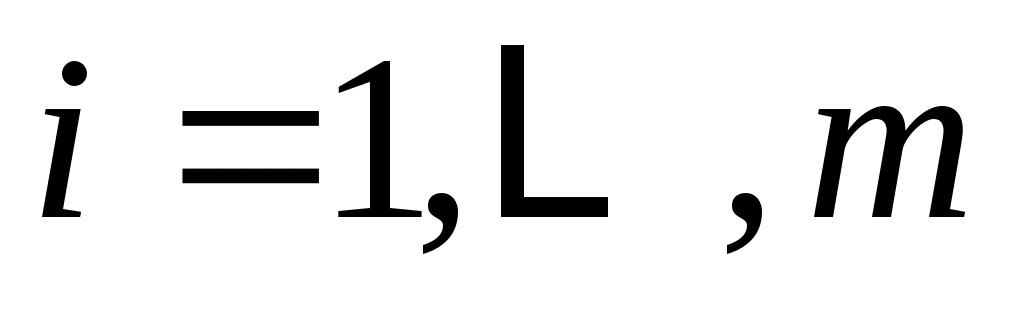
для подходящих полиномов  и и  . Потом . Потом
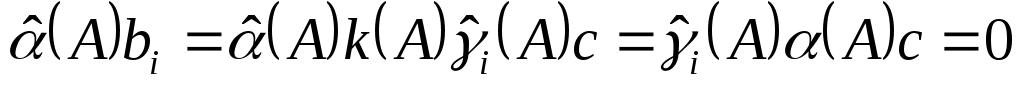 , , 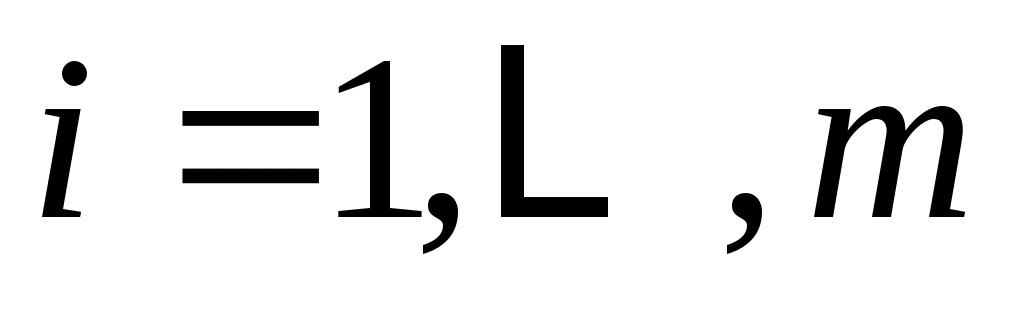 . .
Таким образом 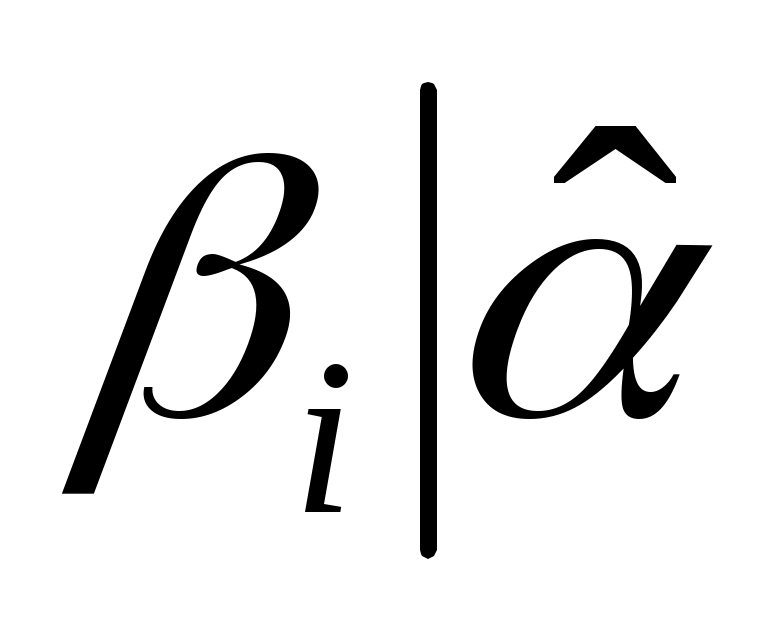 , , 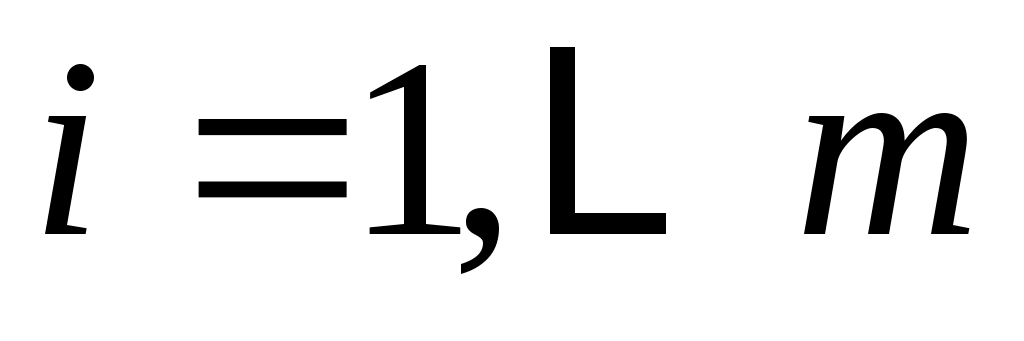 ; следовательно, по определению наименьшим общим кратным, ; следовательно, по определению наименьшим общим кратным,  , то есть , то есть 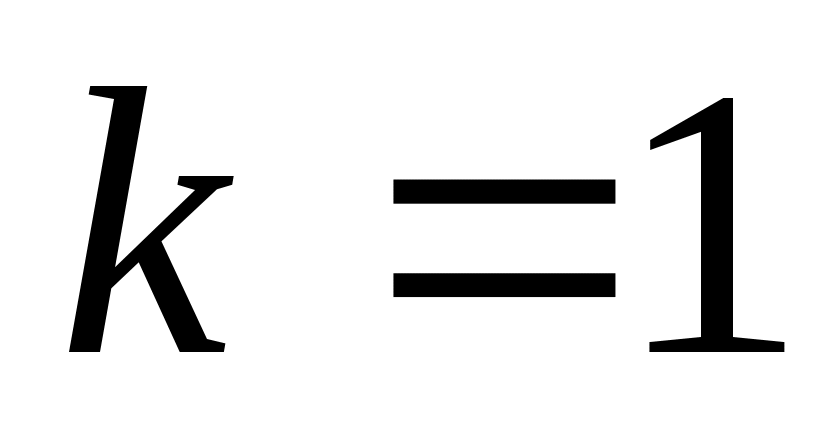 . .
Наконец, обратите внимание, что  и и  взаимно просты тогда и только тогда, когда взаимно просты тогда и только тогда, когда 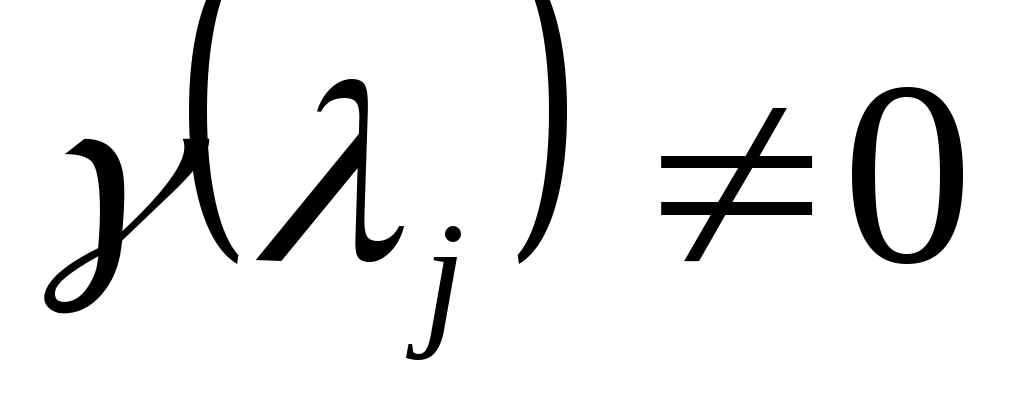 , ,  , где , где  - (комплексные) нули - (комплексные) нули 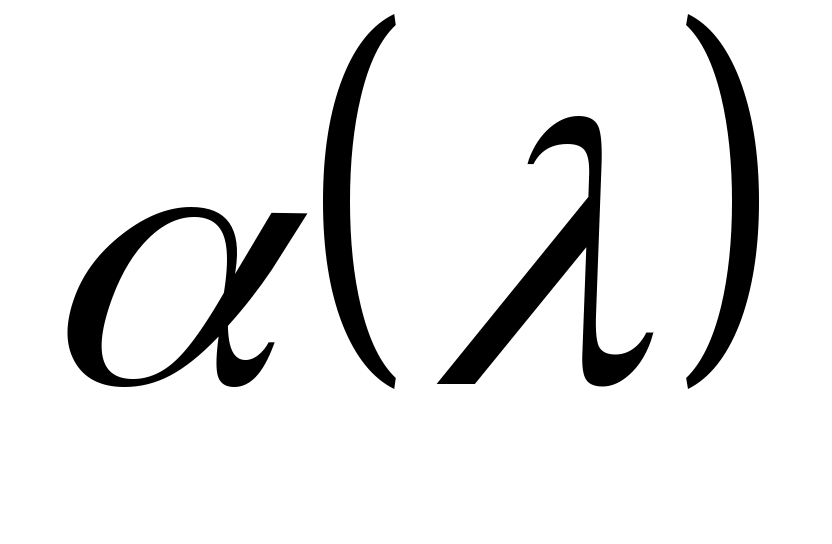 . В силу (5) величины . В силу (5) величины 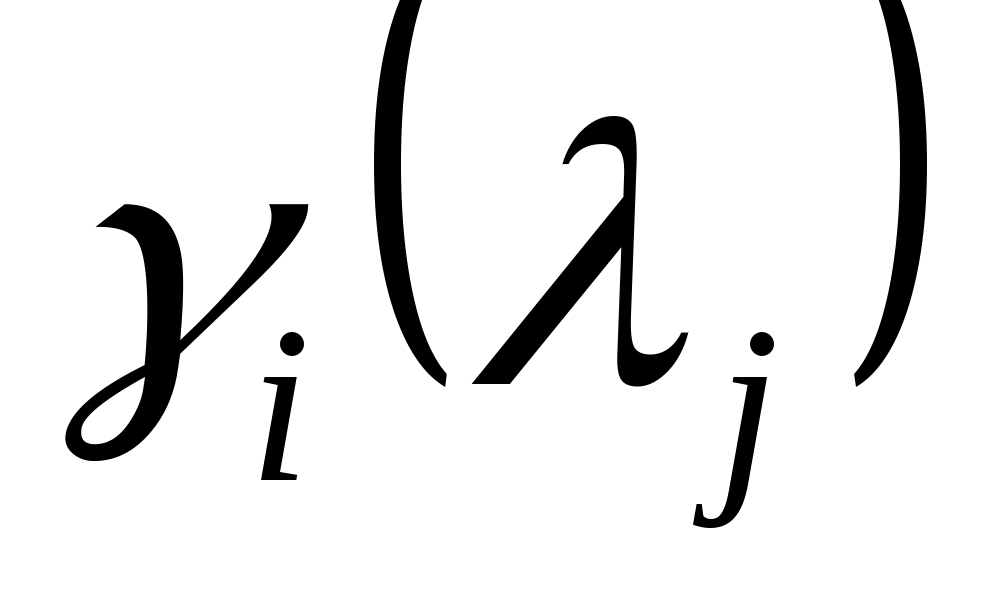 , ,  , не могут все обращаться в нуль для любого , не могут все обращаться в нуль для любого  . Следовательно, числа . Следовательно, числа 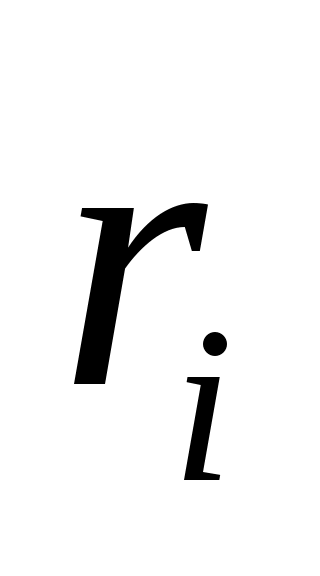 с требуемым свойством существуют. с требуемым свойством существуют.
Следующее наблюдение будет полезно; простое доказательство опущено.
ЛЕММА 4: Если 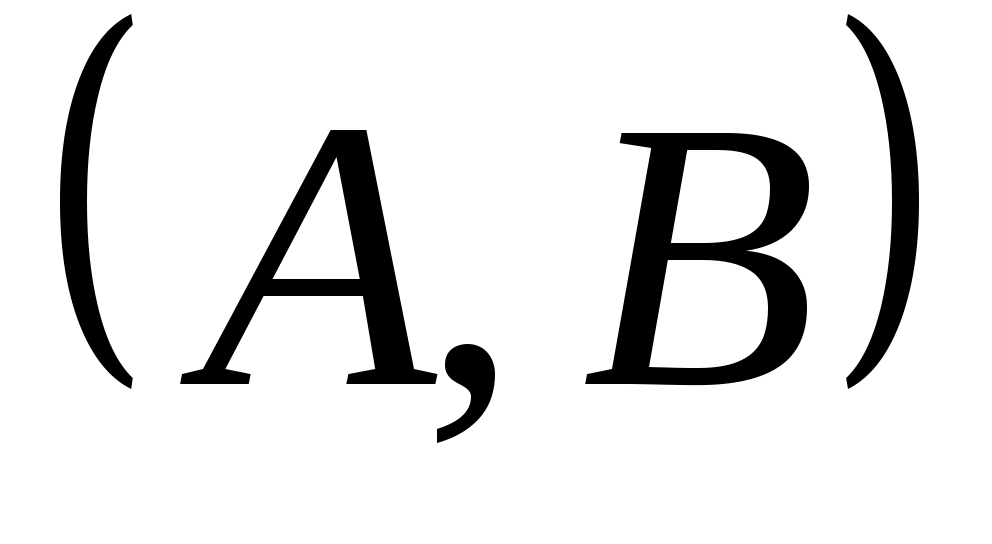 является управляемым и является управляемым и 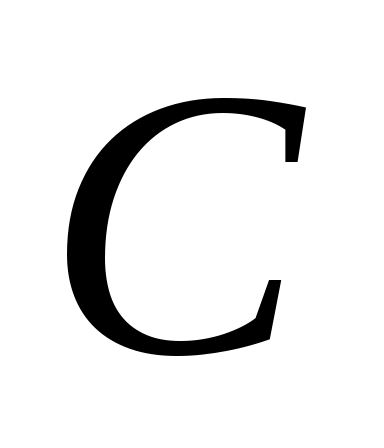 является матрицей является матрицей 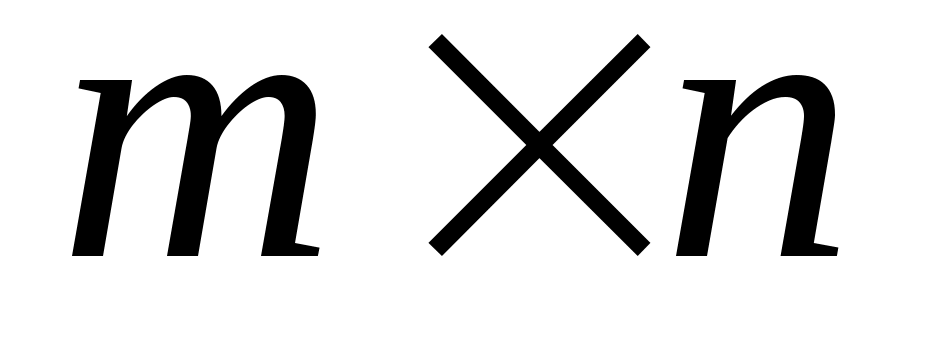 , то , то 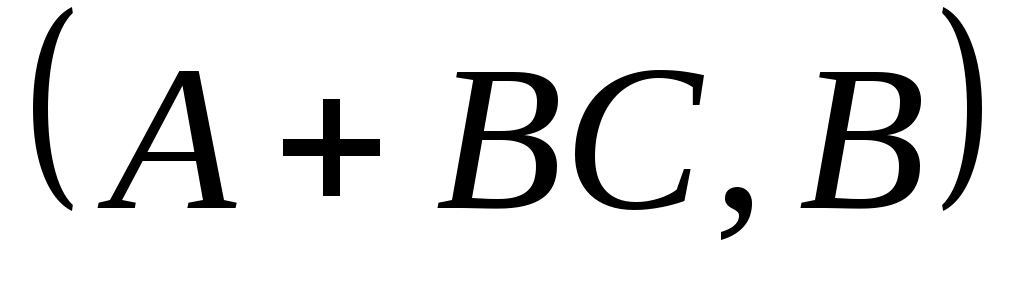 является управляемым. является управляемым.
Также используется концепция соответствия. Пусть 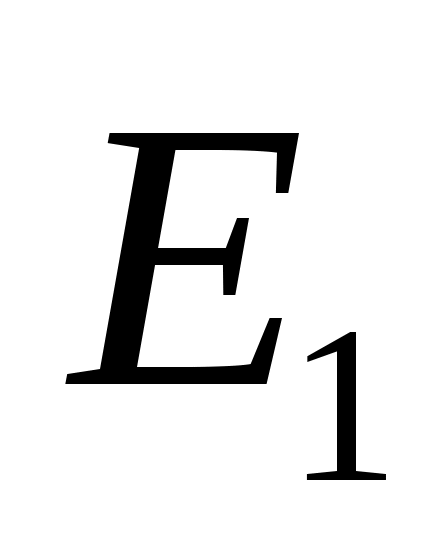 - инвариантное подпространство в - инвариантное подпространство в 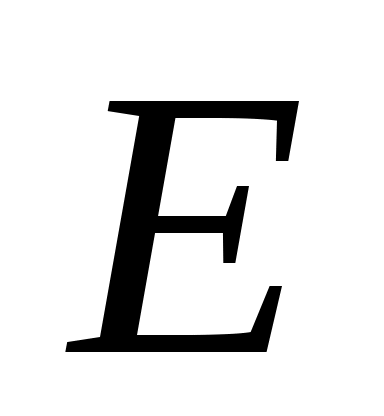 , то есть , то есть 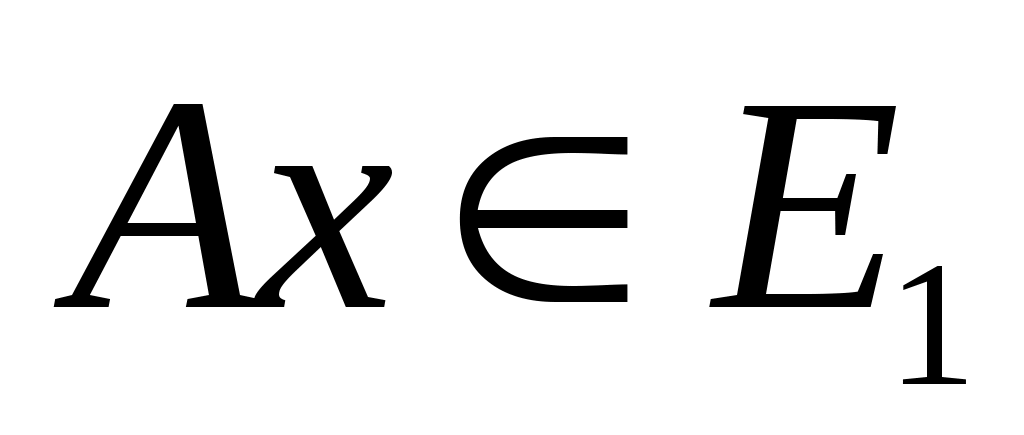 всякий раз, когда всякий раз, когда 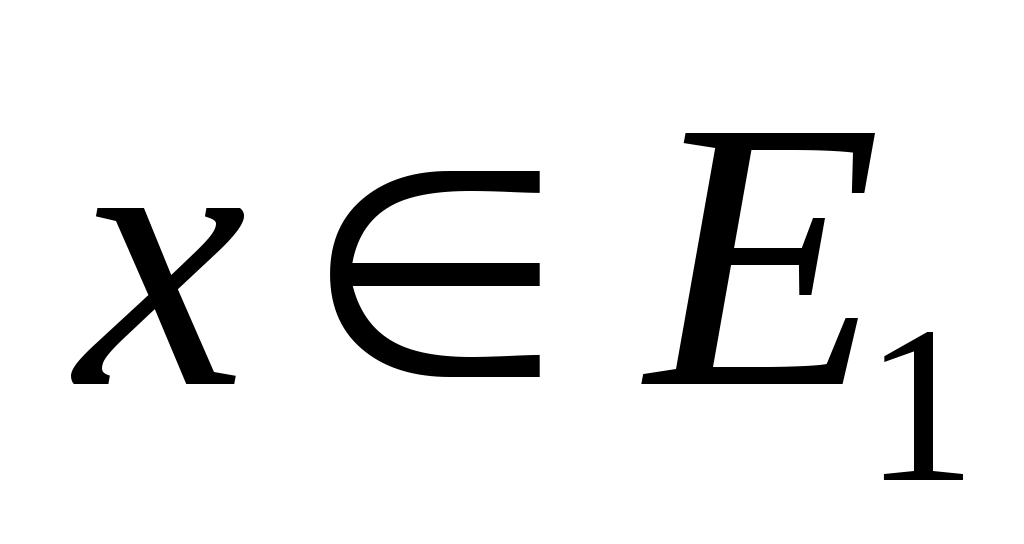 . Подпространство . Подпространство 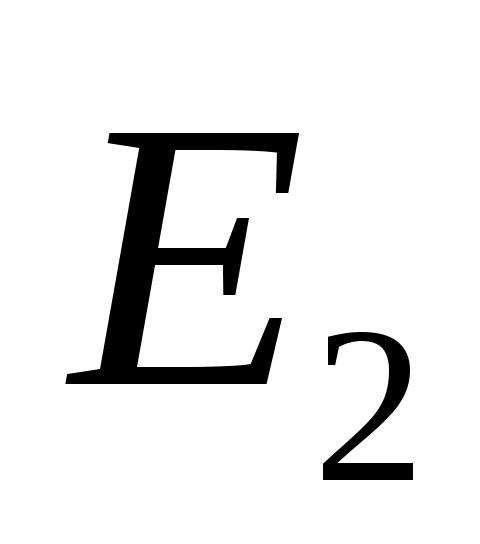 инвариантно инвариантно 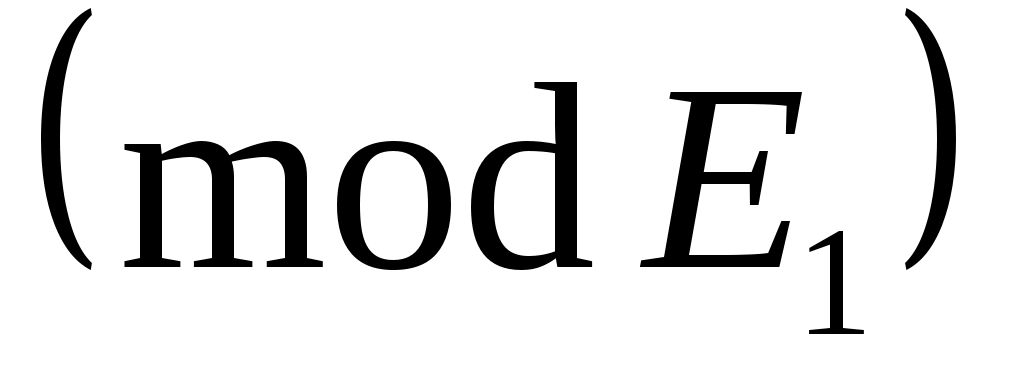 , если , если 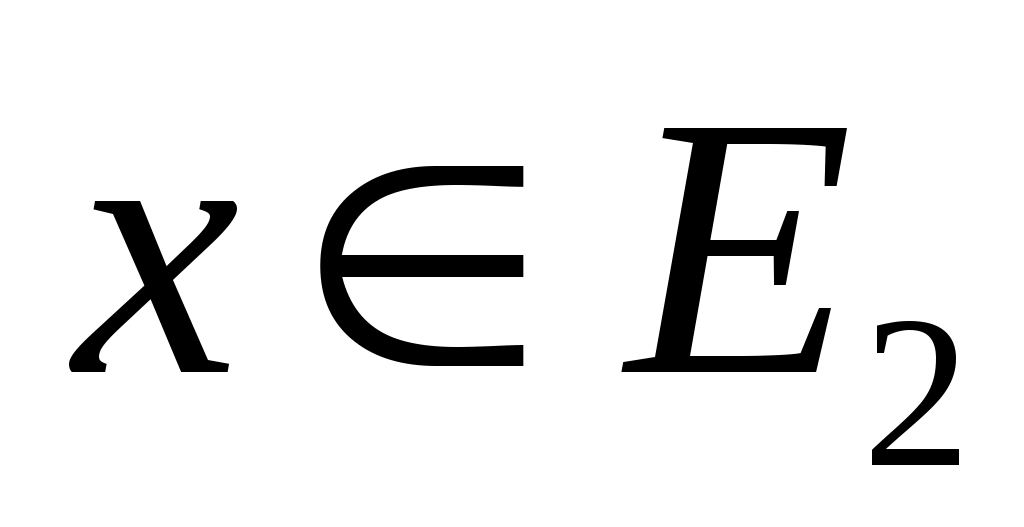 подразумевает подразумевает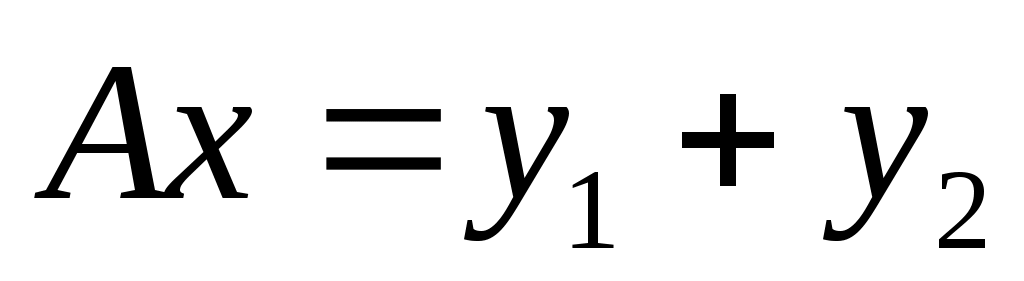 , где , где 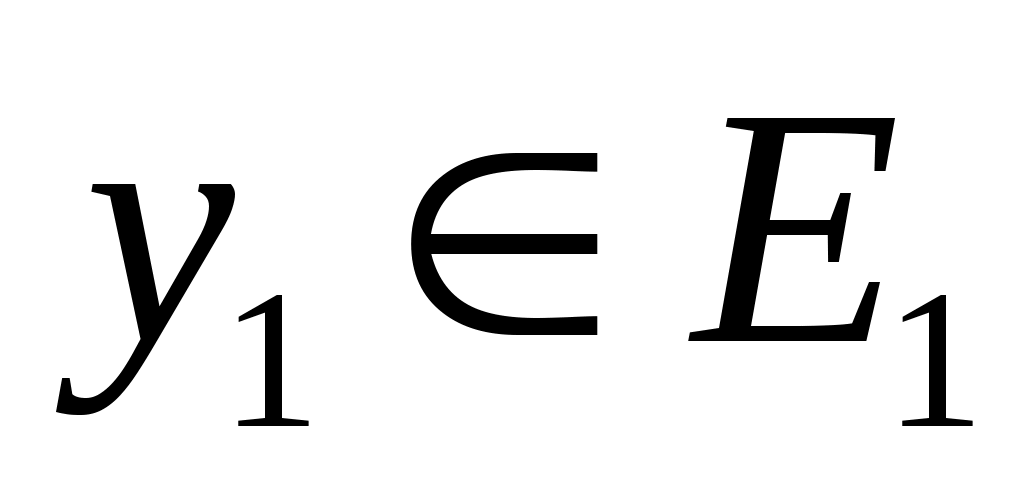 и и 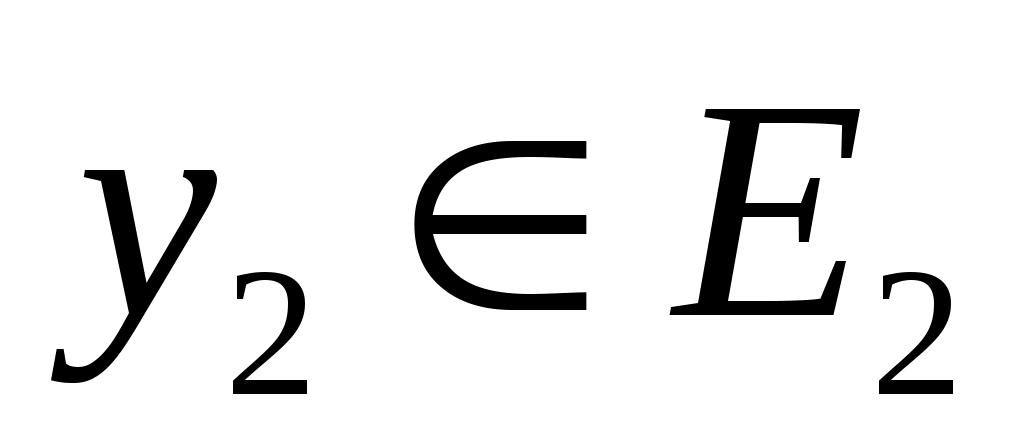 . Напишите . Напишите 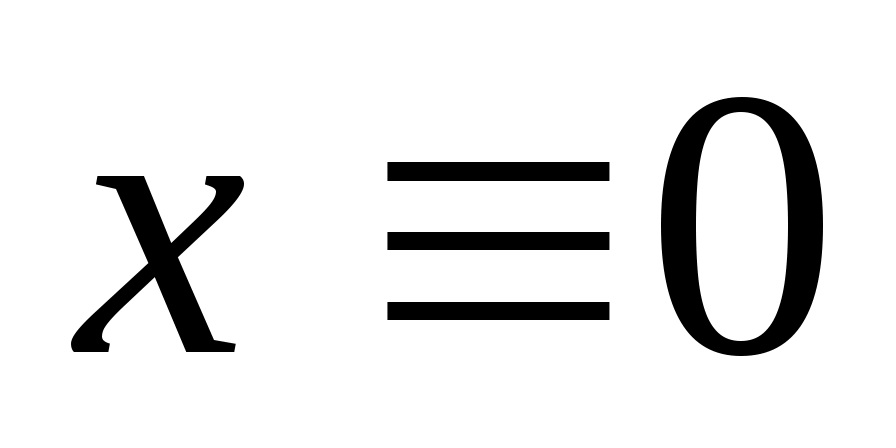 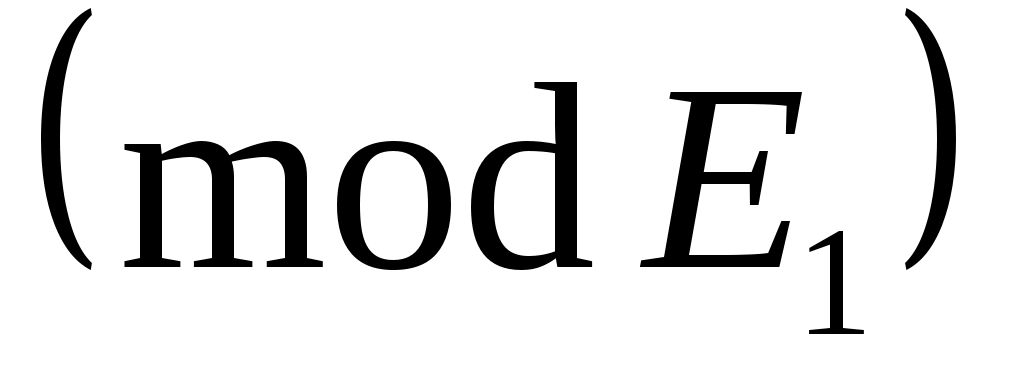 , если , если 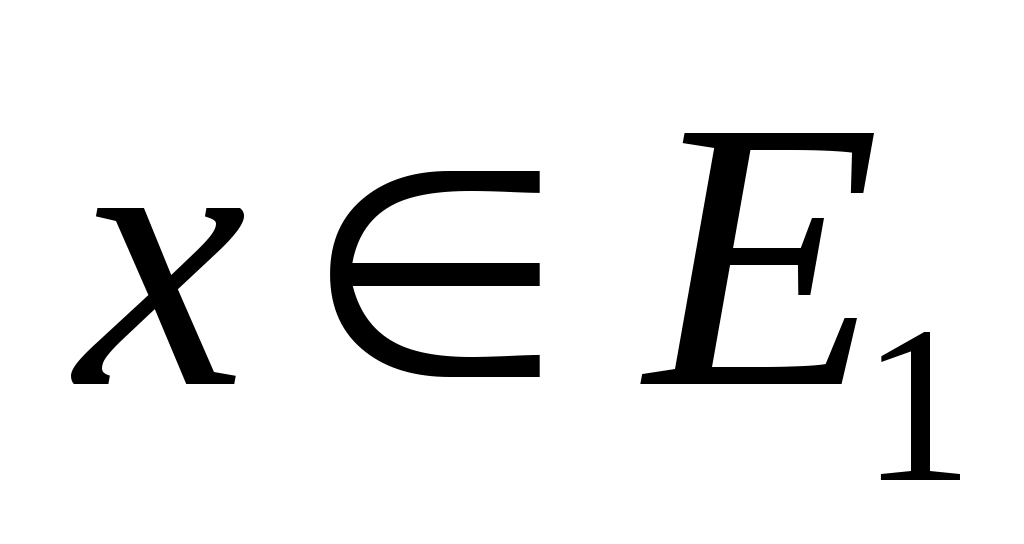 . Векторы . Векторы 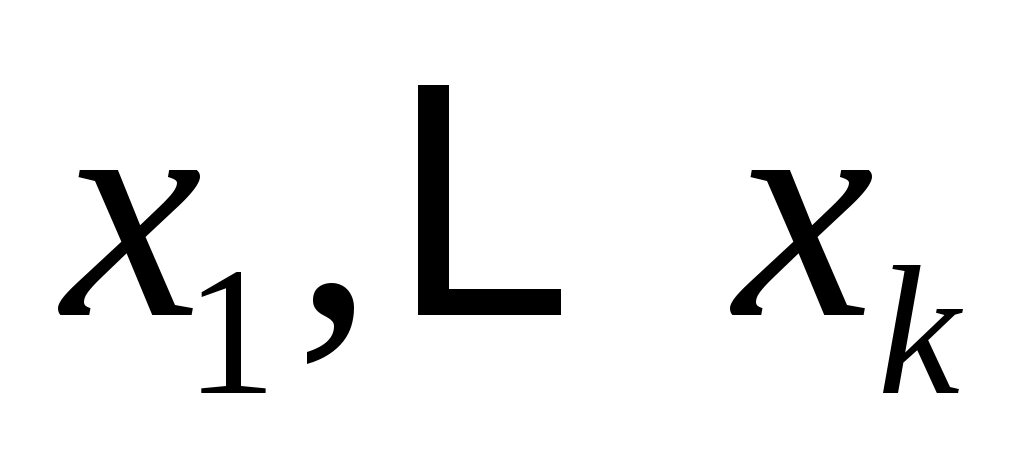 линейно независимы линейно независимы 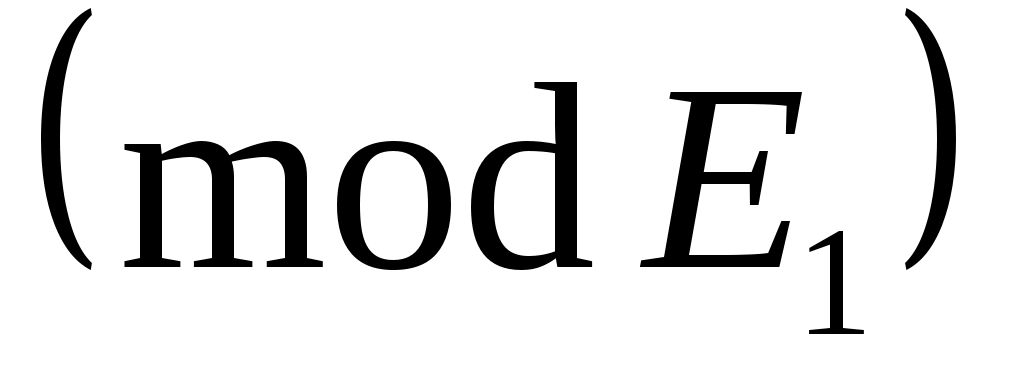 , если из соотношения , если из соотношения 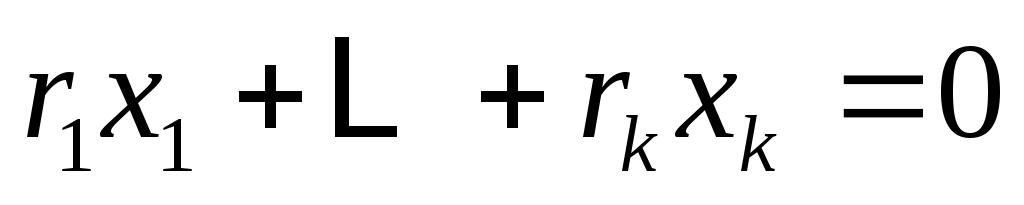 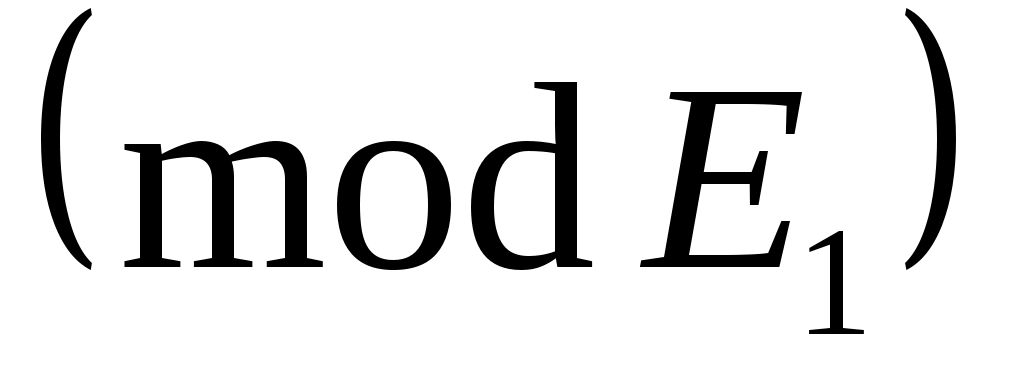 следует следует 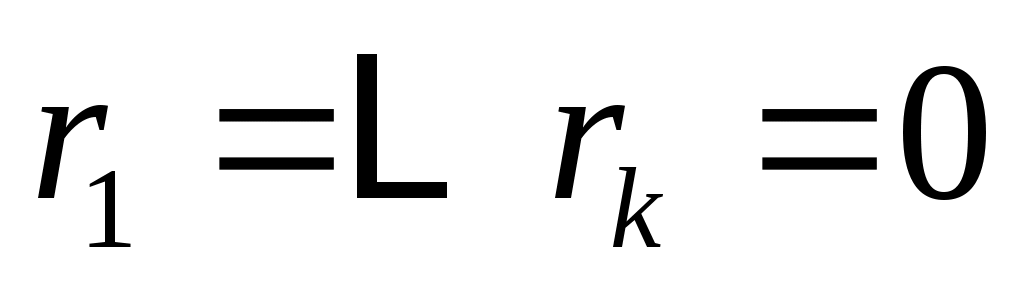 , для всех множеств скаляров , для всех множеств скаляров 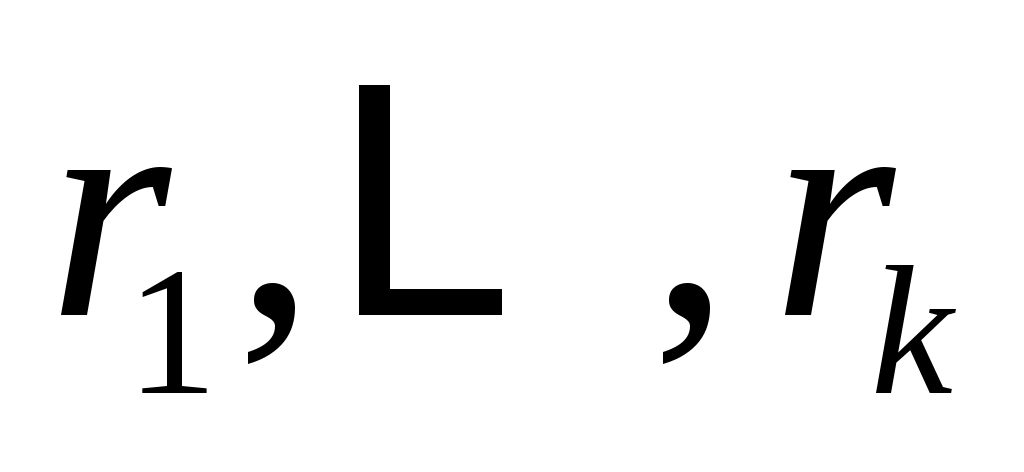 . Для некоторого . Для некоторого 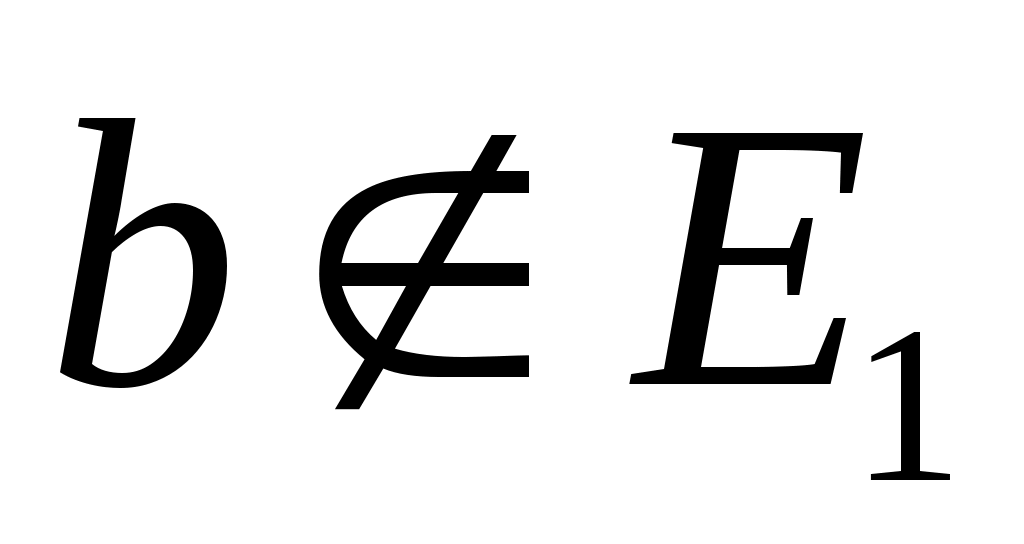 пусть пусть 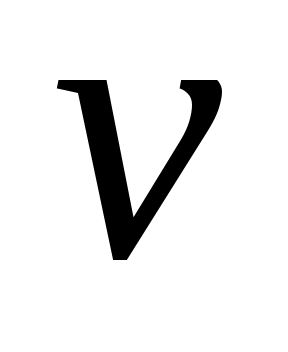 будет наибольшим целым числом таким, чтобы векторы будет наибольшим целым числом таким, чтобы векторы

линейно независимы 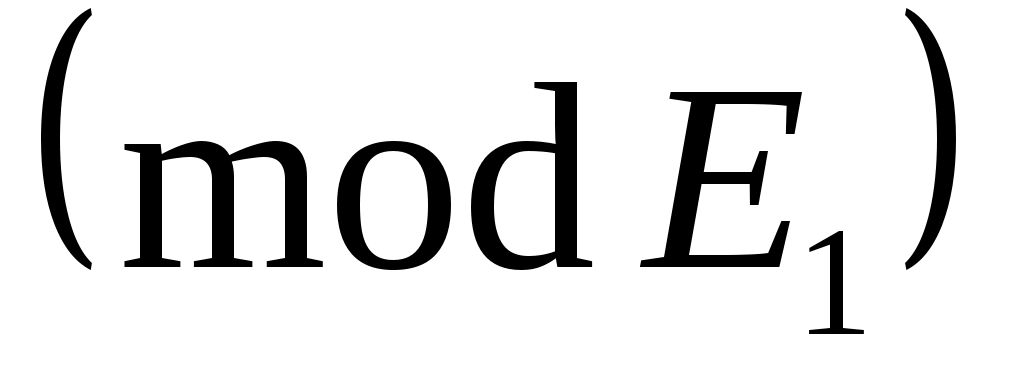 , и пусть , и пусть  будет их пролетом. Тогда будет их пролетом. Тогда  является циклическим является циклическим 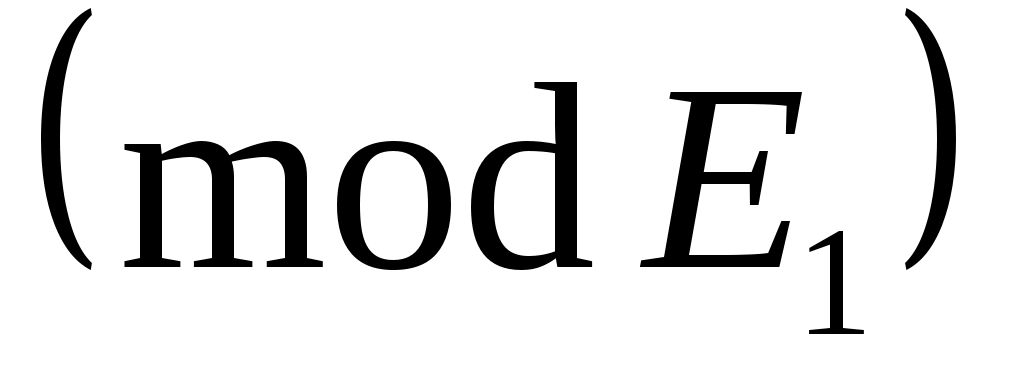 ; ясно, что ; ясно, что  инвариантен инвариантен 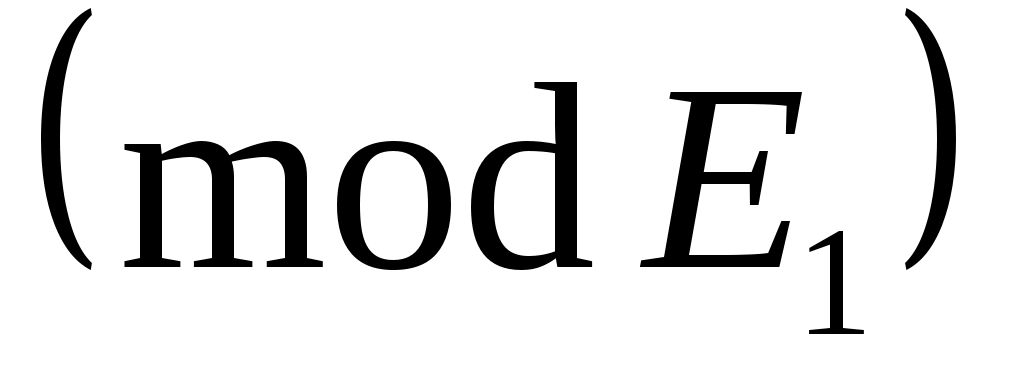 . Относительное минимальный полином для . Относительное минимальный полином для  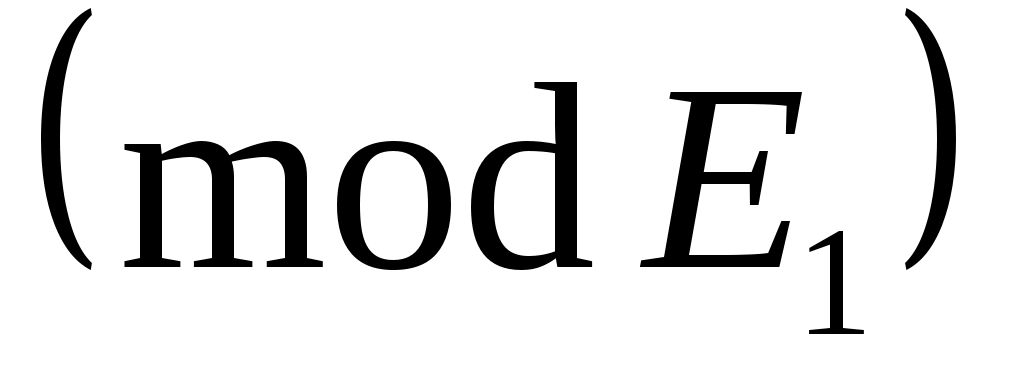 - это (уникальный) нормированный многочлен - это (уникальный) нормированный многочлен 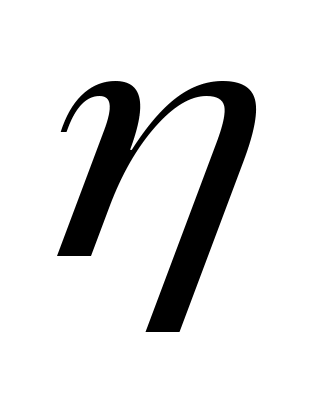 наименьшей степени такой, что наименьшей степени такой, что 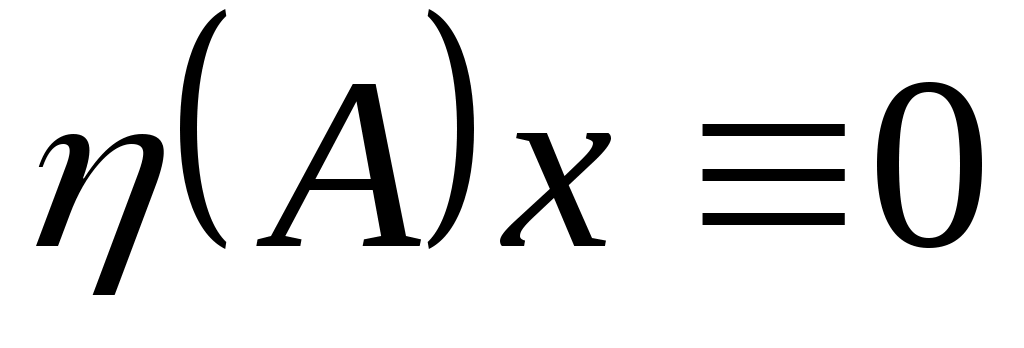 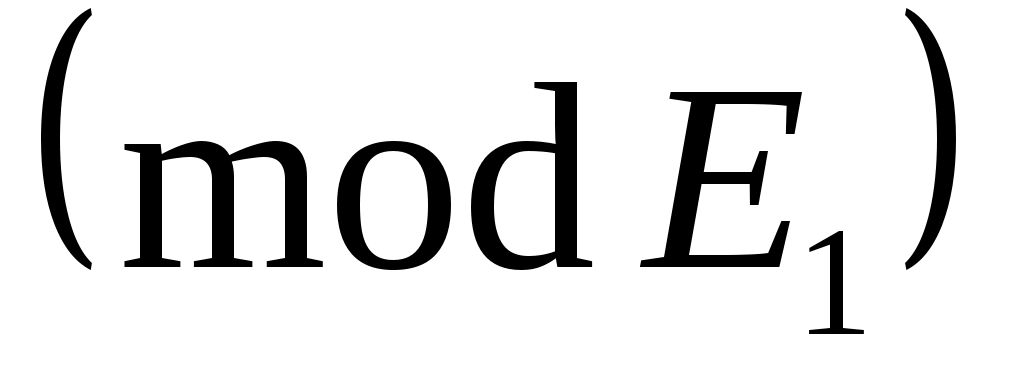 для всех для всех 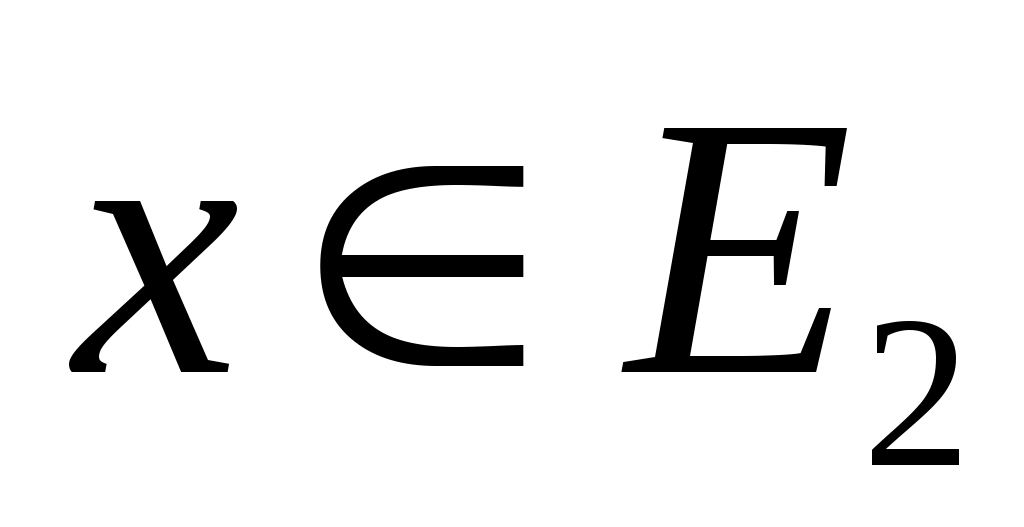 . .
2) Доказательство необходимости: Теперь можно доказать необходимость. Пусть 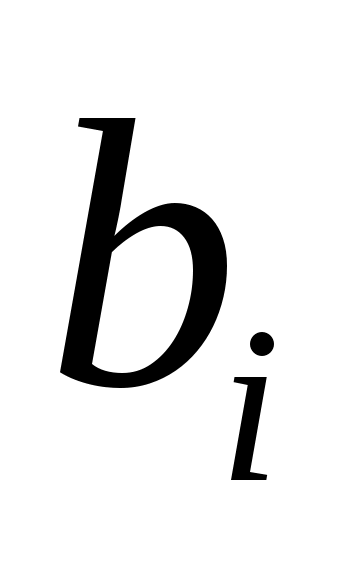 обозначает обозначает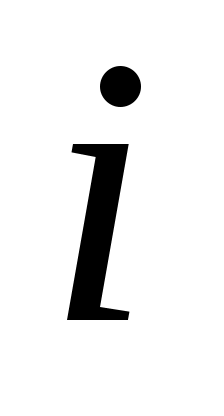 -й столбец -й столбец 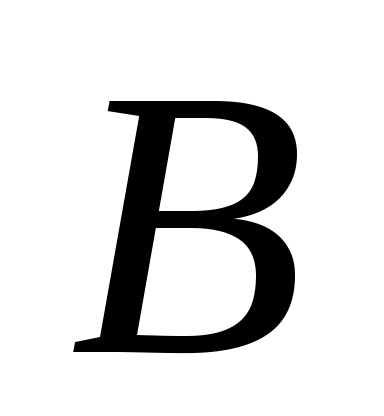 : :
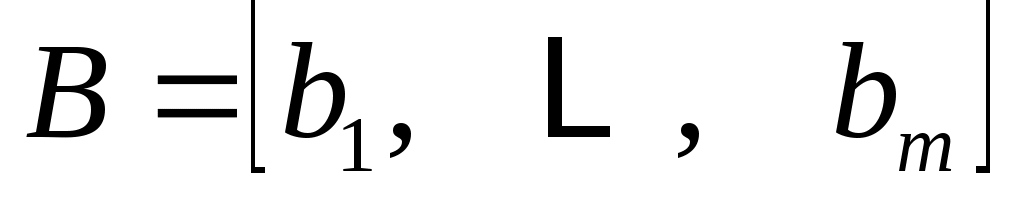 . .
Пусть 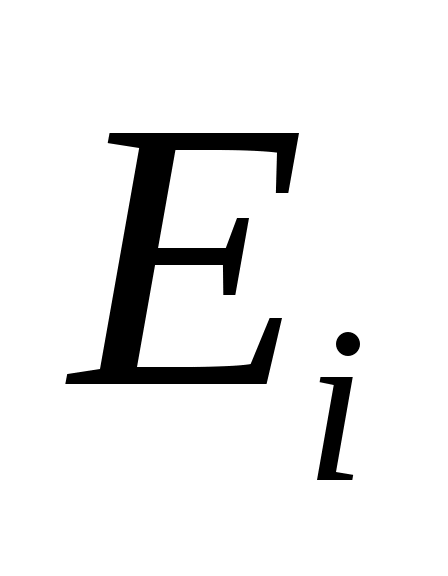 быть циклическим подпространством, порожденным быть циклическим подпространством, порожденным 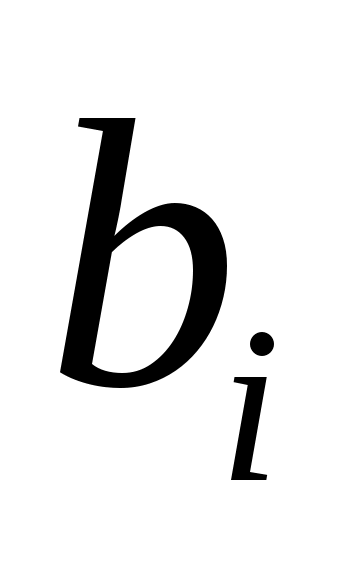 , и положить , и положить 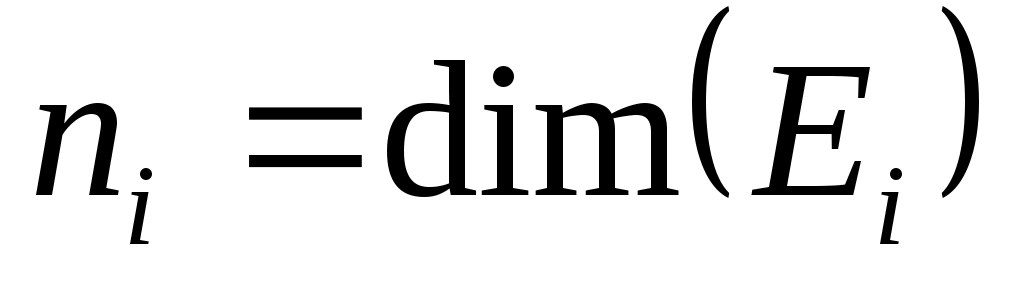 . Поскольку . Поскольку 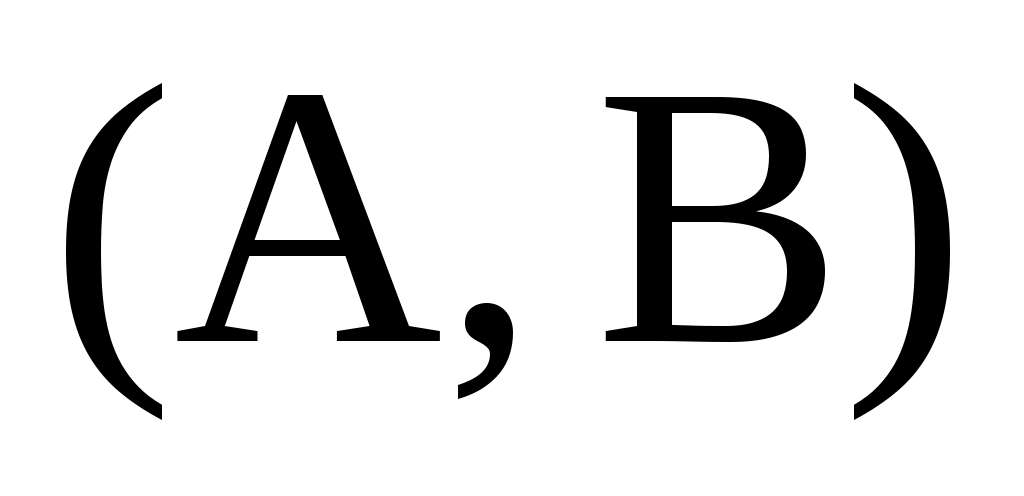 является управляемым, является управляемым,
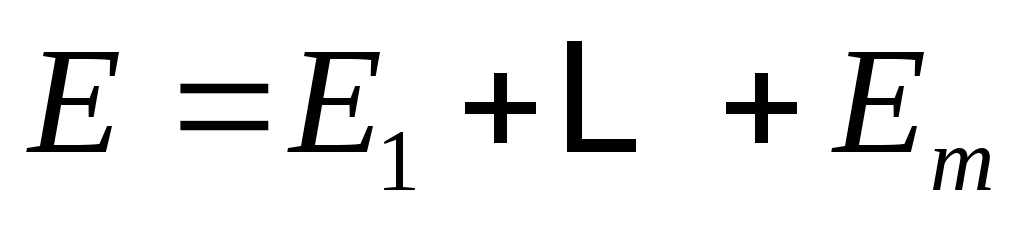
но в целом 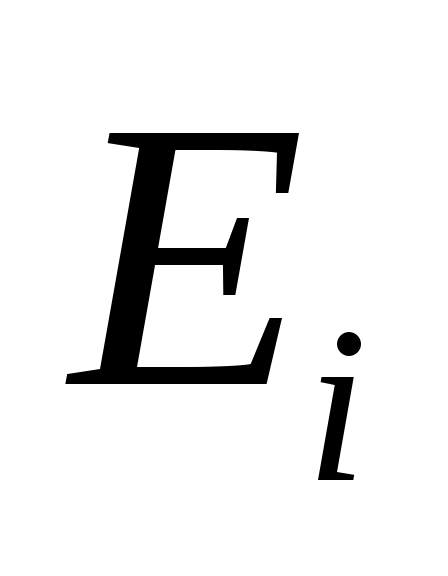 не являются независимыми. Тем не менее, не являются независимыми. Тем не менее, 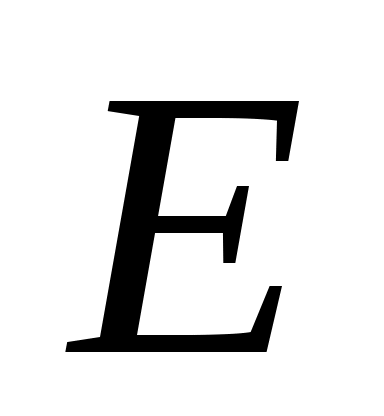 можно записать как прямую сумму можно записать как прямую сумму
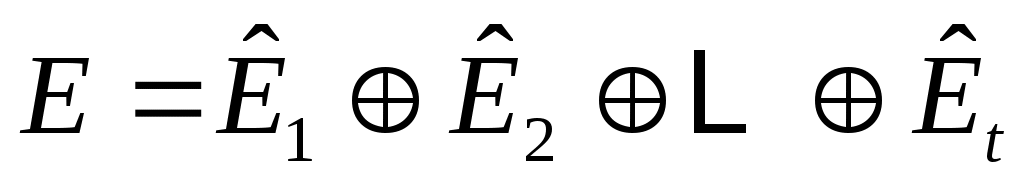 , ,  (6) (6)
где определенные подпространства  . Чтобы увидеть это, предположим, что . Чтобы увидеть это, предположим, что 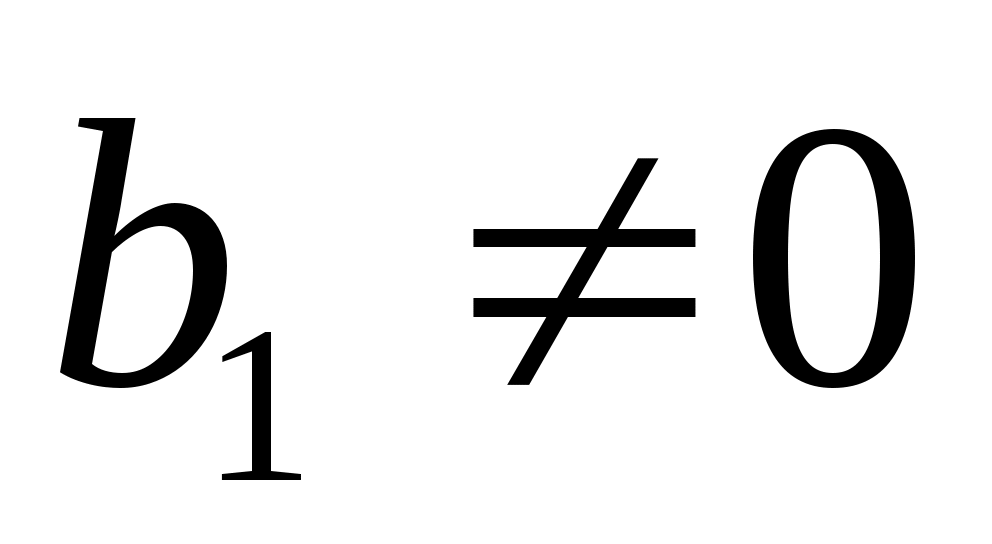 , и определим , и определим 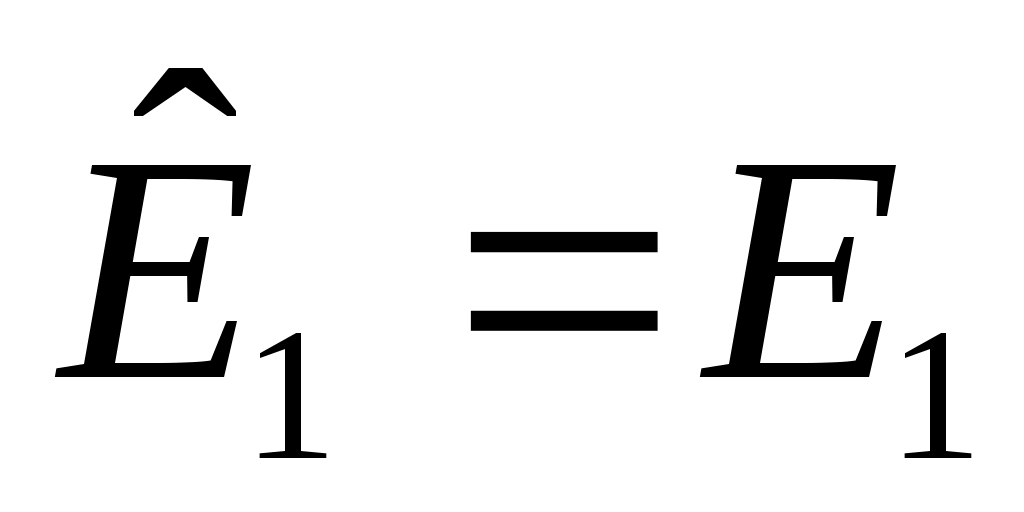 . Если . Если 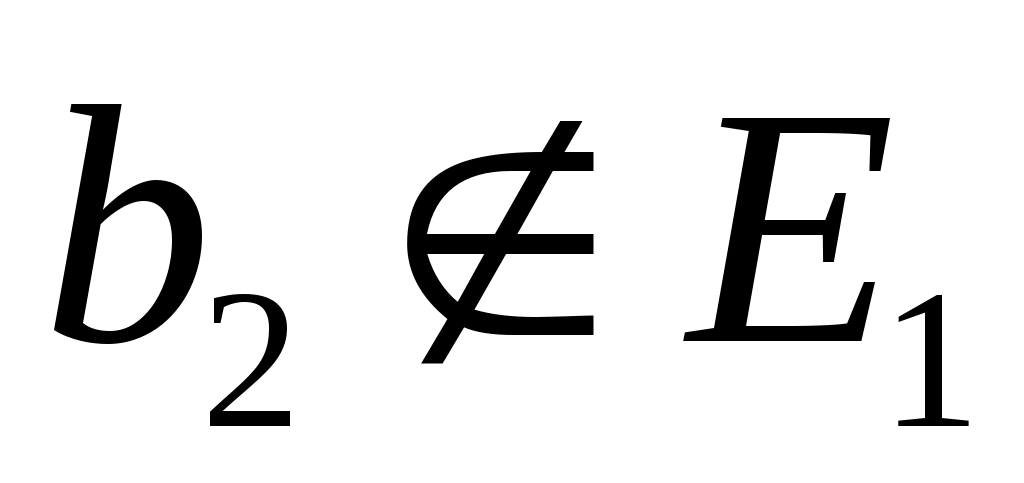 то пусть то пусть 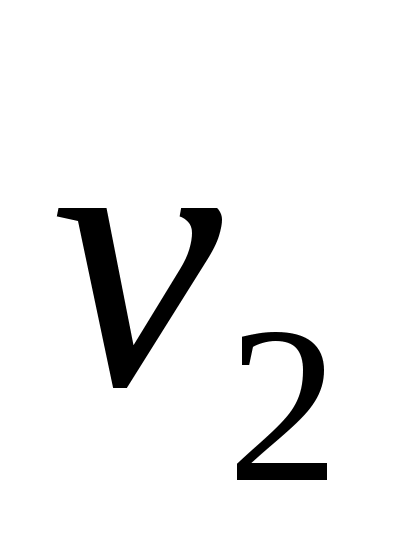 , , 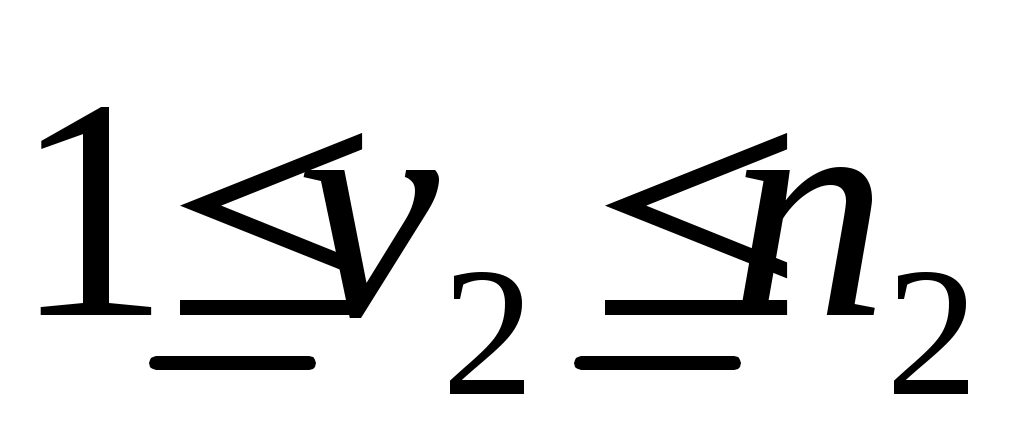 , будет наибольшим целым числом, таким, что векторы , будет наибольшим целым числом, таким, что векторы
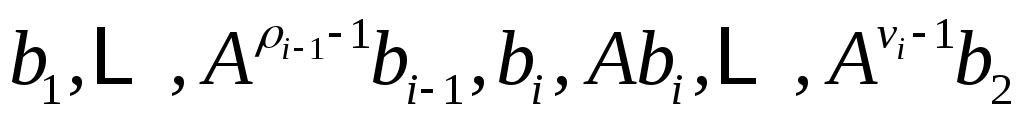
линейно независимы, и пусть 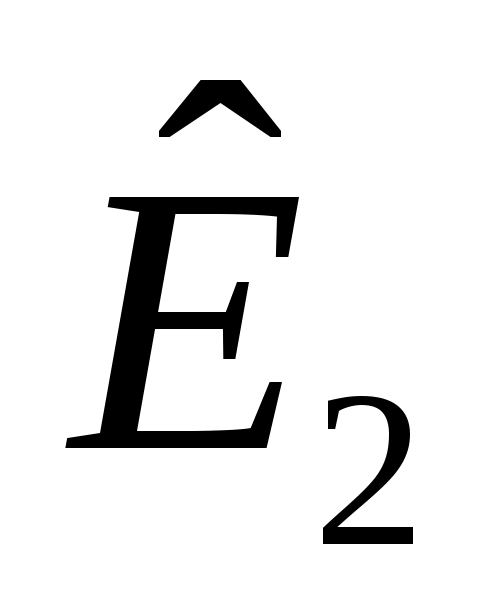 будет пролетом будет пролетом 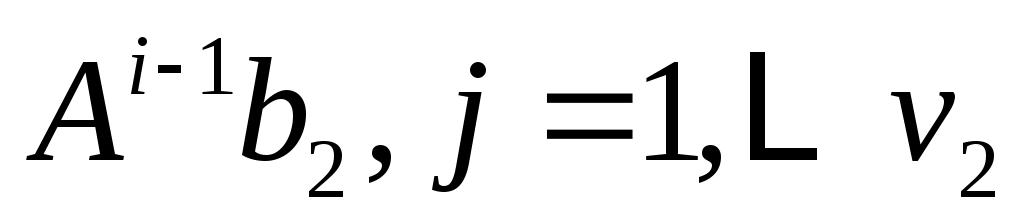 . Тогда . Тогда 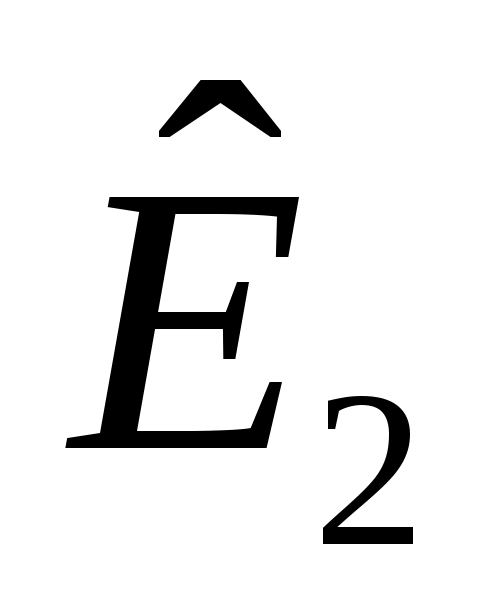 является циклическим является циклическим 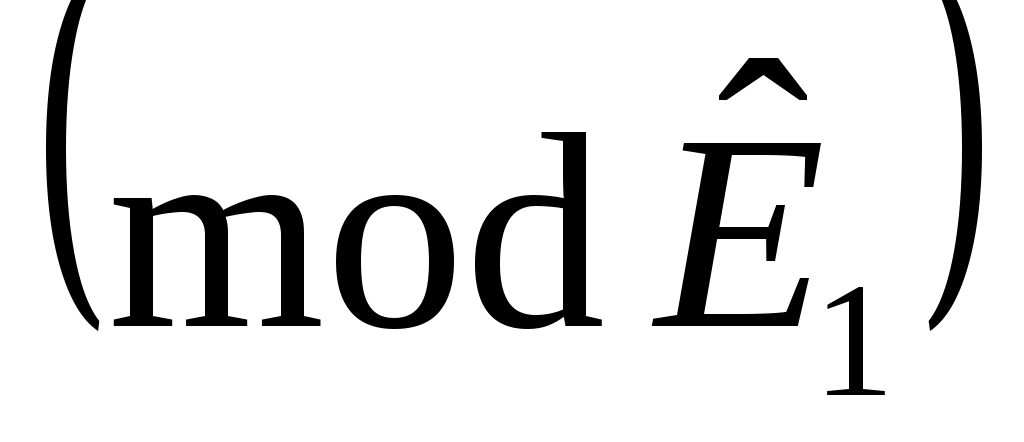 , с относительным минимальный полином степени , с относительным минимальный полином степени 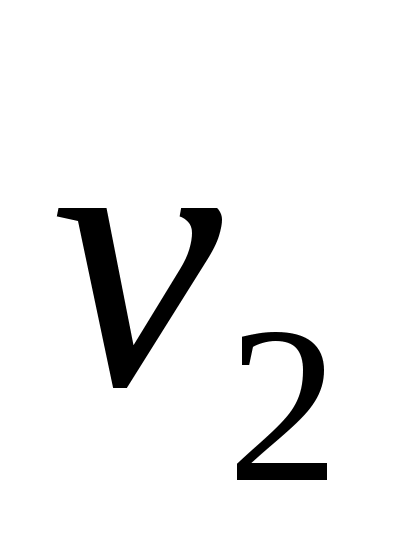 . Продолжая таким образом, для . Продолжая таким образом, для 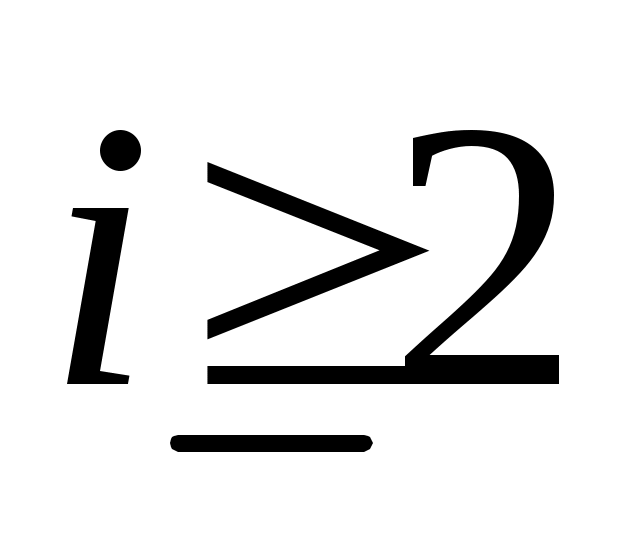 определим определим 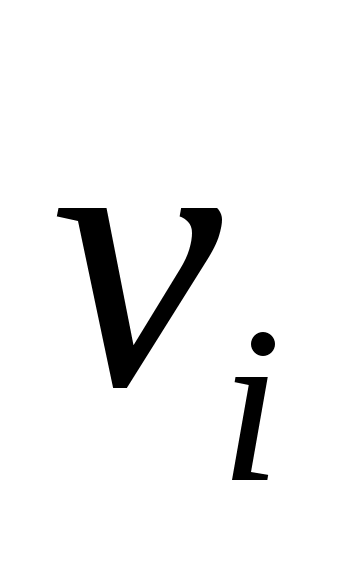 , , 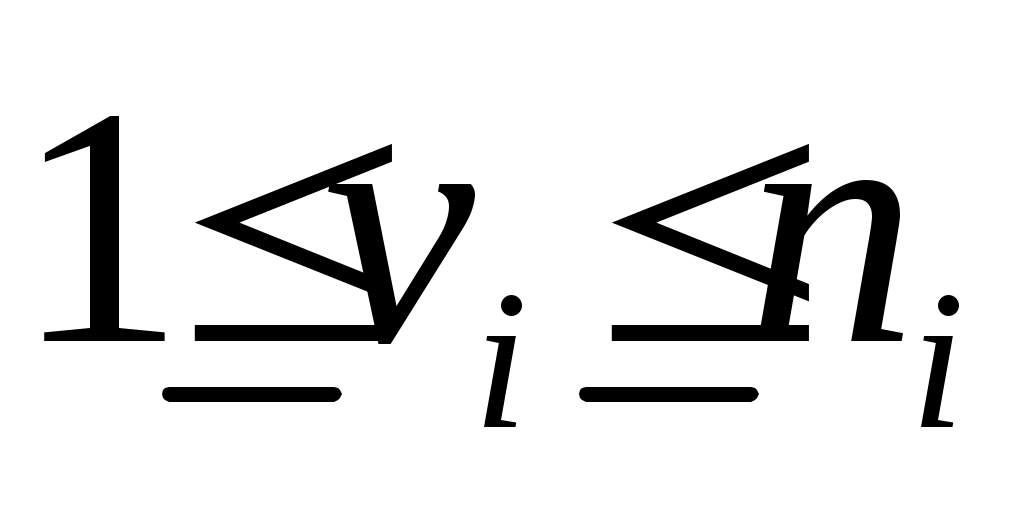 , чтобы быть наибольшим целым числом таким, чтобы векторы. , чтобы быть наибольшим целым числом таким, чтобы векторы.
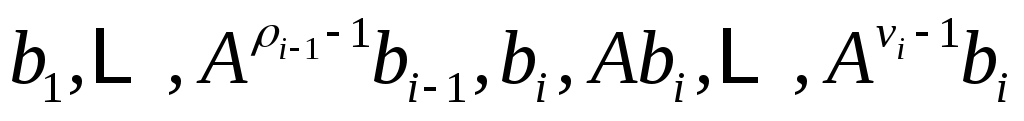
линейно независимы, и пусть 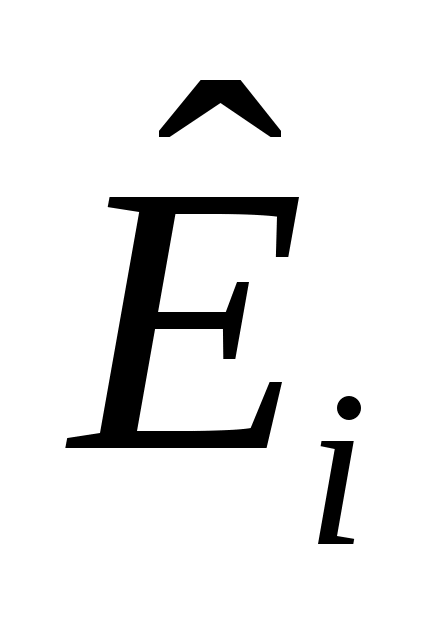 будет пролетом будет пролетом  . Тогда . Тогда 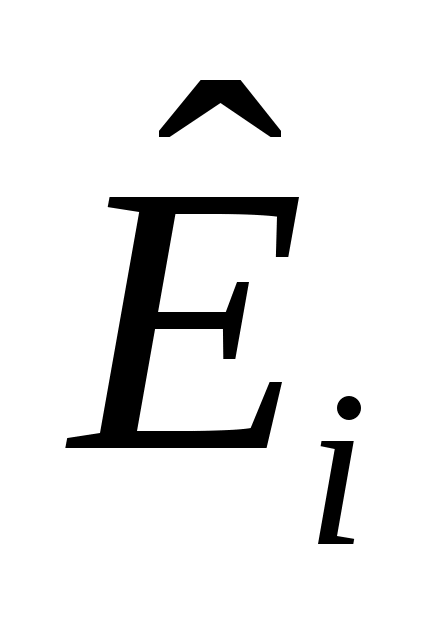 циклическое циклическое 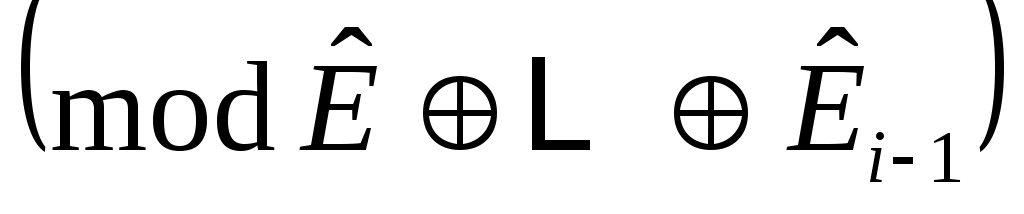 с относительным минимальный полином степени с относительным минимальный полином степени  . Если на любом этапе . Если на любом этапе 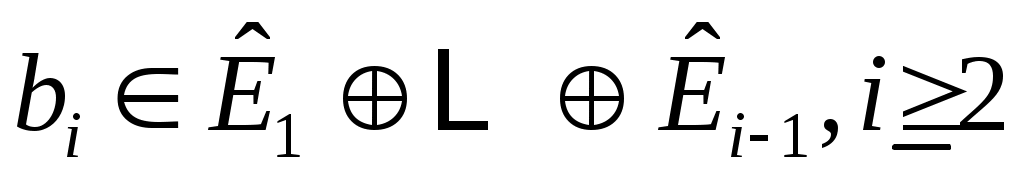 , то , то 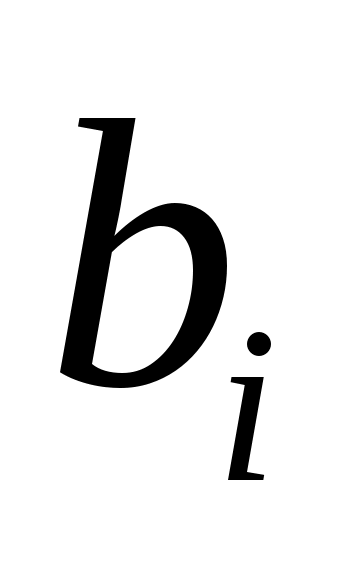 пропускается. Переупорядочив столбцы пропускается. Переупорядочив столбцы 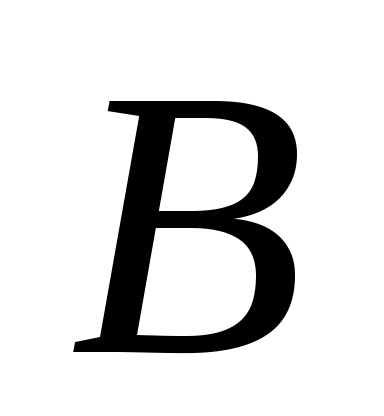 , если это необходимо, можно организовать, что для , если это необходимо, можно организовать, что для 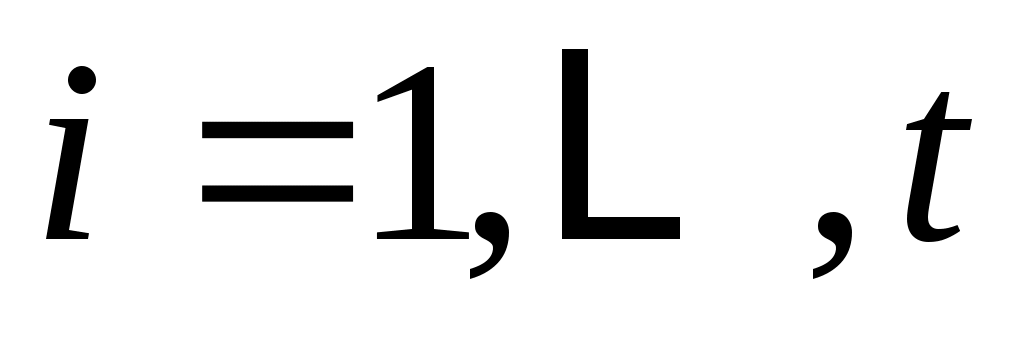 векторы векторы 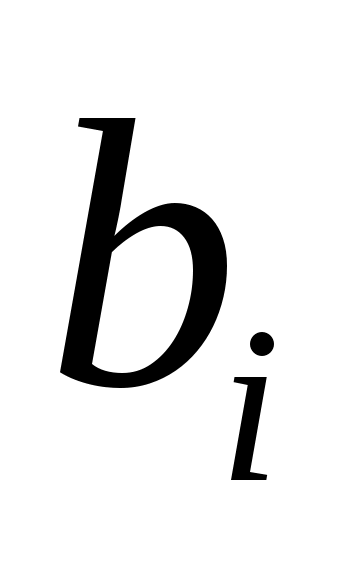 порождают независимые подпространства порождают независимые подпространства 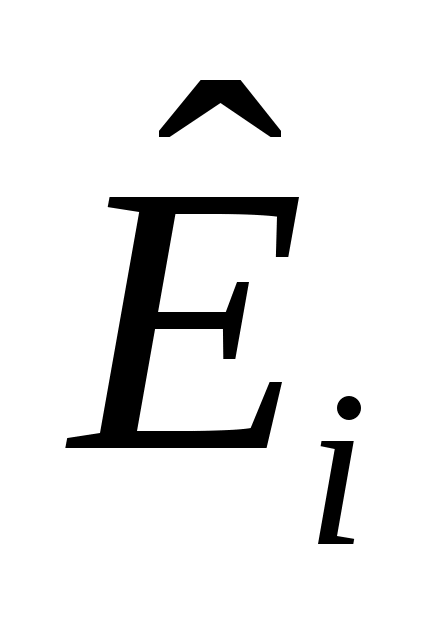 , где либо , где либо 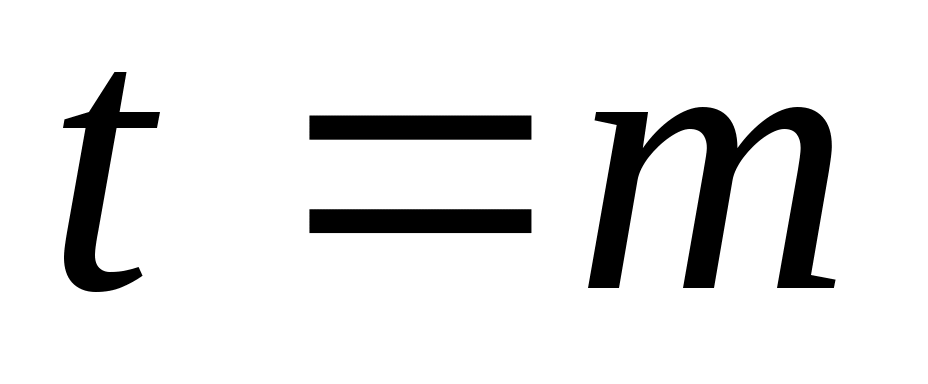 , либо , либо 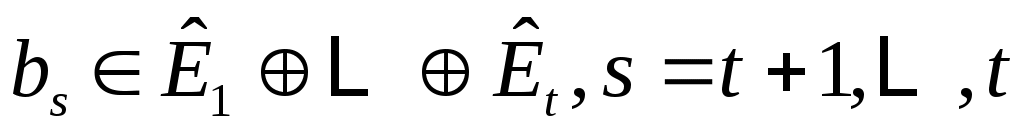 . Поскольку . Поскольку 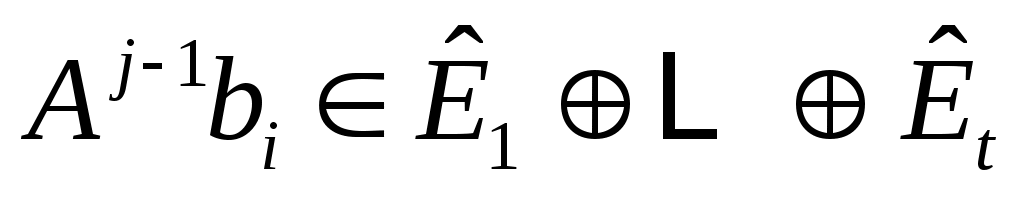 , если , если 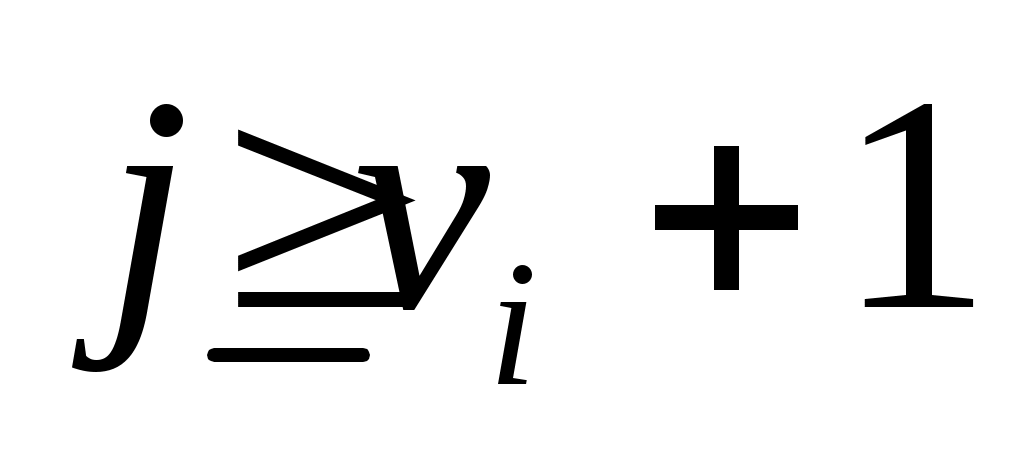 , ,  , то следует, что (6) верно и, следовательно, , то следует, что (6) верно и, следовательно, 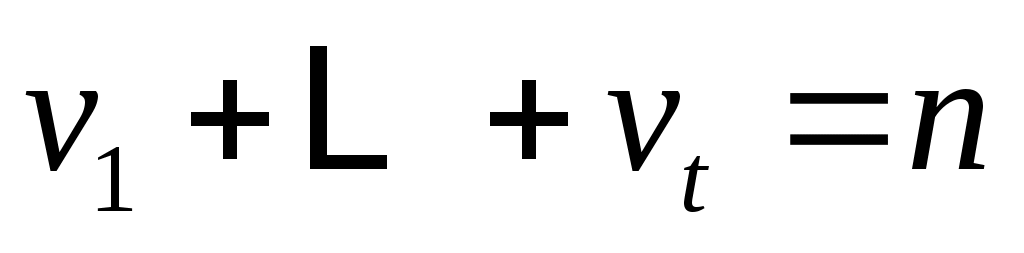 . .
Далее  трансформируется в удобную стандартную форму. трансформируется в удобную стандартную форму.
Позволять
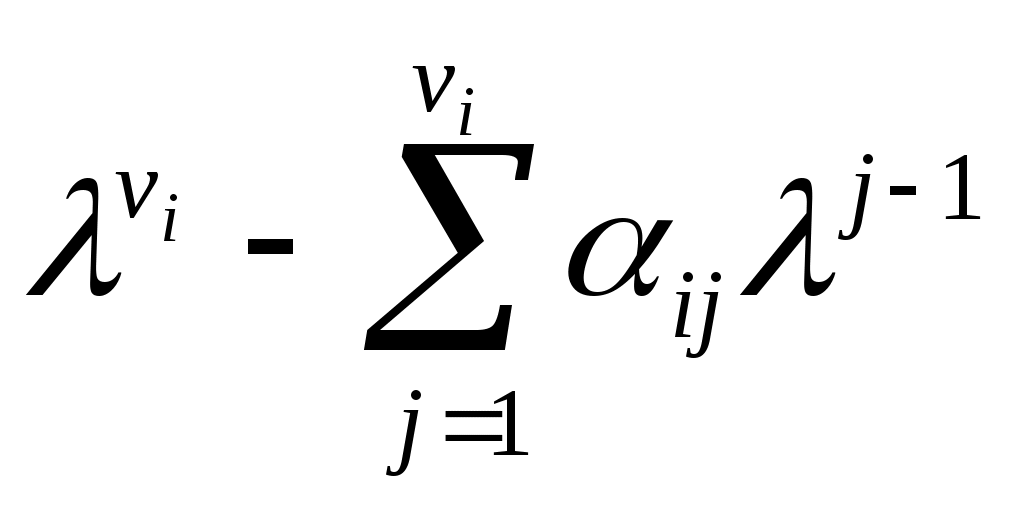 , , 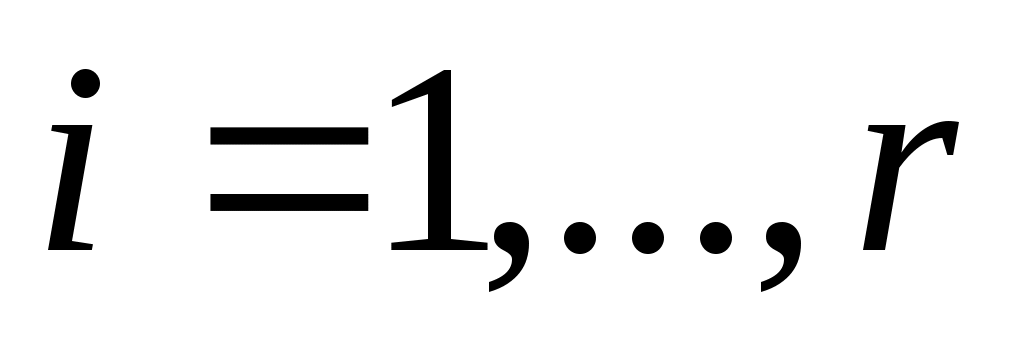 (7) (7)
быть относительным минимальный полином для 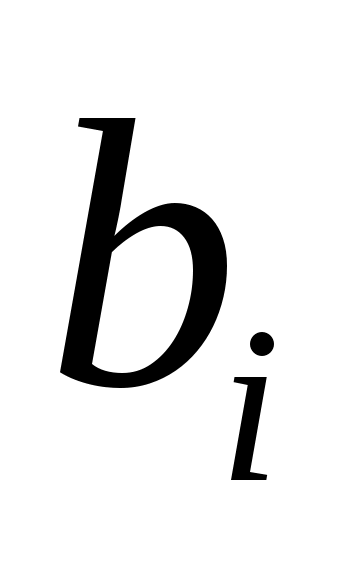 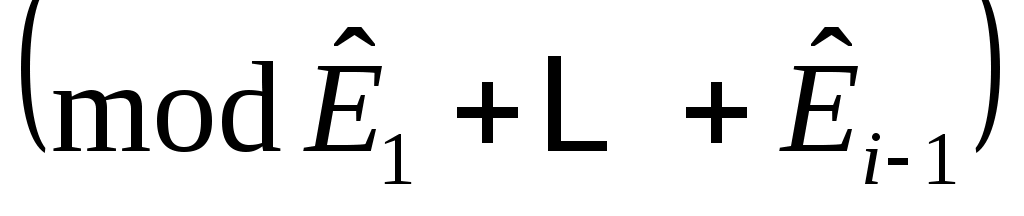 или абсолютным минимальный полином для или абсолютным минимальный полином для 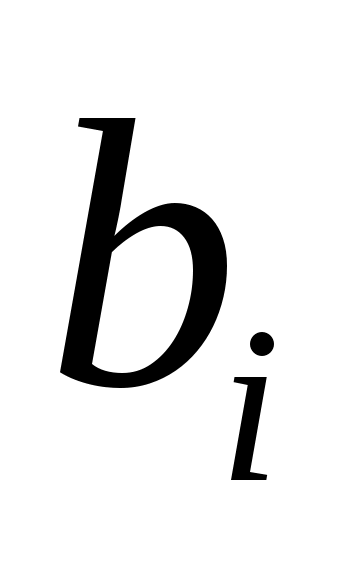 в случае в случае 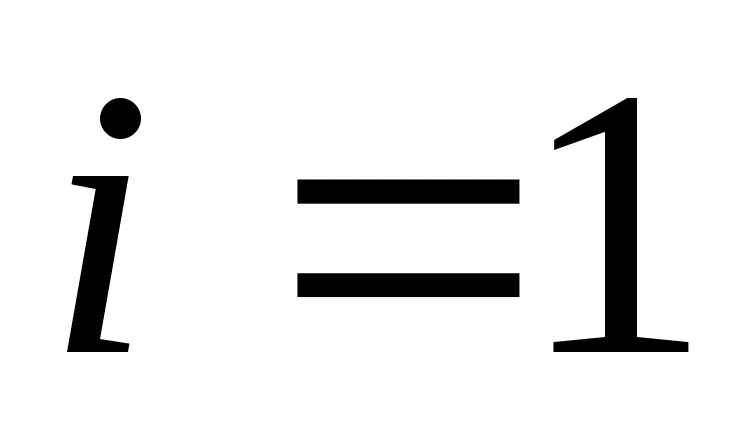 . Следуя Лангенхопу [2], ввести векторы . Следуя Лангенхопу [2], ввести векторы
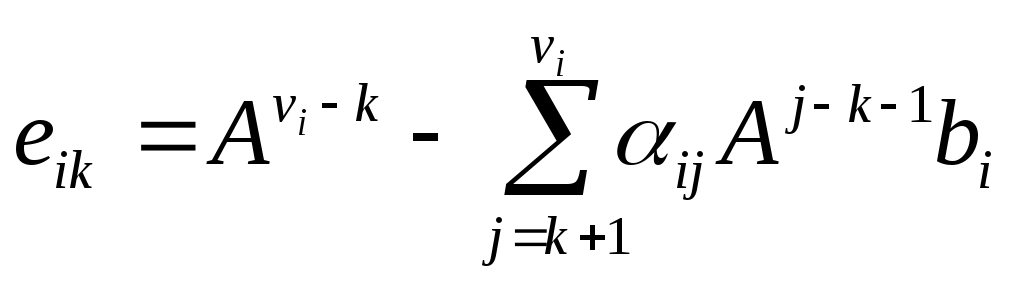 , , 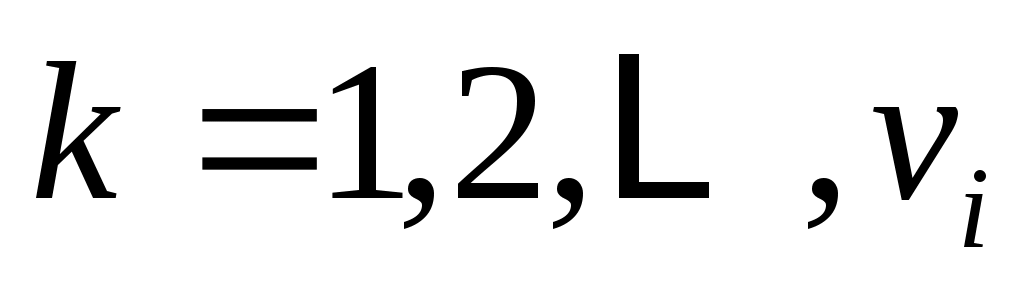 , , 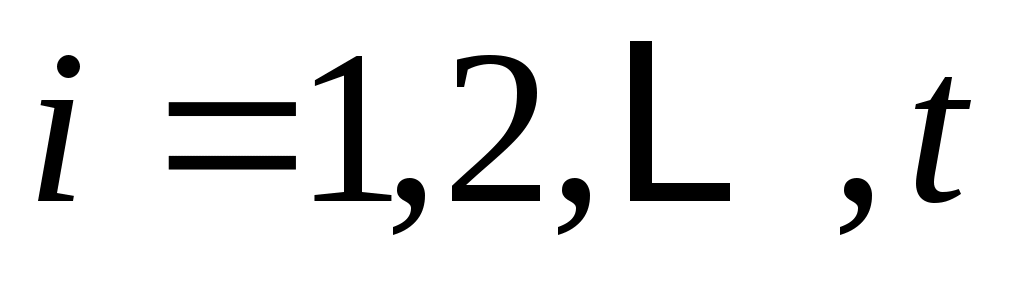 (8а) (8а)
где суммирование не появляется в случае 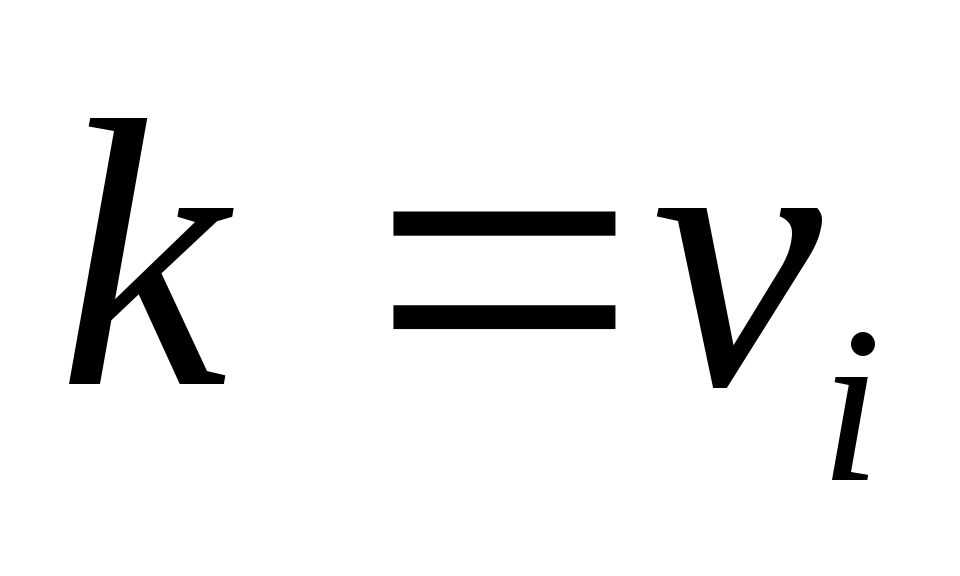 ; то есть, ; то есть,
 , , 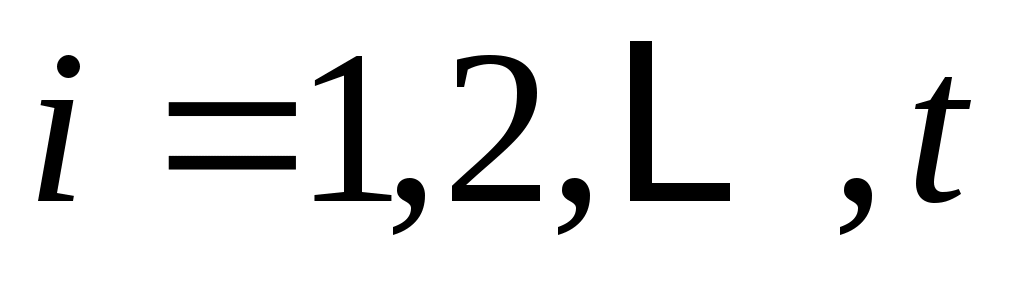 . (8b) . (8b)
Понятно, что для каждого 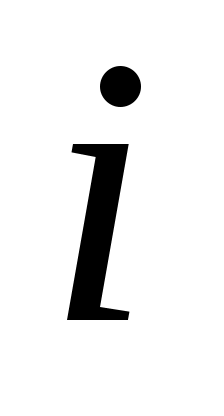 векторы векторы 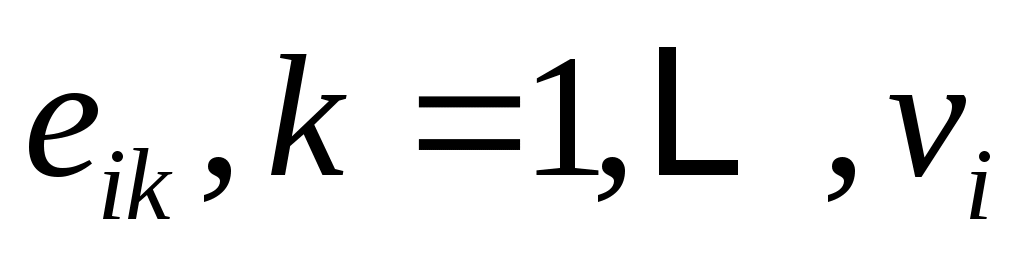 , являются независимыми линейными комбинациями векторов , являются независимыми линейными комбинациями векторов 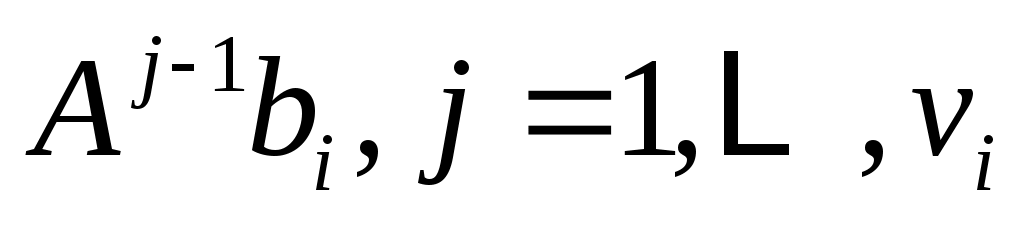 , и, следовательно, весь набор , и, следовательно, весь набор 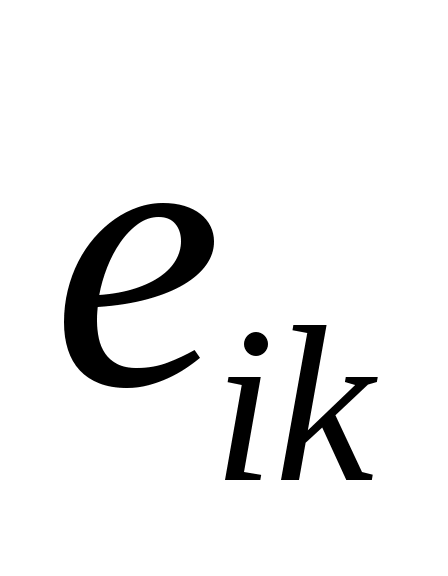 , является основой для , является основой для 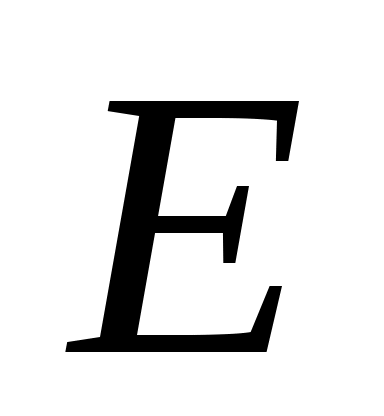 . Заметим, что для . Заметим, что для 
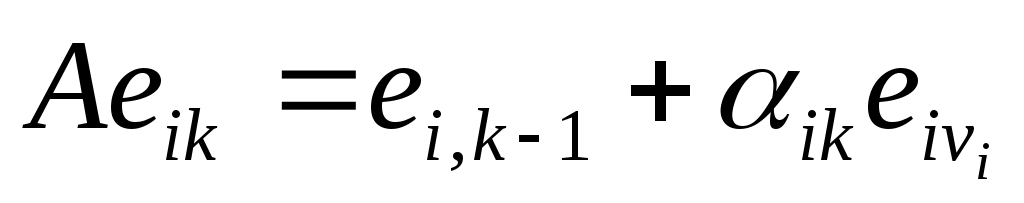 , , 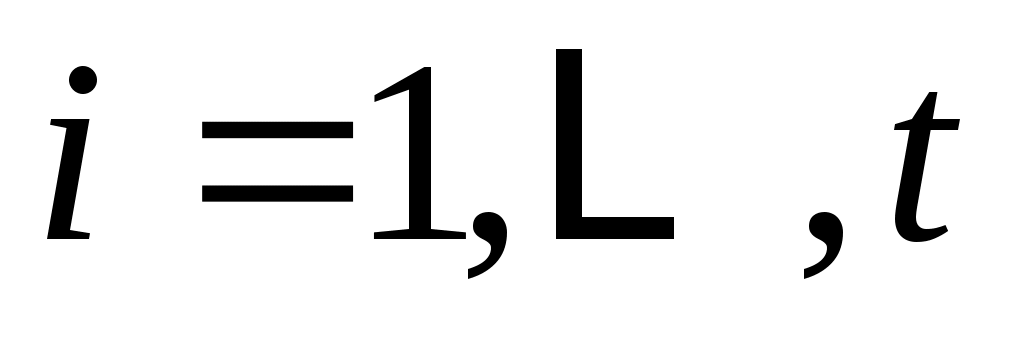 (9a) (9a)
Кроме того, из-за того факта, что относительное минимальный полином 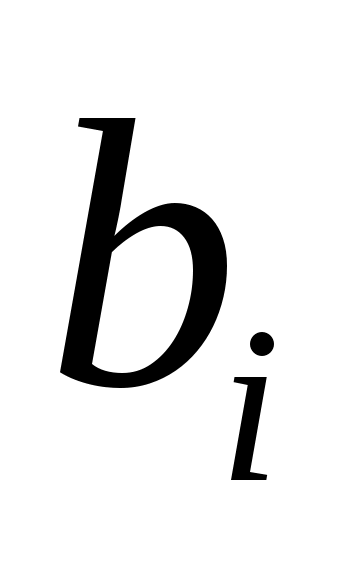  имеет степень имеет степень 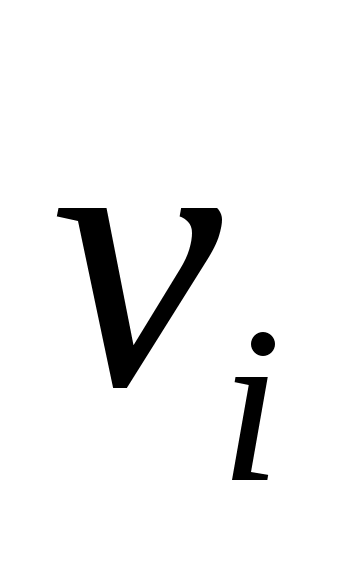 , следует (см. (7)) , следует (см. (7))
 , , 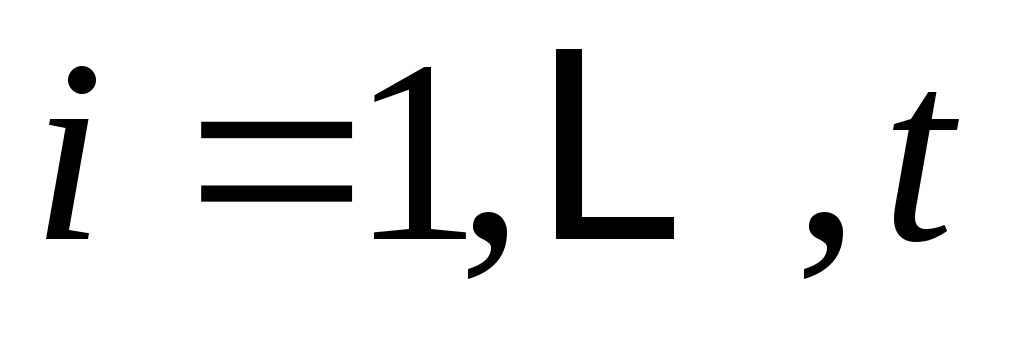 (9b) (9b)
для некоторых скаляров  , и где двойное суммирование не появляется, если , и где двойное суммирование не появляется, если 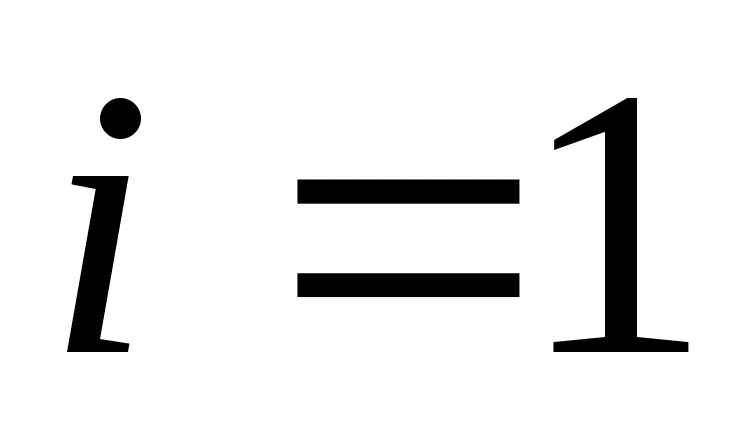 . .
Затем, используя (9), вычислите форму  , рассматриваемой как линейное преобразование в , рассматриваемой как линейное преобразование в 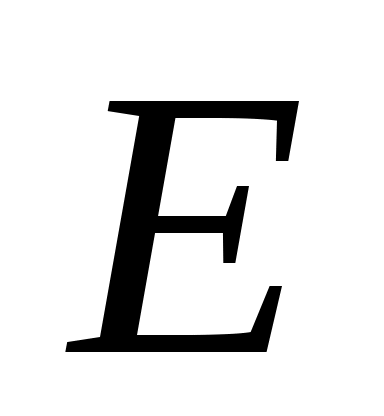 , относительно базиса , относительно базиса 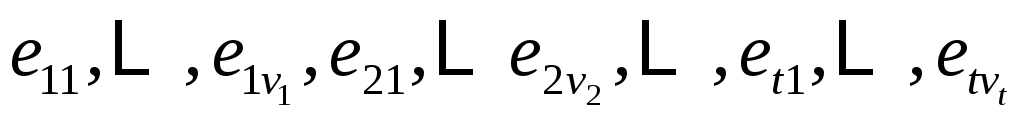 . То есть пусть . То есть пусть  будет матрицей с векторами столбцов будет матрицей с векторами столбцов 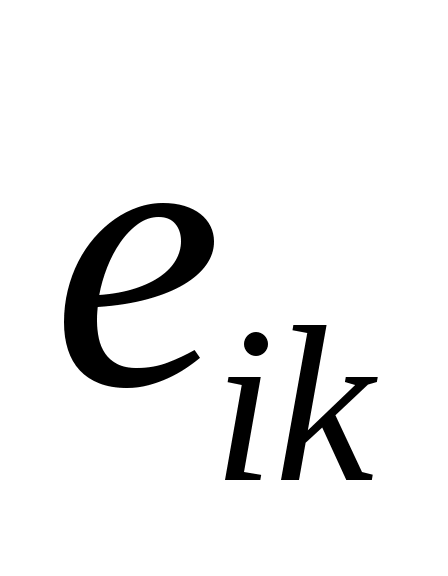 в только что написанном порядке, и пусть в только что написанном порядке, и пусть 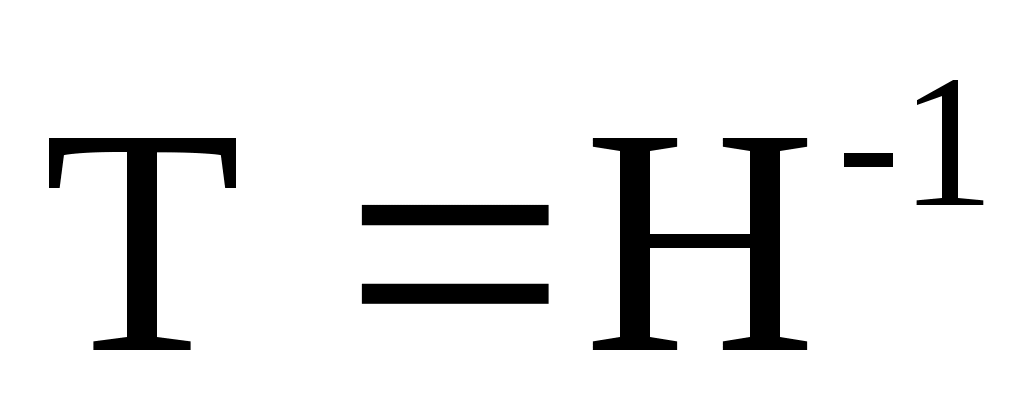 . Тогда . Тогда 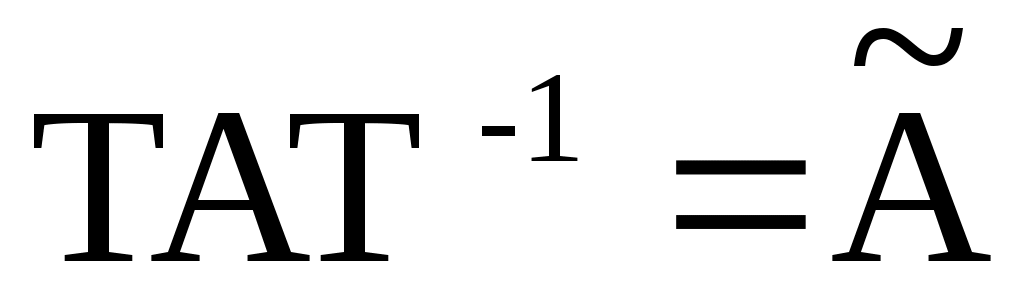 имеет блочную форму имеет блочную форму
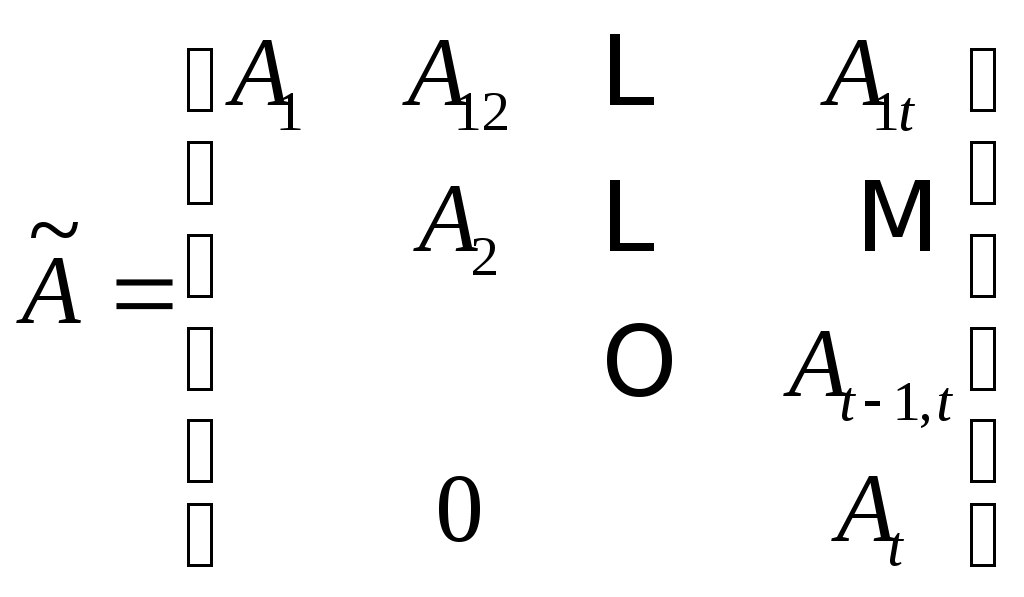 . (10) . (10)
В (10) матрицы  встречающиеся на диагонали встречающиеся на диагонали  являются сопутствующими матрицами являются сопутствующими матрицами 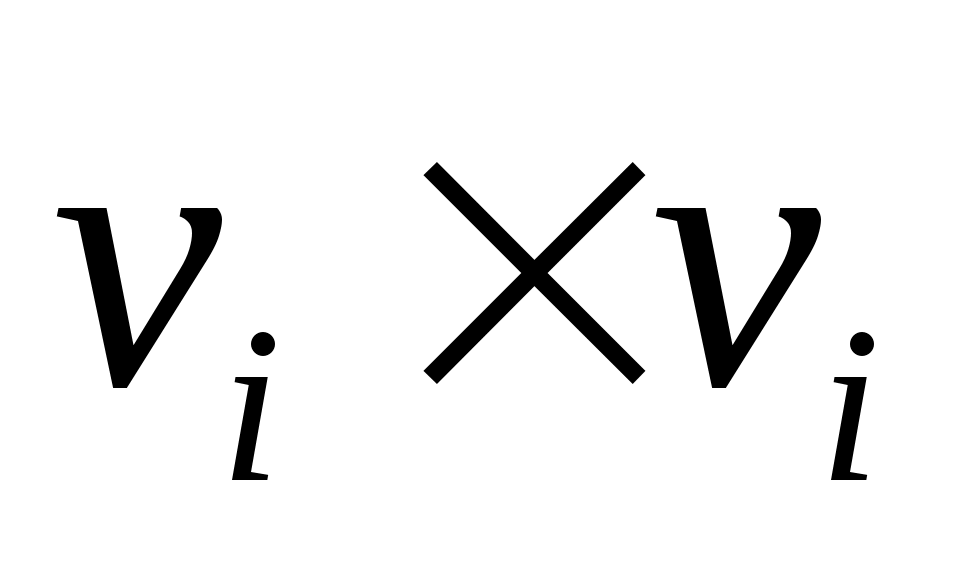 . .
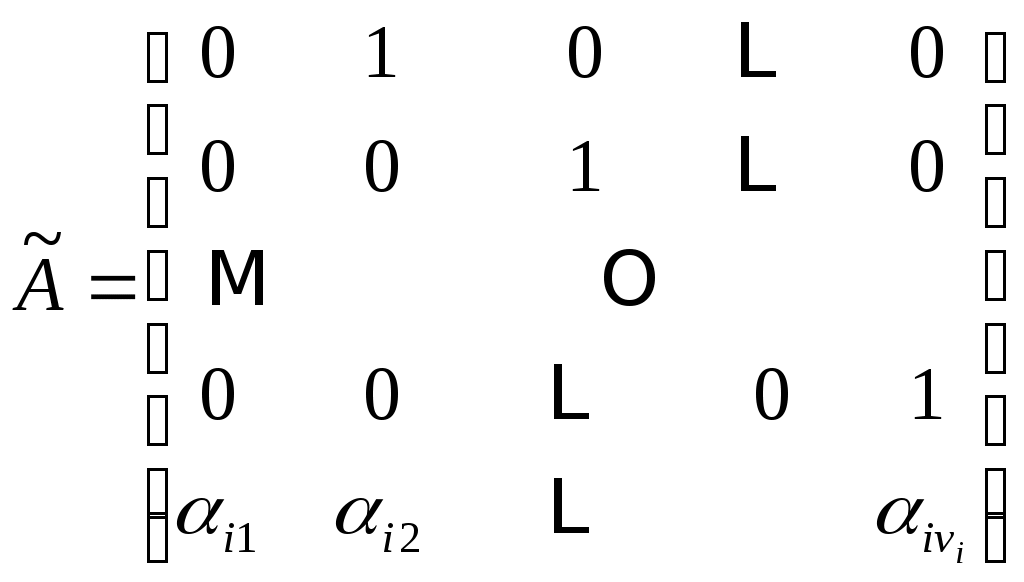 , , 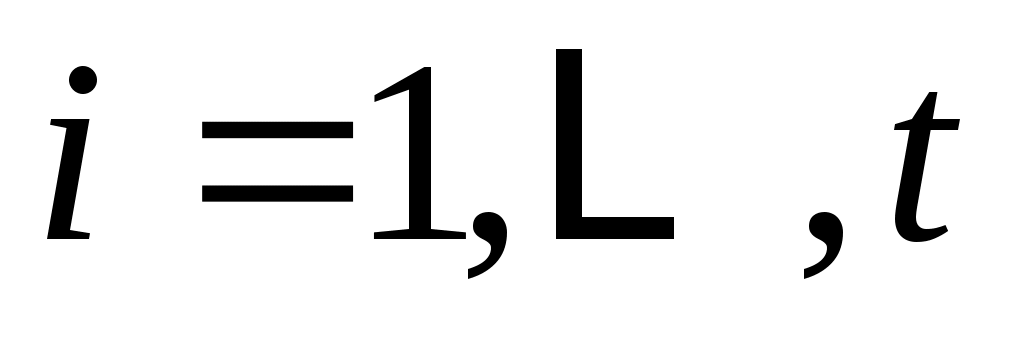 (11) (11)
и матрицы  имеют размерность имеют размерность 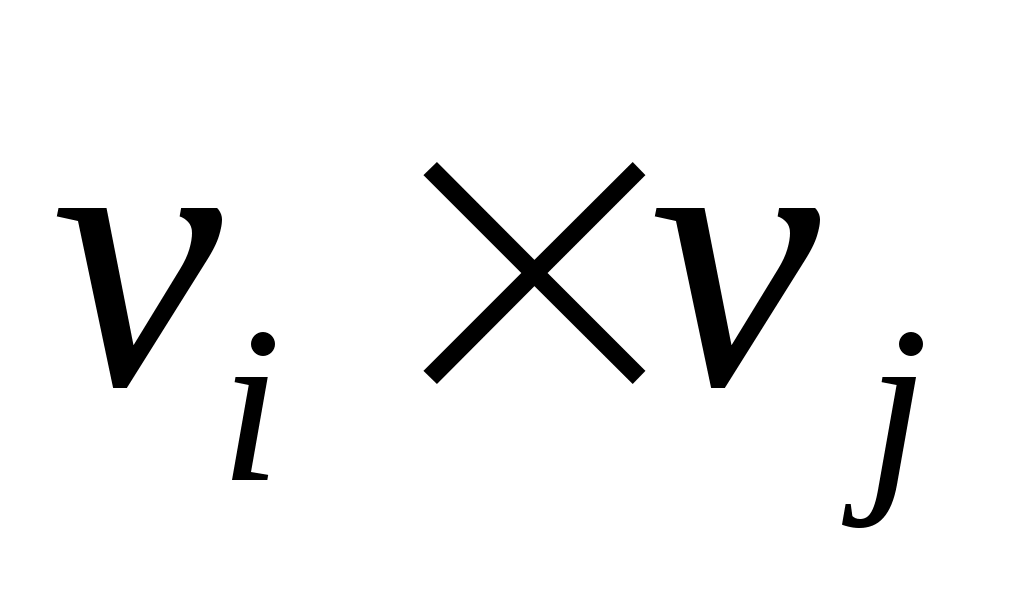 . .
Наконец, 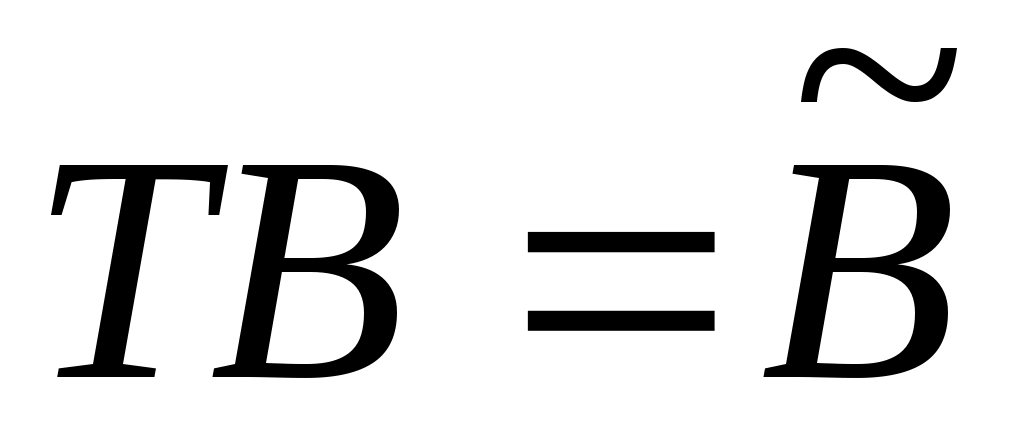 , где , где
 (12a) (12a)
здесь
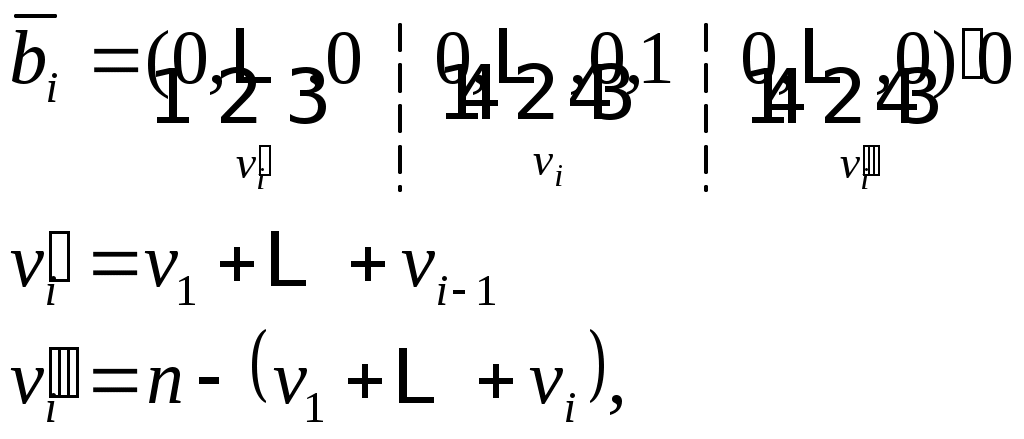 (12b) (12b)
и 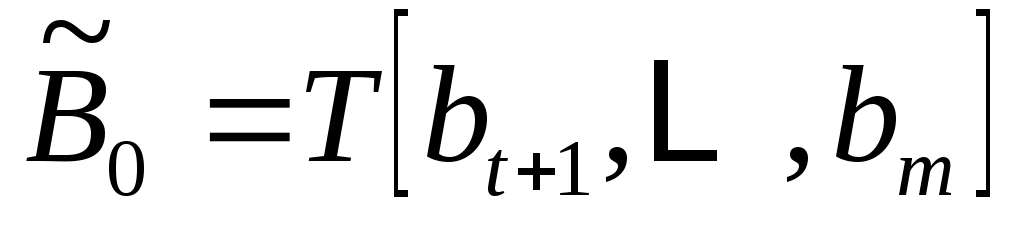 - матрица - матрица 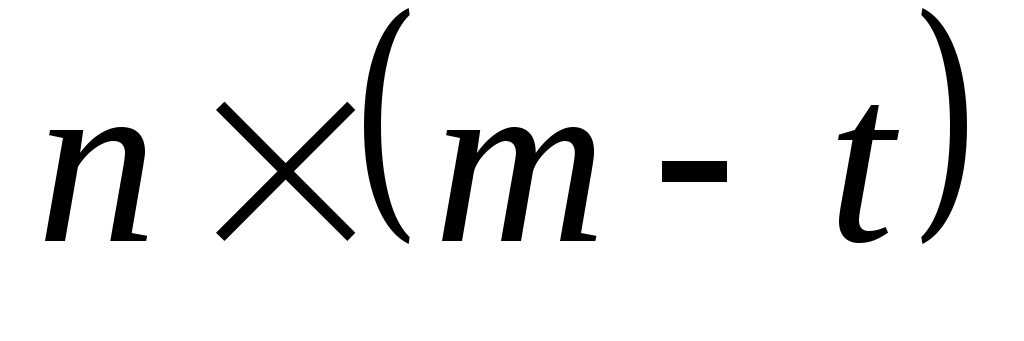 , которая не появляется, если , которая не появляется, если 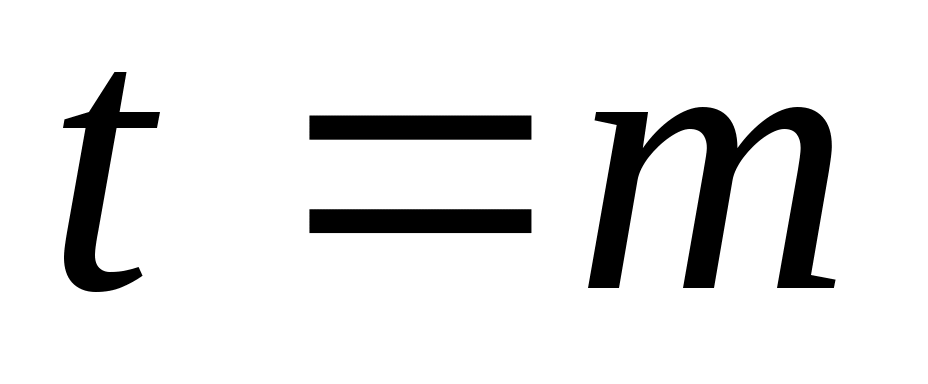 . .
Чтобы проверить детали (10), (ll) и (12), отметим, что 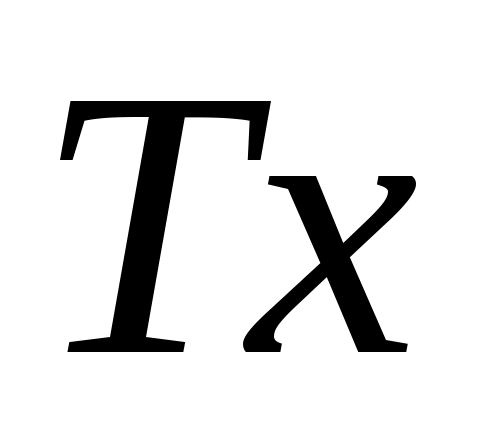 является столбцом компонентов является столбцом компонентов  в базисе в базисе 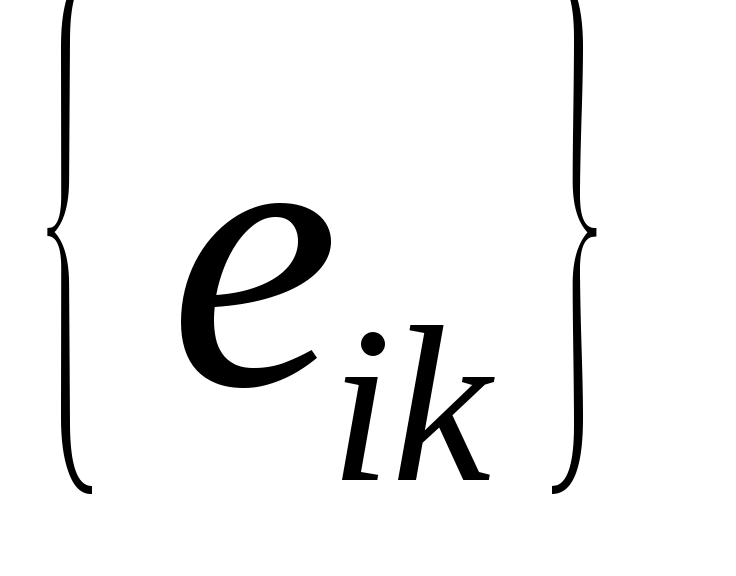 . .
Таким образом, 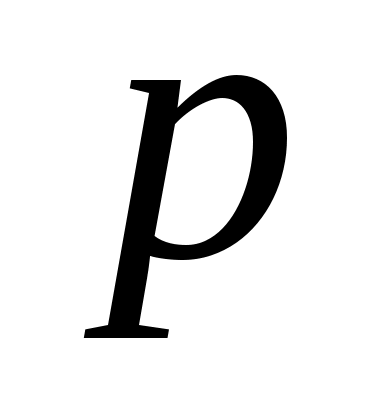 -й столбец -й столбец 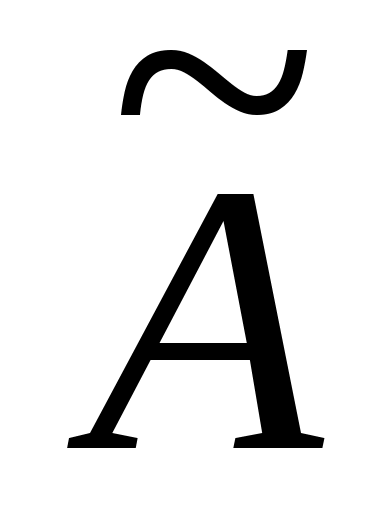 - это список компонентов, в этом базисе, - это список компонентов, в этом базисе, 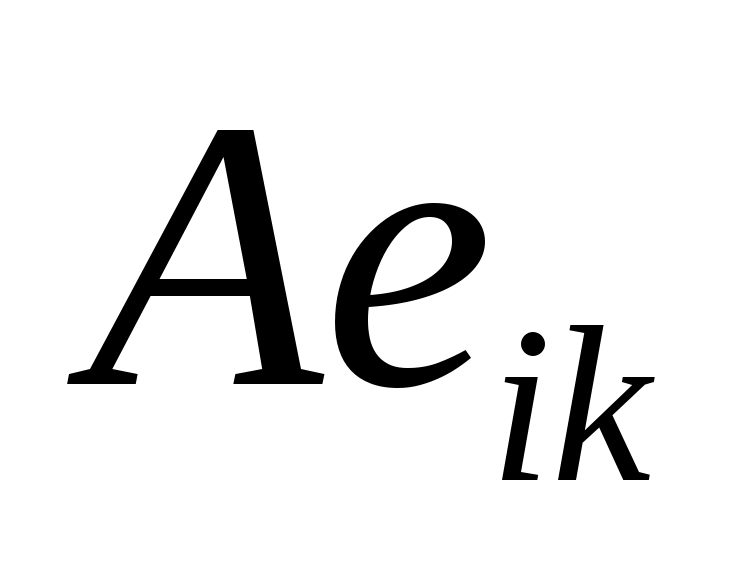 , где , где 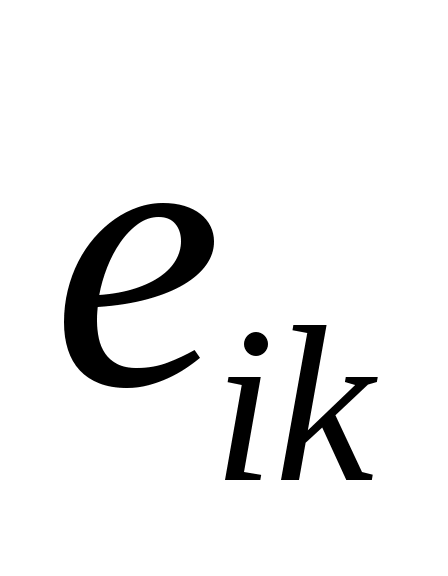 - это - это 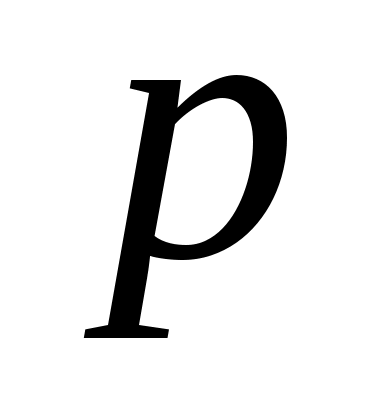 -й базисный вектор. Этот список можно прочитать из (9). Аналогично -й базисный вектор. Этот список можно прочитать из (9). Аналогично 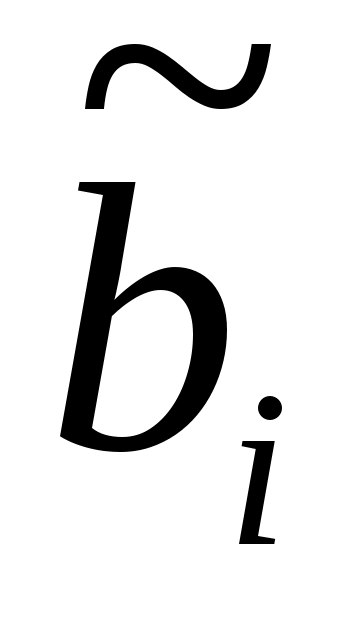 является столбцом компонент является столбцом компонент  , так что (12) сразу следует из (8b). , так что (12) сразу следует из (8b).
С 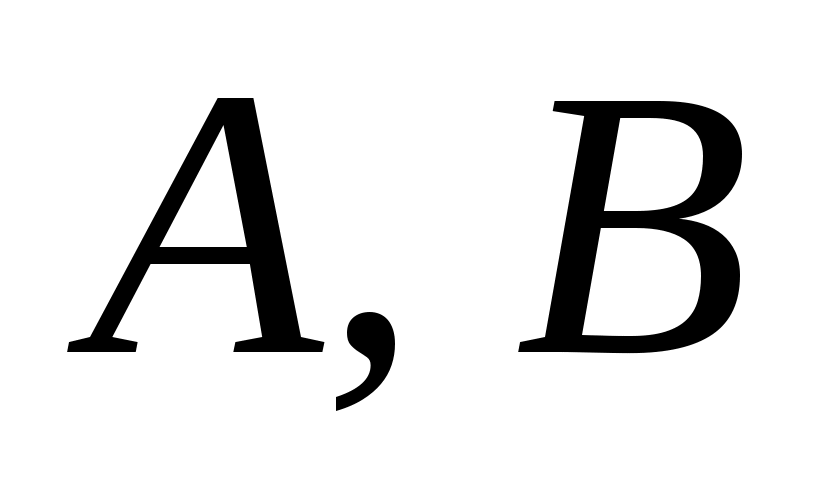 в канонической форме будет в конечном итоге показано, что собственные значения в канонической форме будет в конечном итоге показано, что собственные значения 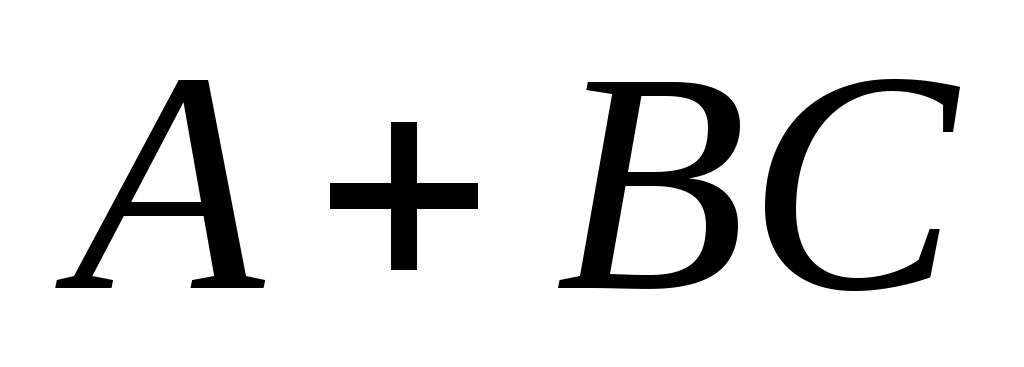 могут быть заданы произвольно. Положим могут быть заданы произвольно. Положим 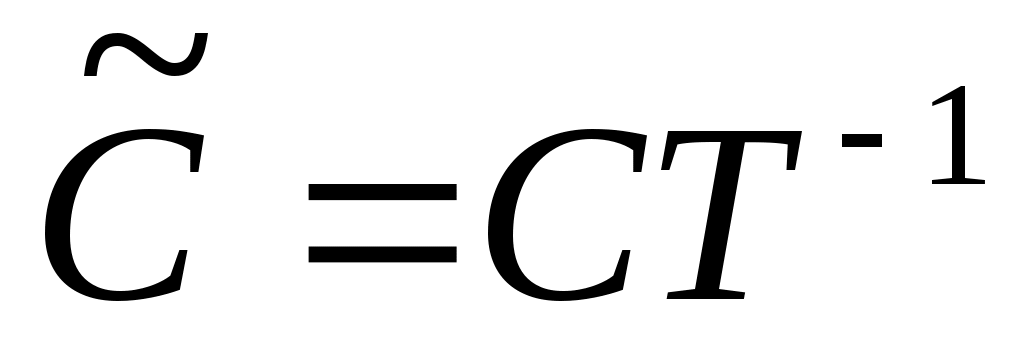 и наблюдаем, что матрица и наблюдаем, что матрица 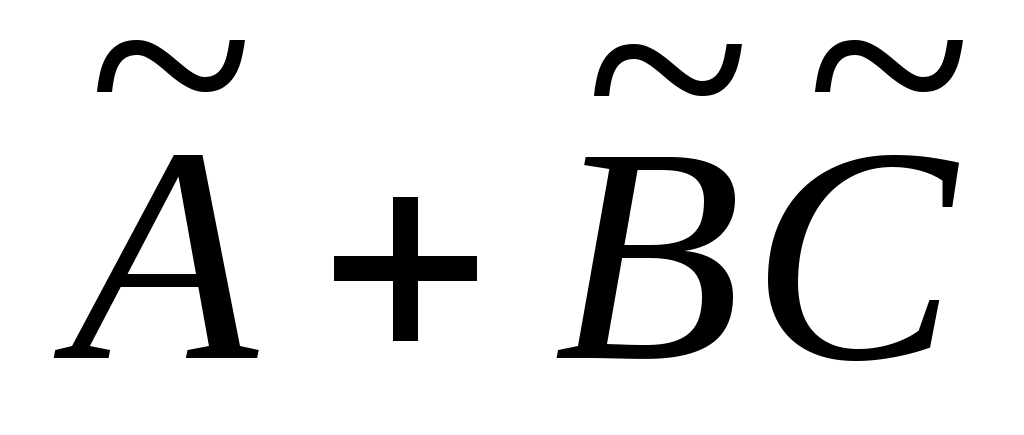 подобна под подобна под 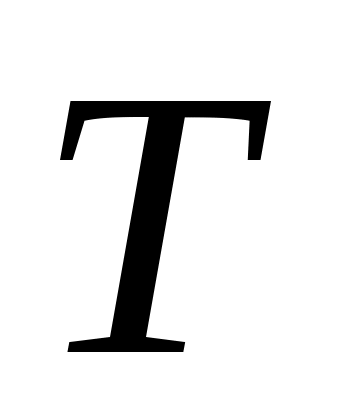 к к 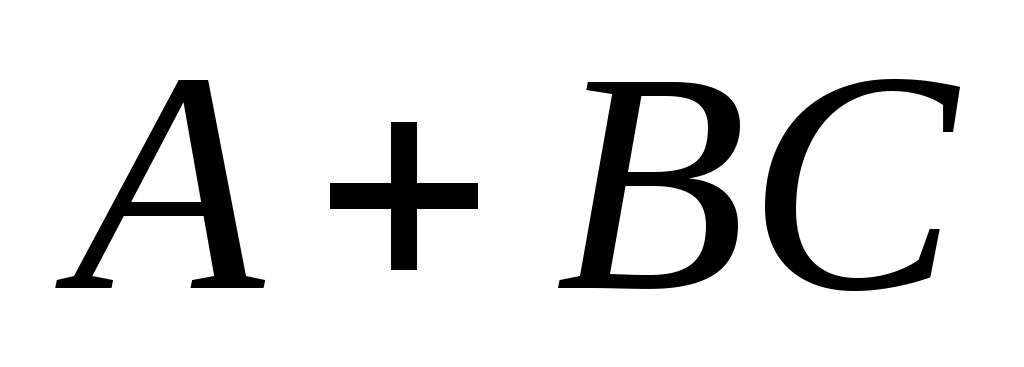 . Далее возьмите . Далее возьмите 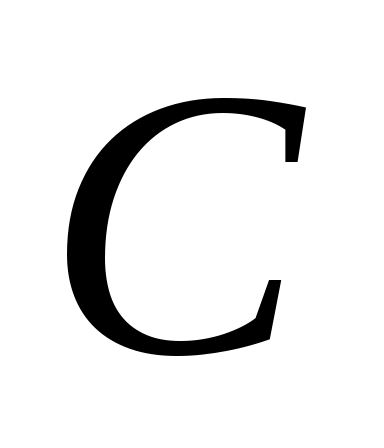 в виде в виде
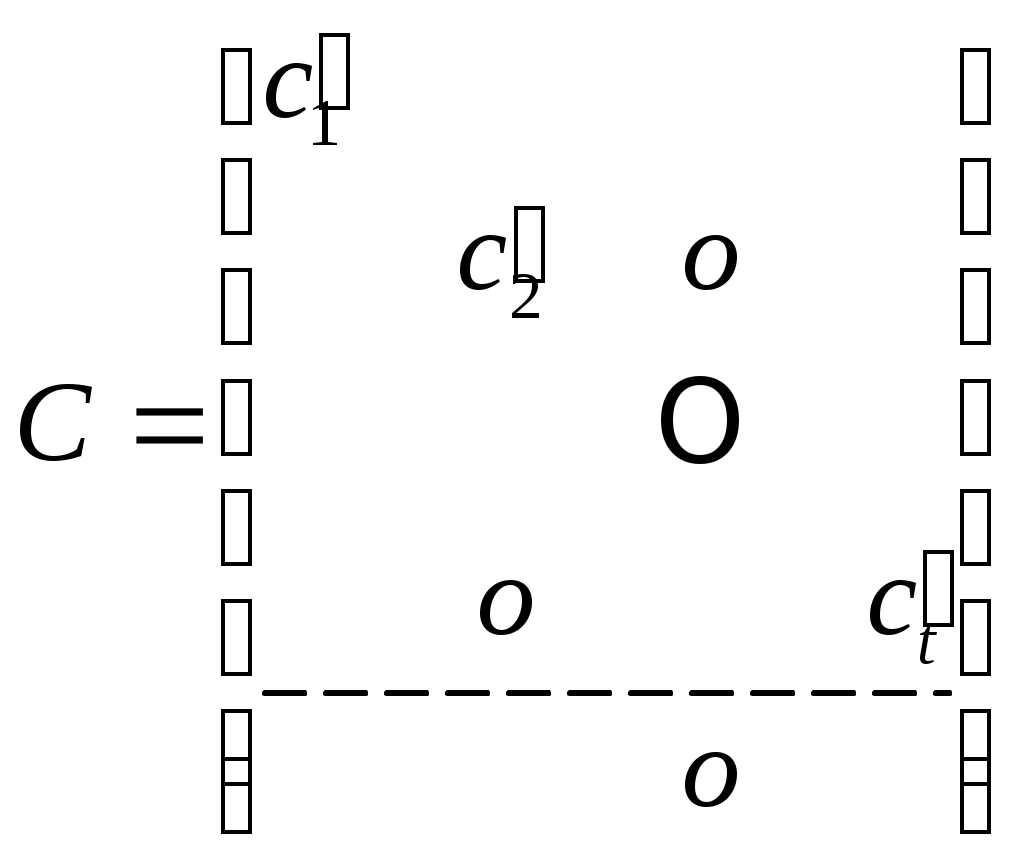 (13) (13)
где
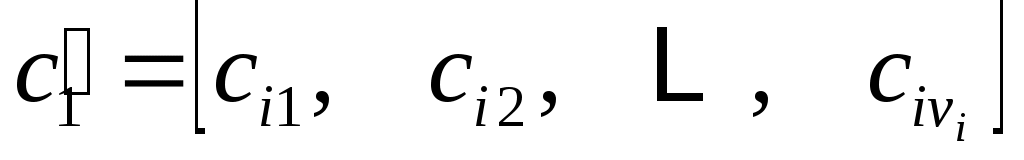 , , 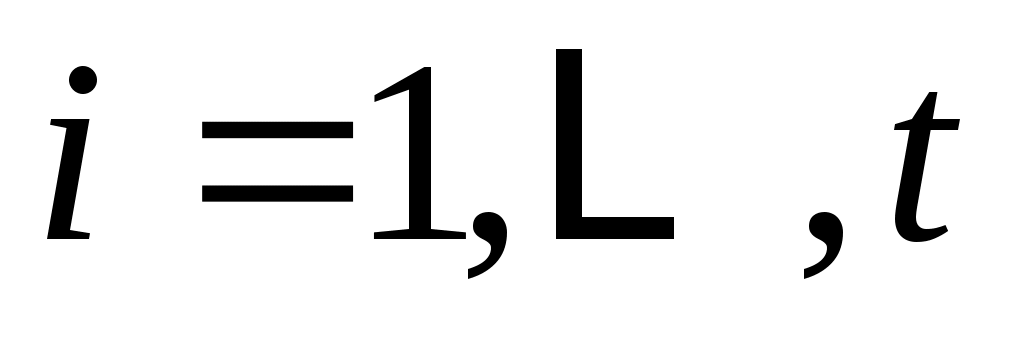 . .
В 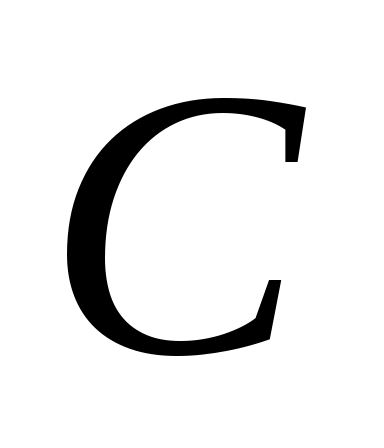 верхний блок имеет размерность верхний блок имеет размерность  , а нижний блок размера , а нижний блок размера 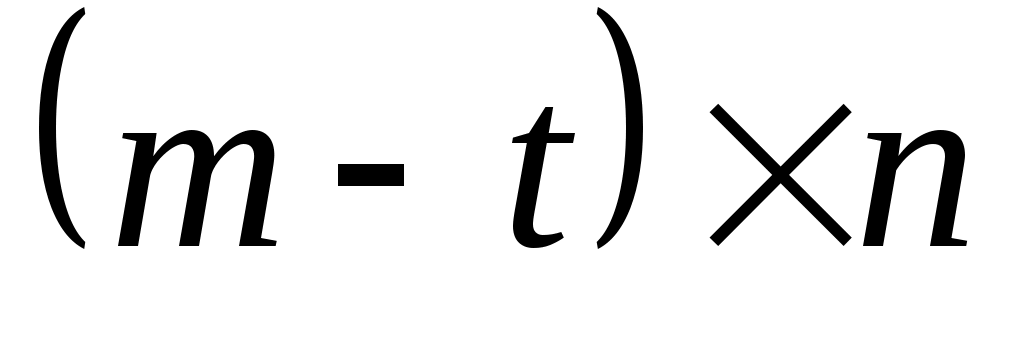 . Из (10)- (13) видно, что . Из (10)- (13) видно, что
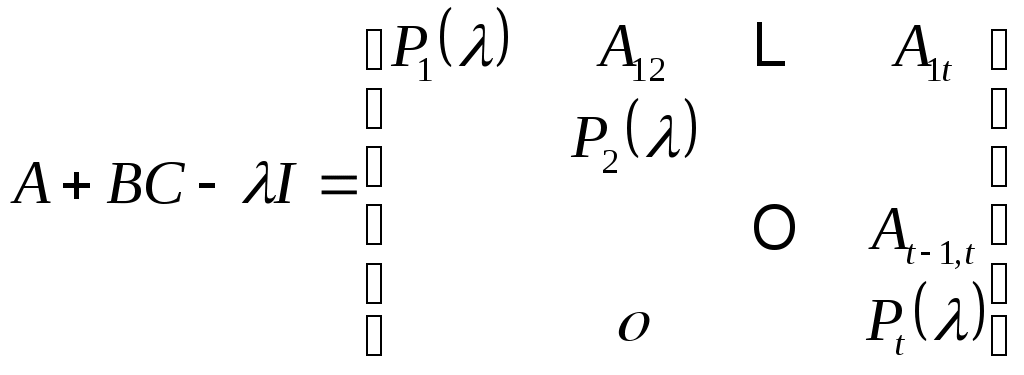
где, для 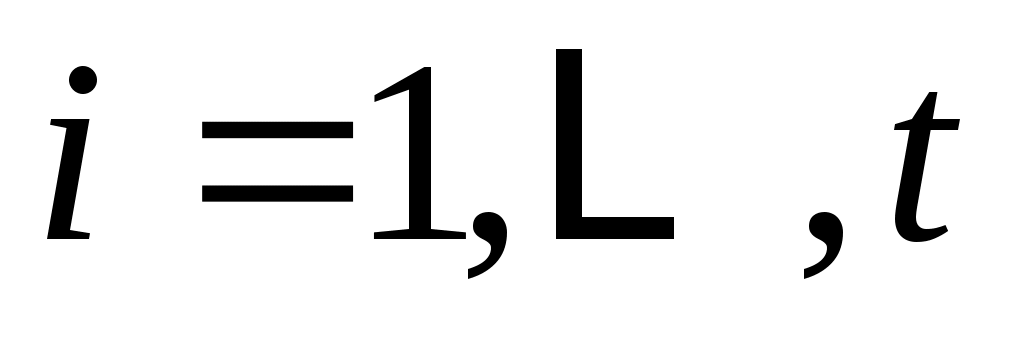 , ,
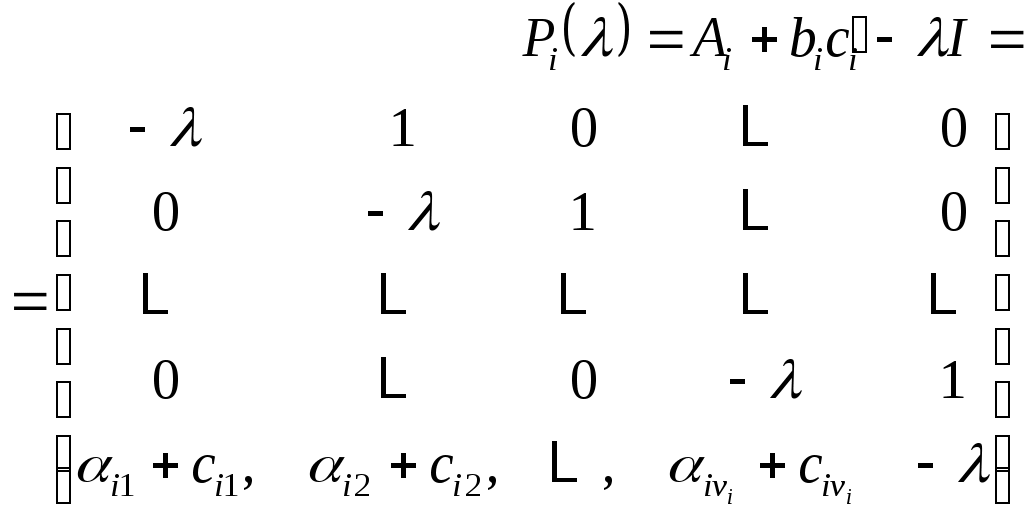 . .
Пусть 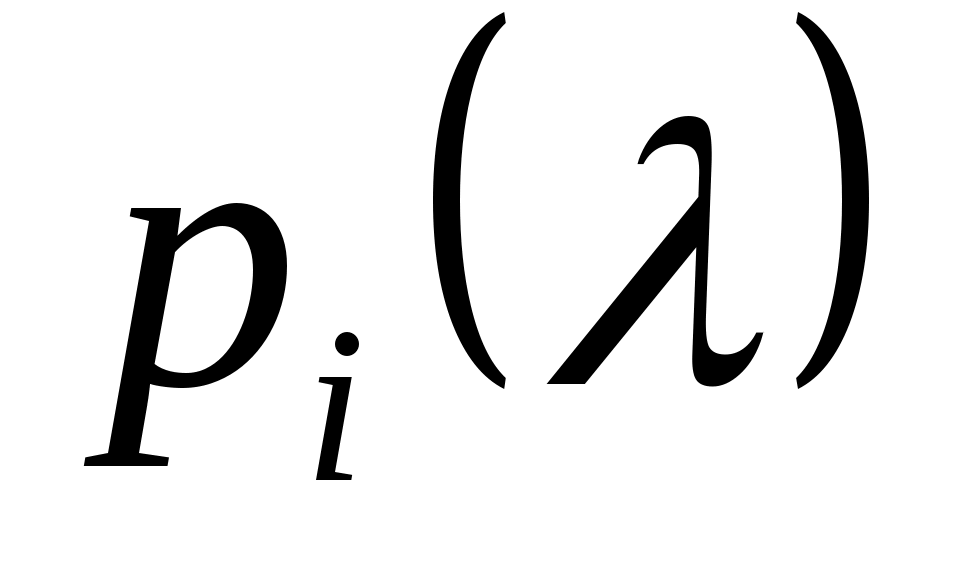 будет определителем будет определителем 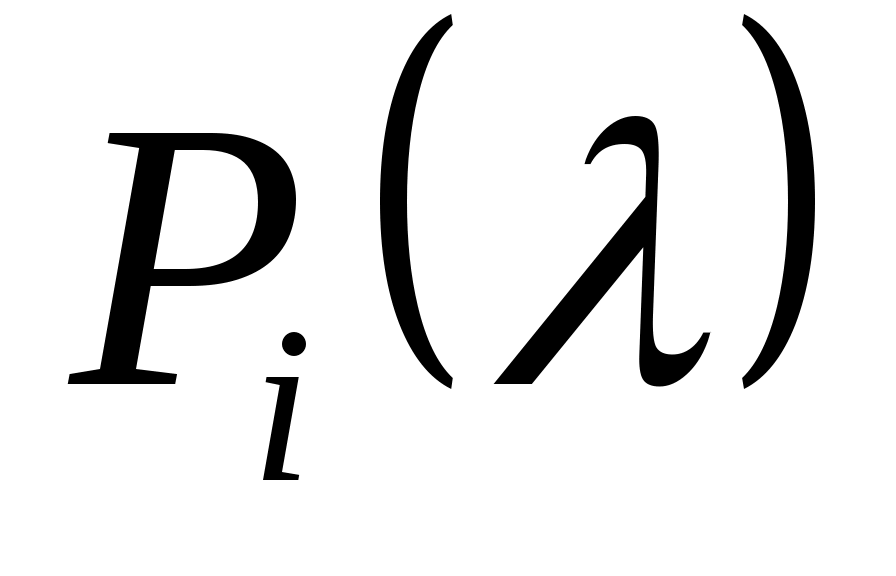 , то есть , то есть
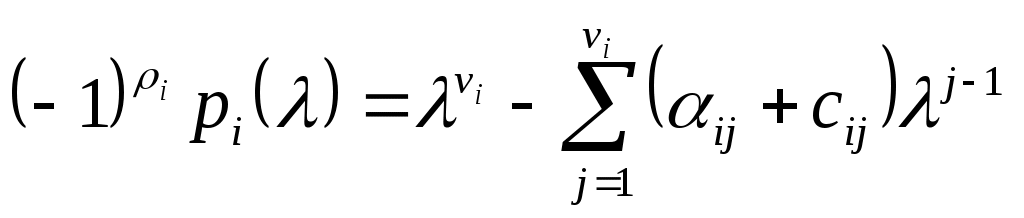 . (14) . (14)
Из треугольной формы 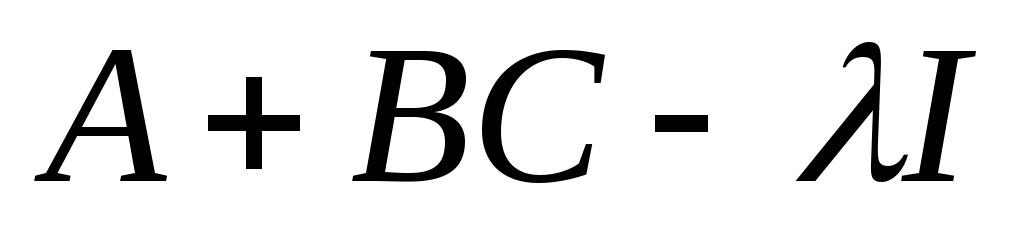 следует, что следует, что
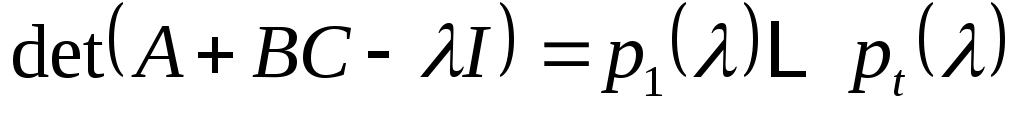 . .
Также из (14) ясно, что нули числа 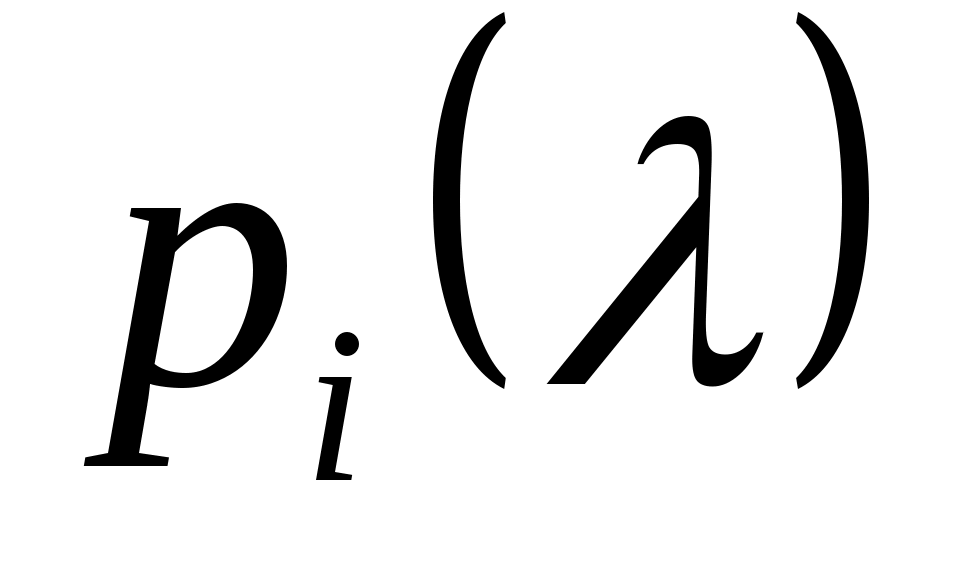 могут быть назначены произвольно (при условии сопряженности комплексных нулей) путем правильного выбора действительных коэффициентов могут быть назначены произвольно (при условии сопряженности комплексных нулей) путем правильного выбора действительных коэффициентов  . Это показывает, что, в частности, система (1) всегда может быть стабилизирована путем соответствующего выбора . Это показывает, что, в частности, система (1) всегда может быть стабилизирована путем соответствующего выбора 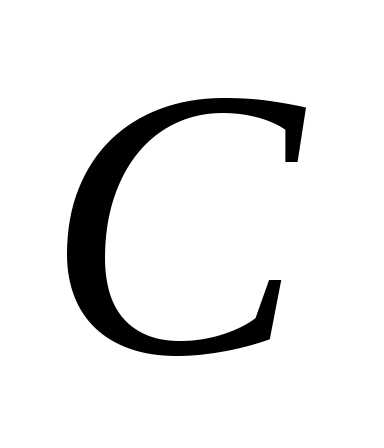 . .
Чтобы показать, что может быть назначен произвольный набор собственных значений  , необходимо учитывать тот факт, что матрицы , необходимо учитывать тот факт, что матрицы 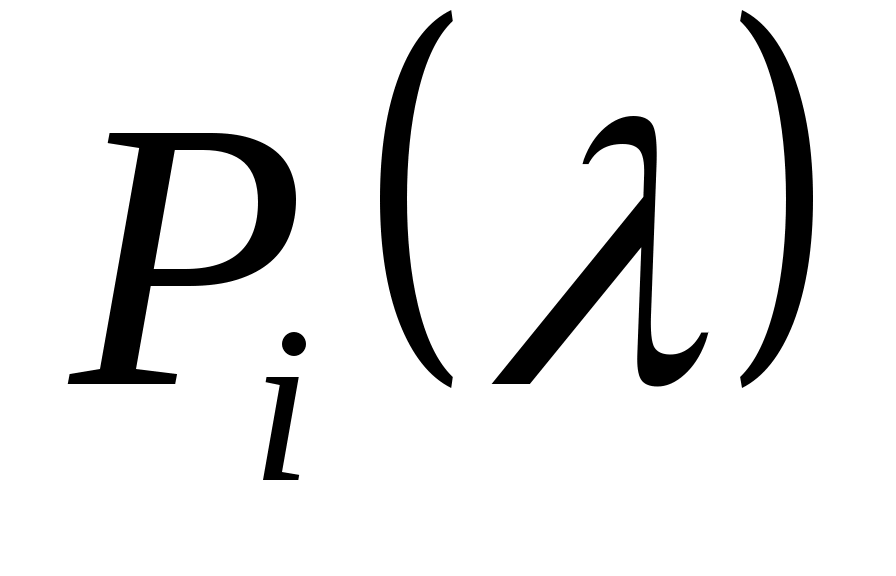 имеют фиксированную размерность. Если, например, имеют фиксированную размерность. Если, например, 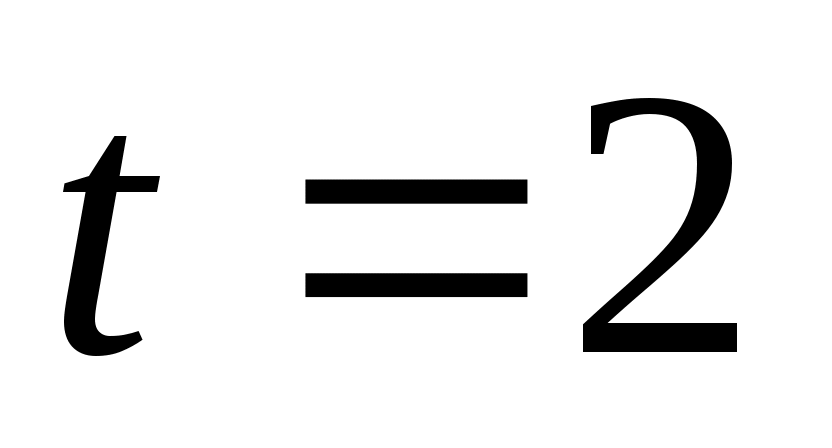 и и  каждый имеют размерность каждый имеют размерность 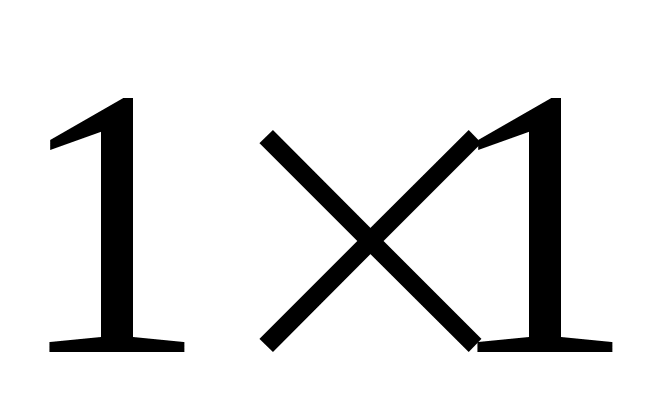 , невозможно назначить произвольную комплексную пару собственных значений путем независимой регулировки , невозможно назначить произвольную комплексную пару собственных значений путем независимой регулировки  . Это дополнительная сложность, связанная с ограничением реальных параметров. Для продолжения пусть . Это дополнительная сложность, связанная с ограничением реальных параметров. Для продолжения пусть 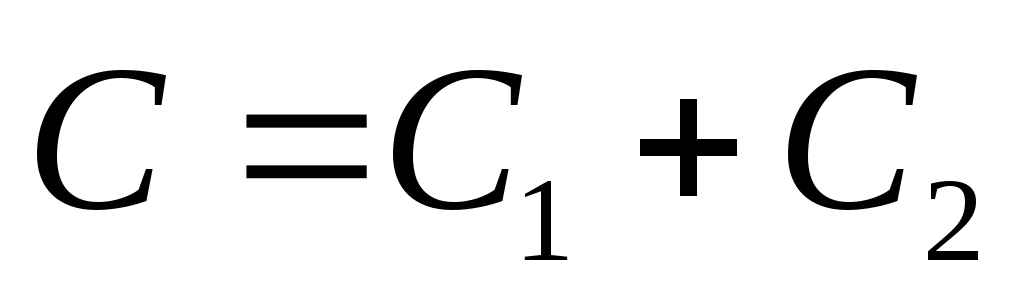 , где , где  имеет вид (13) и подчиняется только требованию, чтобы все собственные значения имеет вид (13) и подчиняется только требованию, чтобы все собственные значения 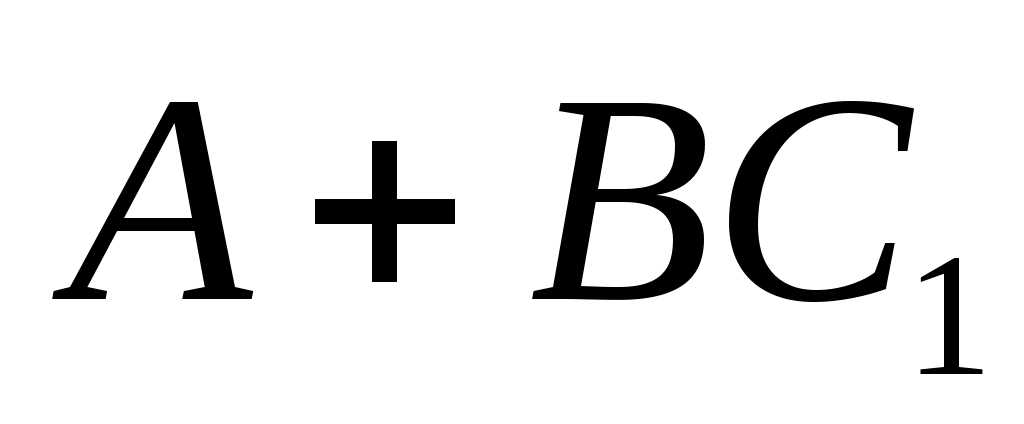 были различны. Только что было замечено, что такой выбор были различны. Только что было замечено, что такой выбор  возможен. Тогда по лемме 1 пространство возможен. Тогда по лемме 1 пространство 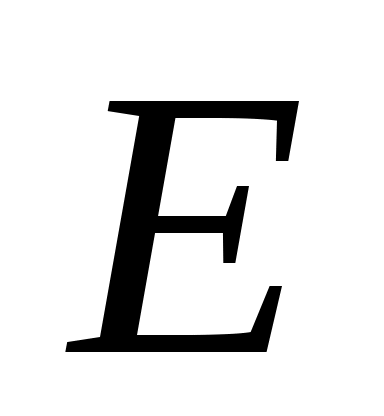 циклически относительно матрицы циклически относительно матрицы 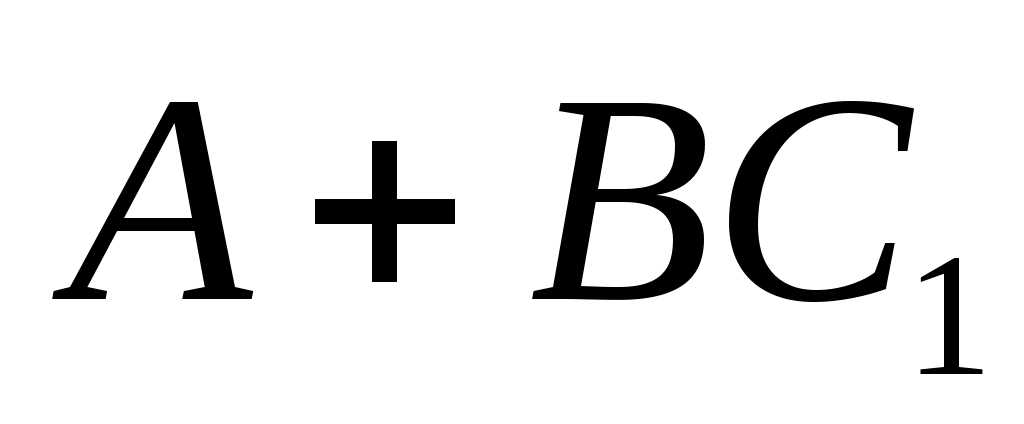 . По лемме 4 . По лемме 4 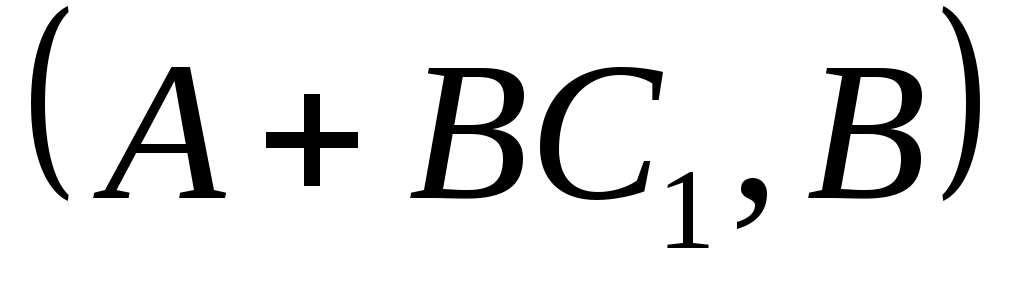 является управляемым. Применяя лемму 3, можно найти является управляемым. Применяя лемму 3, можно найти 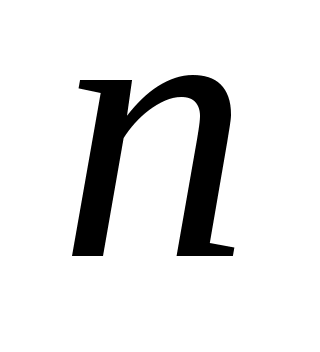 -вектор -вектор 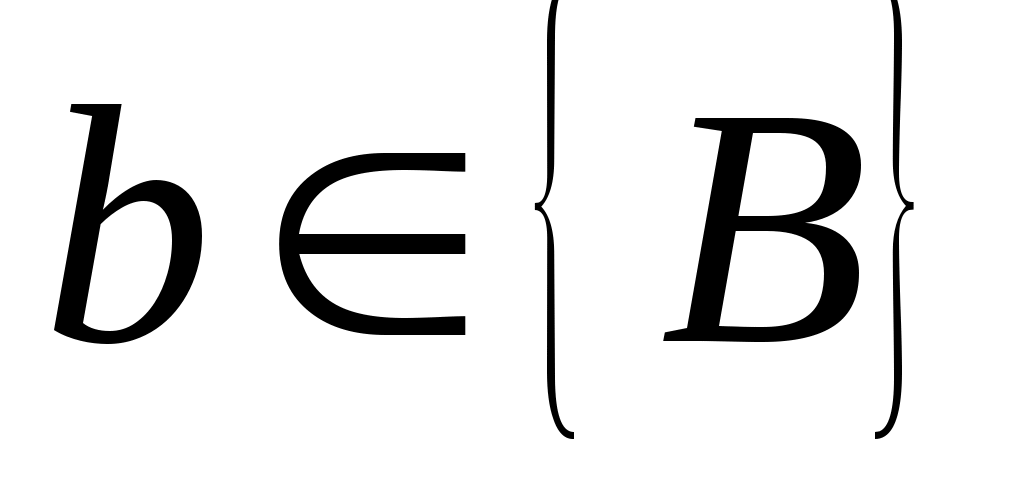 такой, что такой, что 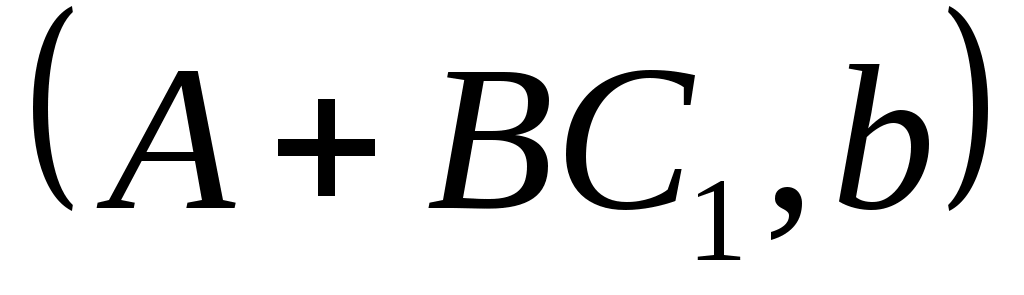 является управляемым. Теперь является управляемым. Теперь 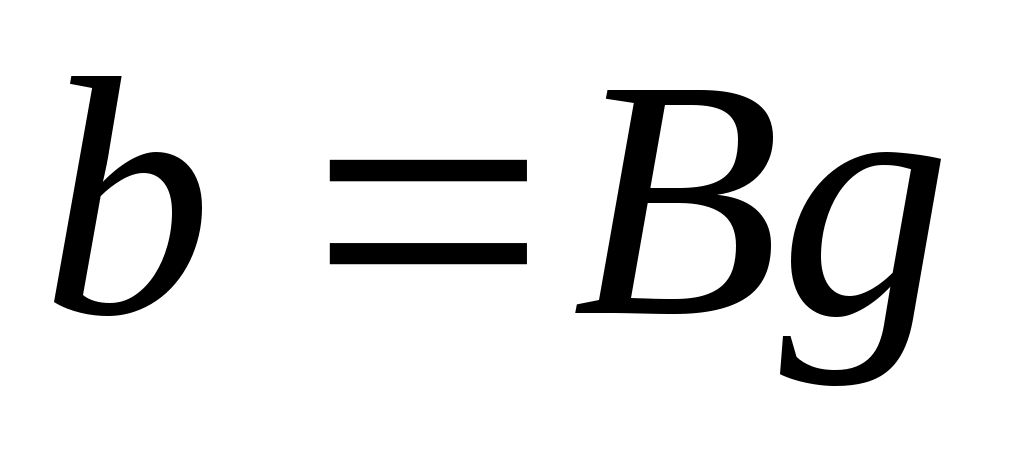 для подходящей для подходящей 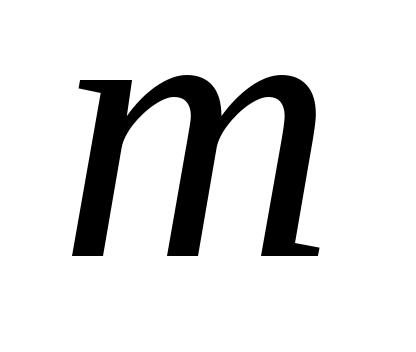 вектор вектор 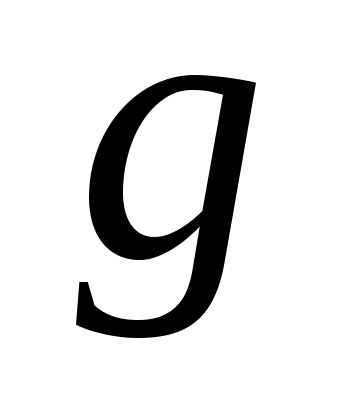 . Таким образом, если . Таким образом, если  принимается в виде принимается в виде
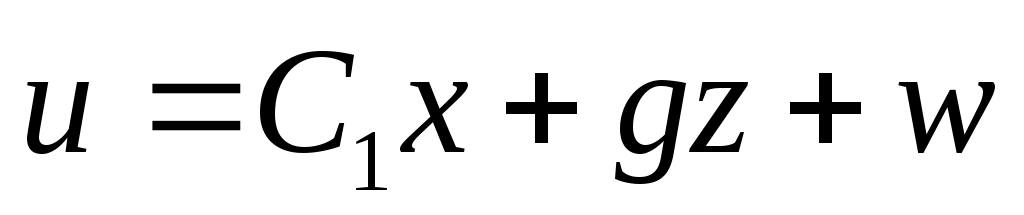
с  скаляром и вектором скаляром и вектором 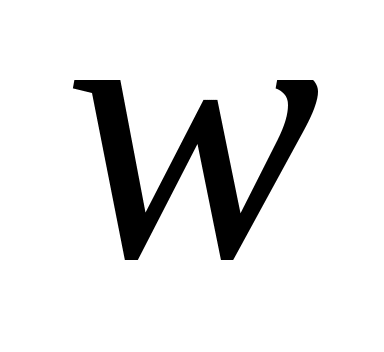 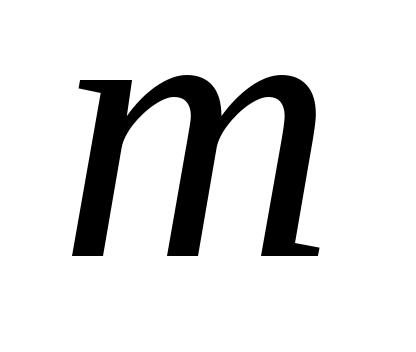 , то система (1) становится , то система (1) становится
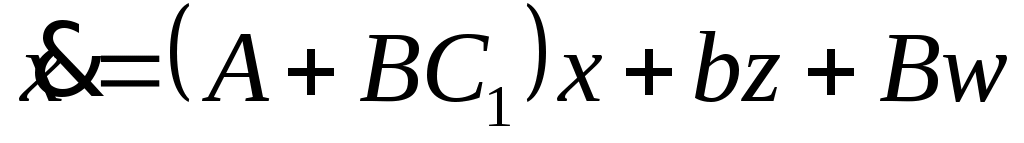 . .
Наконец, поскольку теорема верна в случае с одним входом,  можно выбрать в виде можно выбрать в виде

таким образом, что матрица 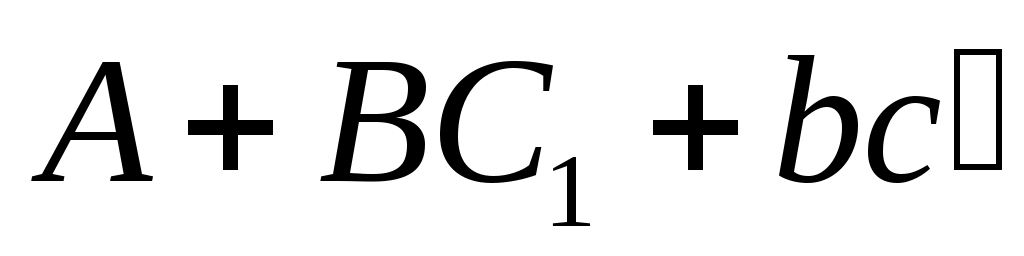 имеет требуемый набор собственных значений имеет требуемый набор собственных значений  . То есть матрица «усиления» . То есть матрица «усиления»
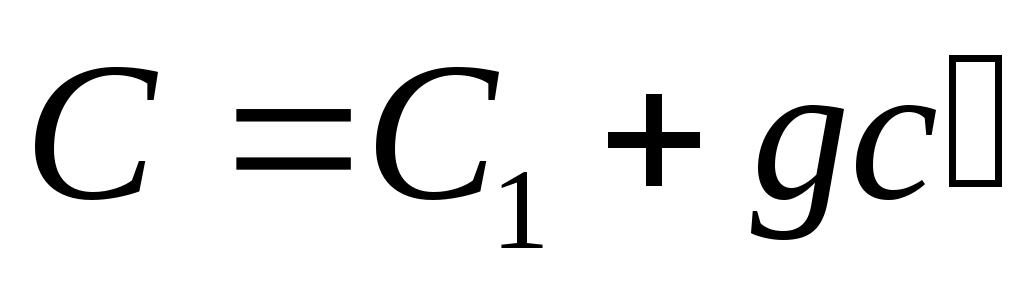
имеет обязательное свойство. Теорема доказана.
|
 Скачать 0.91 Mb.
Скачать 0.91 Mb.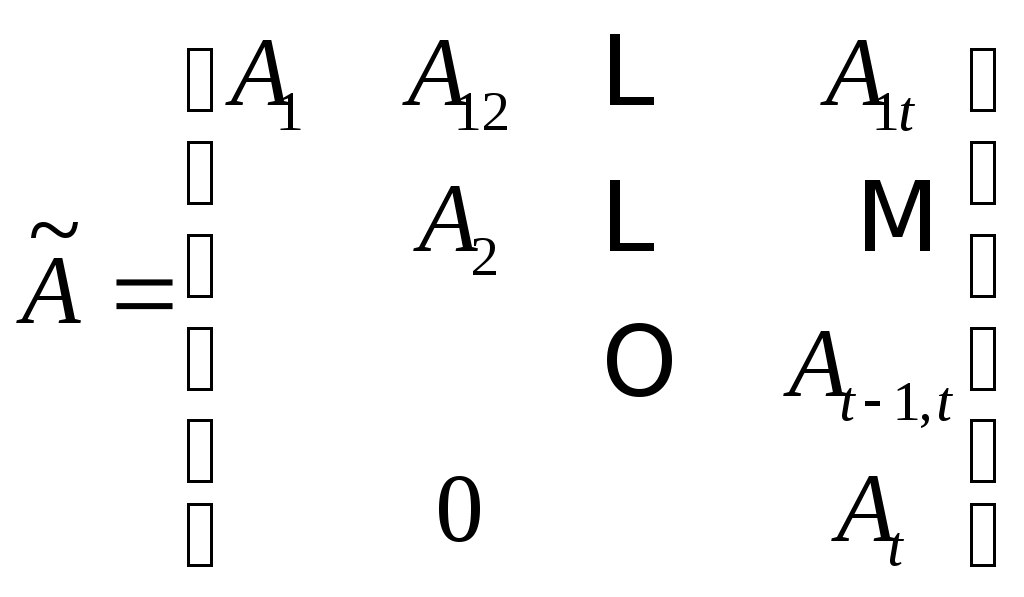 . (10)
. (10)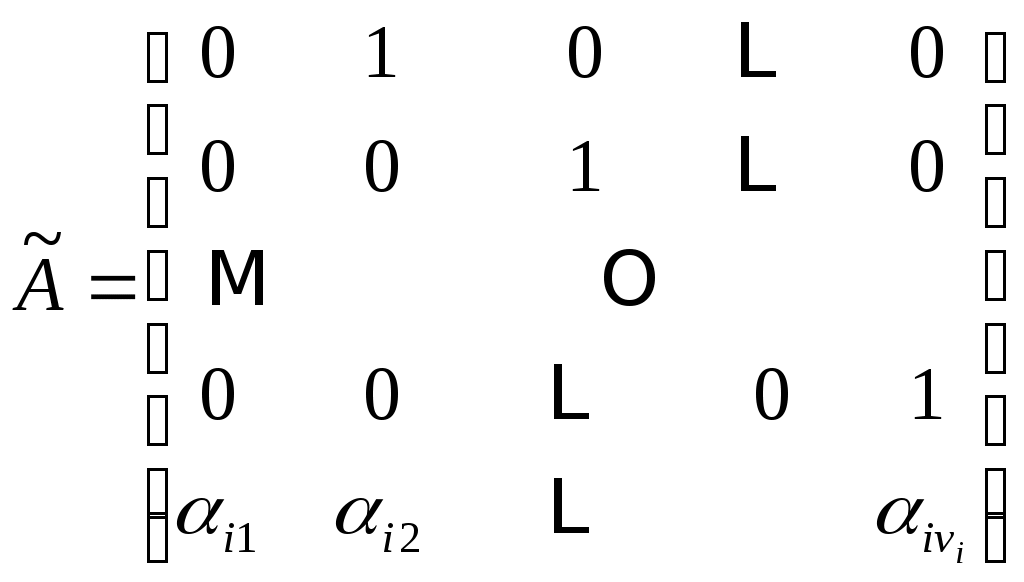 ,
, 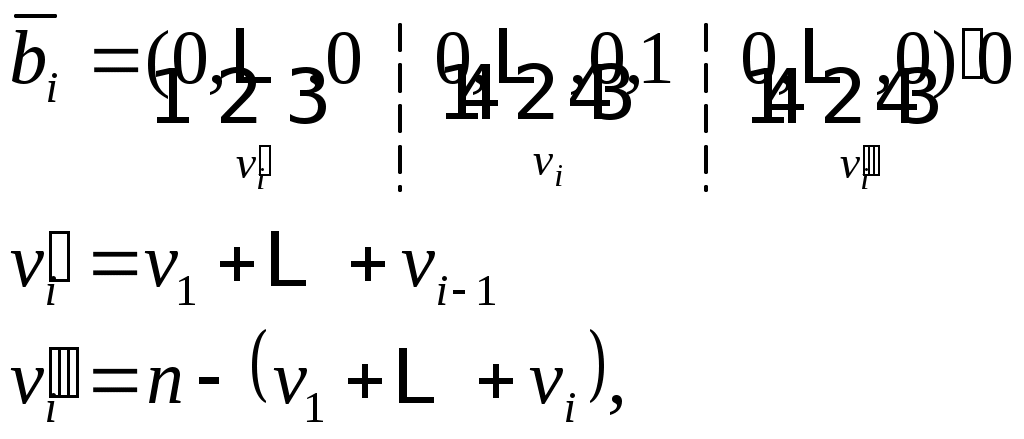 (12b)
(12b)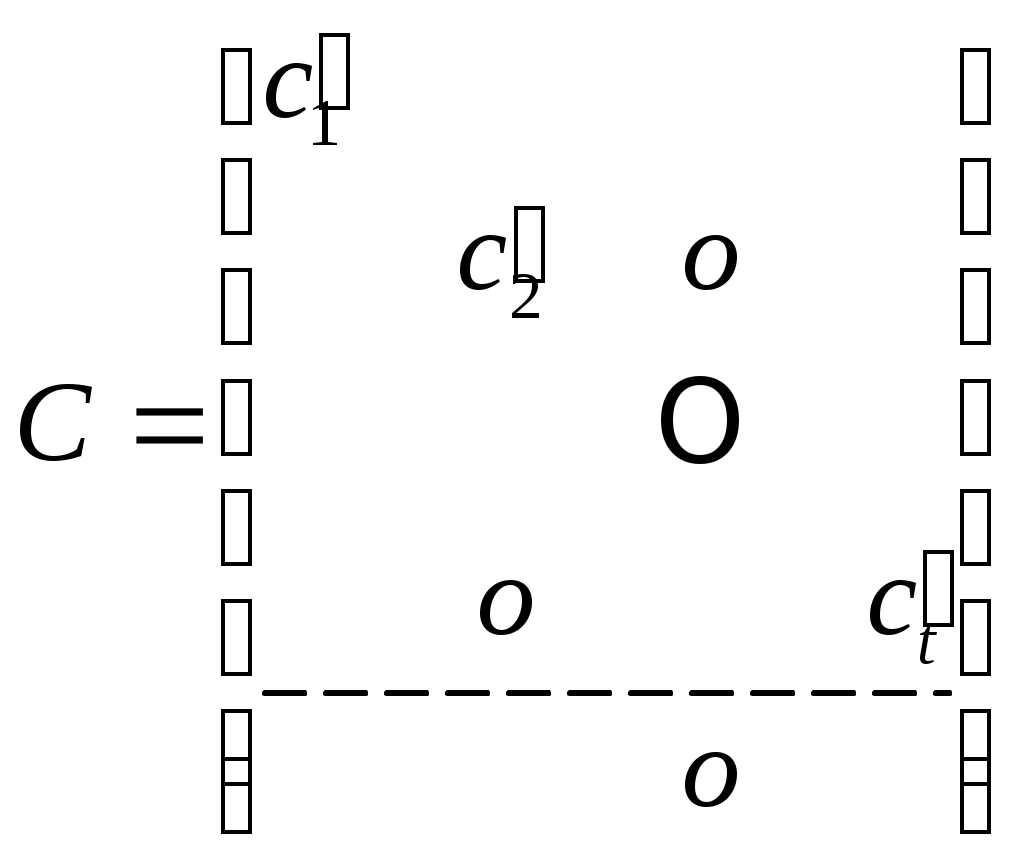 (13)
(13)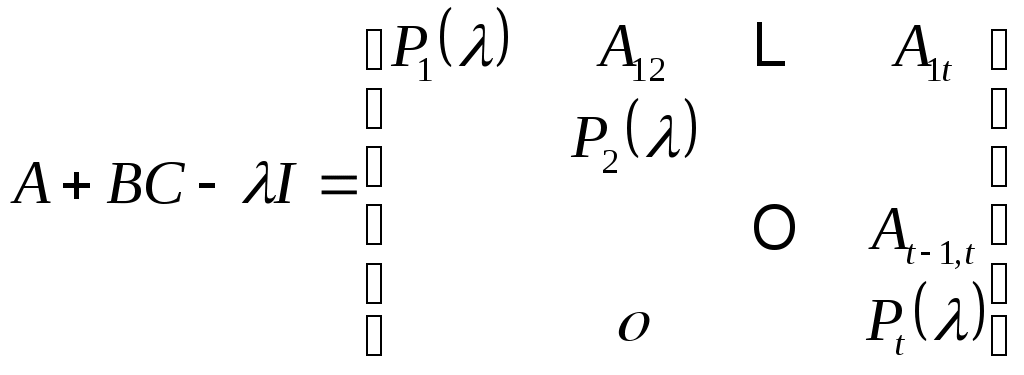
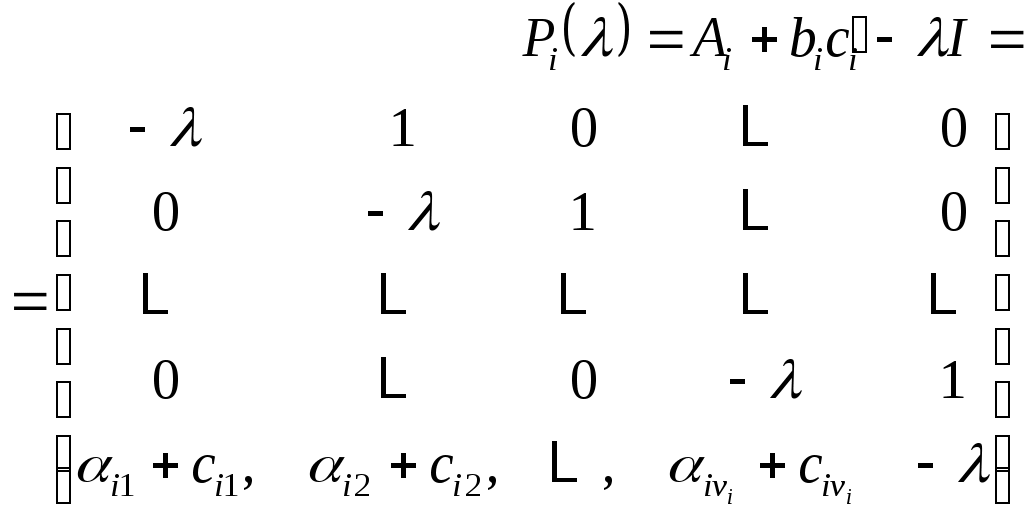 .
.