О НАЗНАЧЕНИИ ПОЛЮСОВ В МНОГОВХОДНЫХ УПРАВЛЯЕМЫХ ЛИНЕЙНЫХ СИСТЕМА. О назначении полюсов в многовходных управляемых линейных системах

• Название: О назначении полюсов в многовходных управляемых линейных системах
• Дата: 06.02.2023
• Размер: 0.91 Mb.
• Имя файла: О НАЗНАЧЕНИИ ПОЛЮСОВ В МНОГОВХОДНЫХ УПРАВЛЯЕМЫХ ЛИНЕЙНЫХ СИСТЕМА.doc
• Тип: Документы; #922099
• страница: 3 из 3

Комментарии

1) Конструкцию в доказательстве необходимости можно суммировать в терминах блок-схемы (рис.1). После выбора подходящего набора переменных состояния (каноническая форма (8) - (12)) конструктор строит внутренний цикл обратной связи (через матрицу 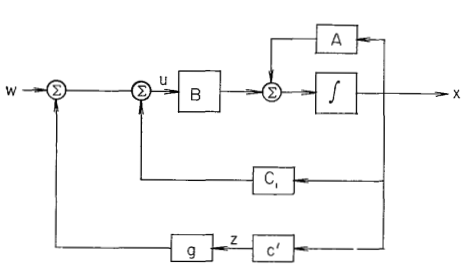), который делает систему циклической, то есть управляемой одним входом. Затем разработчик выбирает подходящий ввод в виде ( -генератор ) и завершает внешний цикл, устанавливая для достижения требуемого размещения полюсов.



Рисунок 1. Построение в доказательстве после выбора канонических переменных состояния.
2) На практике может быть много способов выбора переменных состояния и величин , , для достижения заданного назначения полюсов. Использование этой свободы с помощью подходящих критериев проектирования является интересной проблемой современных исследований [5].

3) Стоит отметить, что для данной пары может существовать более одной «канонической» формы (10)-(12). То есть матрица в (10) может не раскрывать внутреннюю структуру , как это делают обычные рациональные канонические разложения в блочно-диагональные формы [3]. Недостаток таких блочно-диагональных представлений состоит в том, что, как правило, циклические подпространства, соответствующие отдельным блокам, не обязательно должны иметь образующие в подпространстве . Если они это делают, соответствующие элементы управления полностью не взаимодействуют.

Применение к стабилизации. Ссылаясь на (2), естественно сказать, что пара стабилизируема, если существует матрица такая, что матрица стабильна, то есть все ее собственные значения имеют отрицательные вещественные части. Очевидно, что если управляемо, то стабилизируемо. Будет показано, что стабилизируемость эквивалентна более слабому свойству, что, по крайней мере, «неустойчивые моды» являются управляемыми.

Чтобы быть точным, пусть минимальный полином для относительно будет учтено как



где все нули лежат в замкнутой правой части комплексной плоскости, а все нули лежат в открытой левой полуплоскости. Определить подпространство неустойчивых мод



и пусть обозначает матрицу управляемости (см. Введение).

ПРЕДЛОЖЕНИЕ:Пара стабилизируется тогда и только тогда, когда диапазон содержит . Доказательство: Определить

.

Поскольку , взаимно просты, из этого следует [3], что . Пусть обозначает проекцию на вдоль , и пишем . Из (1)

(15)

где .

Поскольку являются -инвариантными подпространствами,

, .

Таким образом, (15) подразумевает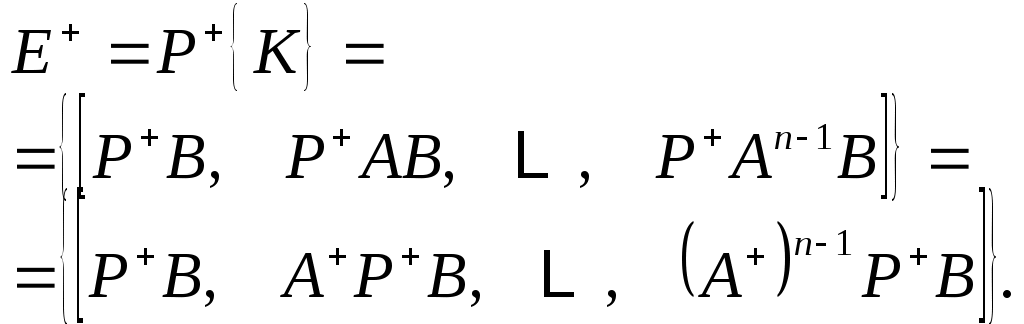

, (16)

где - ограничение на . Так же,



и здесь устойчив. Теперь, если тогда



Таким образом, пара является управляемой в , и существует матрица такая, что является устойчивой. Пусть и положим . потом



. (17)

Уравнение (17) показывает в треугольной форме со стабильными обоими диагональными блоками, то есть устойчиво.

Обратно предположим, что . Поскольку инвариантен и взаимно просты,

.

Таким образом, подпространство правильно содержится в ; другими словами, пара неуправляема. В обозначим через ортогональную проекцию на -инвариантное подпространство . Тогда , и . Запись

,

из (16) следует, что

.

Поскольку собственные значения включены в число значений , ясно, что подсистема с вектором состояния не может быть стабилизирована каким-либо выбором управления . Доказательство завершено.

Рассмотрим (l), определенный для , вместе со вспомогательным уравнением

, (18)

где представляет собой матрицу , а представляет наблюдаемый вектор. Определить -векторную функцию уравнением вида

,

(19)

где и будут определены ниже.

Функция может служить асимптотической оценкой в следующем смысле. Если пара стабилизируема, то матрицы и можно выбрать так, чтобы

,

для всех начальных значений . Действительно, выберите так, чтобы был стабильным, и установите . Тогда



и утверждение следует. Это означает, что если требуется только асимптотическая идентификация, то стабилизируемость может заменить более сильное условие наблюдаемости.

Основным результатом данной работы является доказательство эквивалентности управляемости и назначения полюсов в конечномерных динамических системах с вещественными параметрами. Таким образом, два упомянутых свойства проявляются в виде двойных понятий в соответствующих областях времени и частоты. Данное доказательство является длинным, но содержит интересный вспомогательный результат (лемма 3) и дает информацию о канонической структуре. Более слабое свойство стабилизируемости характеризуется как управляемость неустойчивых мод. Было бы интересно алгоритмизовать конструкцию смещения полюсов, возможно, по линии Басса и Гуры [6], и найти более точное абстрактное доказательство основной теоремы.
ЛИТЕРАТУРЫ

1. 
   S. Lefschetz, Stability of Nonlinear Control Systems. New York: Academic Press, 1965.
   
2. 
   C.E. Langenhop, “On the stabilization of linear systems,” Proc. Amer. Math. Soc., vol. 15, no. 5, pp. 735-742, 1964.
   
3. 
   F.R. Gantmacher, The Theory of Matrices, vol. 1. New York: Chelsea, 1959.
   
4. 
   G. Birkhoff and S. MacLane, A Survey of Modern Algebra. New York: Macmillan, 1953.
   
5. 
   R.E. Kalman, “When is a linear control system optimal?,” Trans. ASME, J. Basic Engrg., ser. D, vol. 86, pp. 51-66, 1964.
   
6. 
   R.W. Bass and I. Gura, “High order system design via state-space considerations,” Preprints, Joint Automatic Control Conf. (Troy, N. Y., June 1965), pp. 311-318.
   
7. 
   D. G. Luenberger, “Observers for multivariable systems,” IEEE Trans. Automatic Control, vol. AC-1l, pp. 190-197, -April 1966.
   
8. 
   J. D. Simon, private communication.
   

¹ Обозначение [.] обозначает диапазон матрицы.