Округление натуральных чисел 5 класс. Округление натуральных чисел. О правилах математического округления Приближенные значения
 Скачать 254.76 Kb. Скачать 254.76 Kb.
|
|
О правилах математического округления Приближенные значения В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться. У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения. Рассмотрим примеры: Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком. Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком. Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком. Приближенное значение — число, которое получилось после округления. Для записи результата округления используют знак «приблизительно равно» — ≈. Округлить можно любое число — для всех чисел работают одни и те же правила. Округлить число значит сократить его значение до нужного разряда, например, до сотен, десятков или тысяч, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна. Округление натуральных чисел Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее. Особенности натуральных чисел: Наименьшее натуральное число: единица (1). Наибольшего натурального числа не существует. Натуральный ряд бесконечен. У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7. Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями. Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление. Правила округления чисел: Подчеркнуть цифру разряда, до которого надо округлить число. Отделить все цифры справа от этого разряда вертикальной чертой. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1. Рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.  После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули. 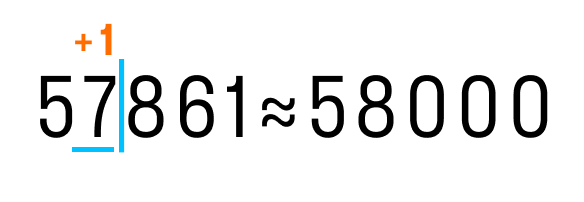 Теперь округлим 756 485 до сотен: 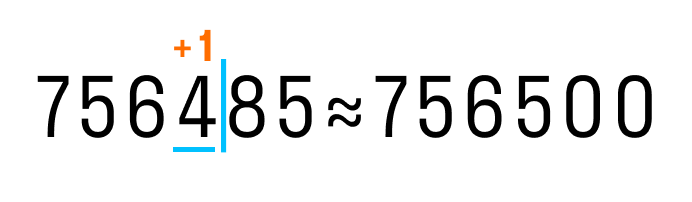 Округлим число 123 до десятков: 123 ≈ 120. Округлим число 3581 до сотен: 3581 ≈ 3580. Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1. Примеры: округлить число 697 до десятков — 697 ≈ 700; округлить число 980 до сотен — 980 ≈ 1000. ЗАПОМНИТЕ!  Самостоятельная работа 1. Округлите число до десятков: 175624 2. Округлите число до тысяч: 83754 3. Округлите число до миллионов: 13278518 4. Округлите число до десятков миллионов: 913278518 5. Округлите число до десятков миллиардов: 999913278518 6. На рынке купили 413 кг яблок, 13 кг груш и 282 кг слив. Сколько килограмм фруктов купили на рынке? Ответ округлите до сотен. 7. Длина прямоугольника равна 43 см, а его ширина – 601 см. Найдите периметр прямоугольника. Ответ округлите до метров.
|
