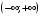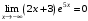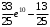Ответ. Область определения функции На всей области определения данная функция непрерывна. 2
 Скачать 77.42 Kb. Скачать 77.42 Kb.
|
|
Область определения функции. 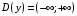 . .На всей области определения данная функция непрерывна. 2. Четность и периодичность функции. Так как у(-х)≠у(х), у(-х)≠-у(х), то функция не обладает свойствами четности или нечетности. Следовательно, график функции не симметричен ни относительно оси Оу, ни начала координат. Функция не является периодической, так как задана формулой 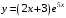 . .3. Исследуем поведение функции на концах области определения. 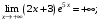 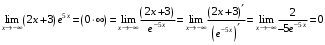 . .Асимптоты. Вертикальных асимптот нет. Если 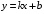 - наклонная асимптота, то - наклонная асимптота, то 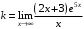 , , найдем 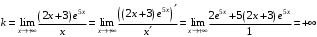 , ,значит, при 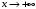 наклонных асимптот нет. наклонных асимптот нет.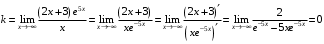 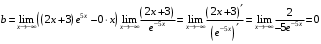 . .Значит, прямая у=0 – горизонтальная асимптота при 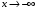 . .4. Промежутки монотонности и точки экстремума. Вычислим производную функции и найдем критические точки. 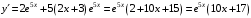 . .Производная существует при любых.  Решим уравнение 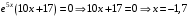 . .Следовательно, точка 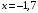 критическая. Найдем знак производной справа и слева от полученной точки. критическая. Найдем знак производной справа и слева от полученной точки.Значит, функция убывает при 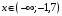 , и возрастает при , и возрастает при 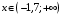 . .Отсюда следует, что 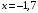 - точка минимума, - точка минимума, 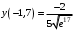 . .5. Промежутки выпуклости, вогнутости и точки перегиба. Найдем производную второго порядка от рассматриваемой функции 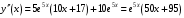 Вторая производная существует при любых значениях  . .Найдем точки, где 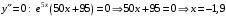 Найдем знак второй производной справа и слева от полученной точки. 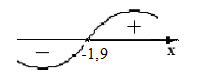 выпукла при 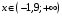 , вогнута при , вогнута при 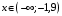 . . 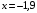 - точки перегиба, - точки перегиба, 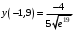 6. Найдем площадь фигуры, ограниченной графиком функции 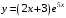 и прямыми х=0, х=2, у= 0. и прямыми х=0, х=2, у= 0.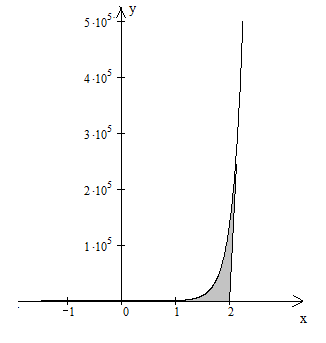 Для определения площади фигуры используем формулу 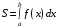 . .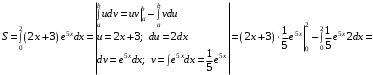 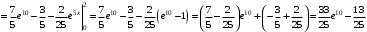
|