Задание. Обновить оборудование (полностью или частично), а
 Скачать 20.24 Kb.
|
|
Проведенные исследования срывов сроков выполнения работ компании ООО «Инженерные системы», выявили рост процента срывов сроков работ по нанесению огнезащитных покрытий. Анализ причин позволил выявить факторы, действия которых приводят к негативным последствиям. Для их нейтрализации важно: во-первых, обновить оборудование, во-вторых, увеличить штатный состав бригады, в-третьих, ввести личную финансовую заинтересованность работников. По результатам проведенного анализа руководству компании были предложены три стратегии: а1 – обновить оборудование (полностью или частично), а2 – увеличить штатный состав смены; а3 – ввести коэффициент и дополнительные доплаты за выполнение работ в установленные сроки. Матрица эффективности предлагаемых стратегий приведена в таблице 1. В качестве экспертов были приведены: К1 – внешний эксперт; К2 – главный инженер компании; К3 – заместитель директора по финансовой деятельности; К4 – мастер бригады с самым большим опытом работ по нанесению огнезащитных покрытий. В ячейки таблицы 1 проставлен процент, на который уменьшается количество срывов сроков работ по нанесению огнезащитных покрытий, то есть оценка эффективности применения соответствующих стратегий. Таблица 1. Матрица эффективности
Для оценки и выбора наиболее результативной стратегии использовать следующие критерии: критерий среднего выигрыша; критерий Лапласа; критерий Вальда; критерий «max-max»; критерий Гурвица и критерий Сэвиджа. Решение: критерий среднего выигрыша (критерий Байеса): По критерию Байеса за оптимальные принимается та стратегия ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r. Считаем значения 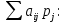 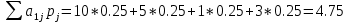 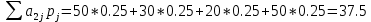 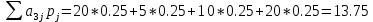 Выбираем из максимальный элемент 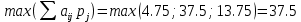 Следовательно, выбираем стратегию а2 – увеличить штатный состав смены. критерий Лапласа: В играх с природой если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.: q1 = q2 = q3 = q4 = ¼ = 0,25. Расчет 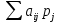 будет аналогичен с приведенным выше для критерия среднего выигрыша. Соответственно максимальный элемент будет соответствовать стратегии а2 – увеличить штатный состав смены.критерий Вальда: По критерию Вальда в качестве оптимальной принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е. 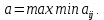 Критерий Вальда выражает пессимистическую оценку ситуации.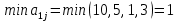 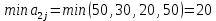 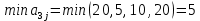 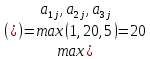 Следовательно, выбираем стратегию а2 – увеличить штатный состав смены. критерий «max-max»: Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации. 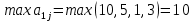 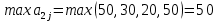 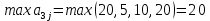 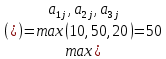 Выбираем стратегию а2 – увеличить штатный состав смены. критерий Гурвица: Критерий Гурвица является критерием пессимизма-оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение: 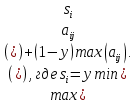 При y = 1 получим критерий Вальда, при y = 0 - критерий максимакс. y=0.5: 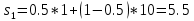 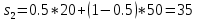 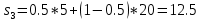 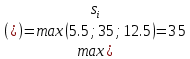 Выбираем стратегию а2 – увеличить штатный состав смены. критерий Сэвиджа: Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: 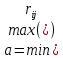 .Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков: r11 = 50 - 10 = 40; r21 = 50 - 50 = 0; r31 = 50 - 20 = 30. r12 = 30 - 5 = 25; r22 = 30 - 30 = 0; r32 = 30 - 5 = 25. r13 = 20 - 1 = 19; r23 = 20 - 20 = 0; r33 = 20 - 10 = 10. r14 = 50 - 3 = 47; r24 = 50 - 50 = 0; r34 = 50 - 20 = 30.
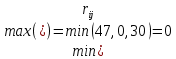 Выбираем стратегию а2 – увеличить штатный состав смены. Ответ: единственно верным решением является выбор стратегии увеличения штатной численности работников смены. |