Квадратные неравенства. квадратные неравенства. Оборудование учебный комплект Алгебра8 А. Г. Мордковича, тетрадь, карандаш, авторучка, линейка, компьютер, медиапроектор, интерактивная доска Interwrite Board. Программное
 Скачать 64.22 Kb. Скачать 64.22 Kb.
|
|
Цели: ввести понятие квадратного неравенства; познакомить учащихся с алгоритмом квадратного неравенства; формировать умение решать квадратные неравенства. Оборудование: учебный комплект “Алгебра-8” А. Г. Мордковича, тетрадь, карандаш, авторучка, линейка, компьютер, медиапроектор, интерактивная доска Interwrite Board. Программное обеспечение: Windows XP, MS PowerPoint-2003 (2007), программа для работы с интерактивной доской InterwriteTM Workspace. I. Организационный момент. II. Актуализация опорных знаний. Учитель: (слайд №1) перед вами несколько математических выражений. Скажите, какие из них вам знакомы, как они называются и выделите те, которые вам пока не знакомы. 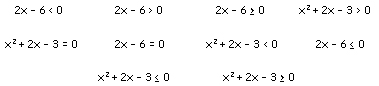 (Линейные уравнения и неравенства и квадратное уравнение знакомы; незнакомы - квадратные неравенства. На интерактивной доске перетаскиваем знакомые уравнения и неравенства на книжную полку (уже “прочитанные книги”), а незнакомые – на раскрытую книгу (предстоит “прочитать”). Рисунок книжной полки появляется после щелчка). Итак, ребята, как вы думаете, что перед нами, “какую книгу нам предстоит прочитать”? Учащиеся: квадратные неравенства. Учитель: тема сегодняшнего урока “Решение квадратных неравенств”. (Cлайд №2) III. Этап ориентировки в новом материале и способах работы с этим материалом (“ориентировка”). Учитель: Назовите общий вид квадратных неравенств ( по аналогии с квадратными уравнениями). Учащиеся: Учитель: вместо знака “>”, можно использовать любой другой знак неравенства. Как же решить квадратное неравенство Учащиеся: перечисляют варианты. Учитель подводит их к мысли, что надо попробовать решить графически, т. е. построить график функции y = x2 + 2x – 3 (параболу). После чего надо будет ответить на вопрос: для каких значений хy>0? Построение параболы: (Слайд №4) вершина параболы x0 = -1, y0 = -4 точки пересечения с осью OX: для этого решаем квадратное уравнение x2 + 2x – 3 = 0 х1 = -3, х2 = 1 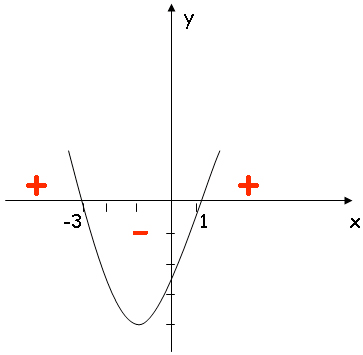 Здесь надо обратить внимание на главные точки (точки пересечения параболы с осью ОХ) и главные числа -3 и 1 (абсциссы точек пересечения параболы с осью ОХ). Учитель: Ответить на вопрос нам помогут знаки “+” и “-”, которые мы поставим на координатной плоскости (“+”: y>0 парабола выше оси ОХ; “-”: y<0 парабола ниже оси ОХ). Итак, решением неравенства Является объединение промежутков Далее с помощью данного рисунка решим оставшиеся 3 неравенства. (Слайд №4) (Здесь надо обратить внимание на промежутки, которые выбираем в качестве ответа и скобки, которые надо поставить в зависимости от того, строгое неравенство или нестрогое). После этого учитель вместе с учащимися формулирует алгоритм решения квадратного неравенства (с записью в тетради). (Слайд №5) (Здесь надо обратить внимание учащихся на то, что находить вершину параболы необязательно, достаточно найти точки пересечения о осью ОХ и знать куда направлены ветви параболы. Т. е. строим параболу почти схематически (за исключением точек пересечения с осью ОХ), используя при этом только ось ОХ (см. рисунок ниже). 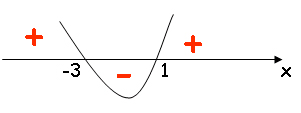 IV. Этап “продконтрольного оперирования”. На данном этапе решим 4 неравенства, проговаривая и объясняя каждый шаг алгоритма. а) -2x2 + 3x + 9 < 0 б) 4x2 - 4x + 1 <0 в) 2x2 – x + 4 > 0 г) -x2 + 3x – 8 > 0 (-) Решение: а) -2x2 + 3x + 9 < 0 1) -2x2 + 3x + 9 = 0 х1 = 3, х2 = -1,5 - ветви параболы направлены вниз. 2) Cтроим схематически параболу. 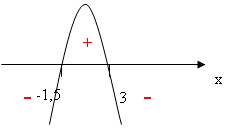 3) Ответ: (-оо; -1,5) Примечание: над знаком неравенства полезно поставить знак “+” или “-” и взять его, в зависимости от знака неравенства, либо в круглые, либо в квадратные скобки. Также на рисунке можно использовать штриховку. б) 4x2 - 4x + 1 < 0 Особенность этого неравенства в том, что квадратное уравнение имеет один корень х = 0,5, значит парабола с осью ОХ имеет только одну общую точку. Надо изобразить схематически параболу и обсудить то, что решением неравенства будет одно число. Ответ: х = 0,5 в) 2x2 – x + 4 > 0 Квадратное уравнение корней не имеет. Парабола с осью ОХ не имеет точек пересечения, она расположена целиком выше оси ОХ. Ответ: (-оо;+ оо). г) -x2 + 3x – 8 > 0 Квадратное уравнение корней не имеет. Парабола с осью ОХ не имеет точек пересечения, она расположена целиком ниже оси ОХ. Ответ: решений нет. IV. Этап постепенного снятия контроля (переход к самоконтролю). На этом этапе формируем навык решения квадратных уравнений. Работаем с задачником № 34.3 – 34.10 (по одному неравенству). №34.23 (а, б) №34.24 (а, б) V. Итог урока: проговорить алгоритм решения квадратного неравенства. Оценки за урок тем учащимся, которые активно участвовали в обсуждении новой темы. VI. Домашнее задание: |
