расчет фермы. Обозначаем буквами узлы и стержни. Из геометрии определяем значения углов между стержнями
 Скачать 240.63 Kb. Скачать 240.63 Kb.
|
|
Вариант 14. Исходная схема: 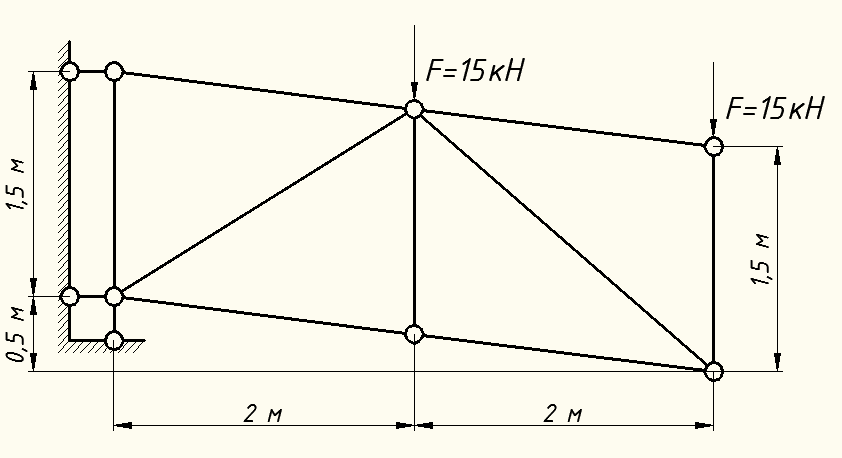 Обозначаем буквами узлы и стержни. Из геометрии определяем значения углов между стержнями. 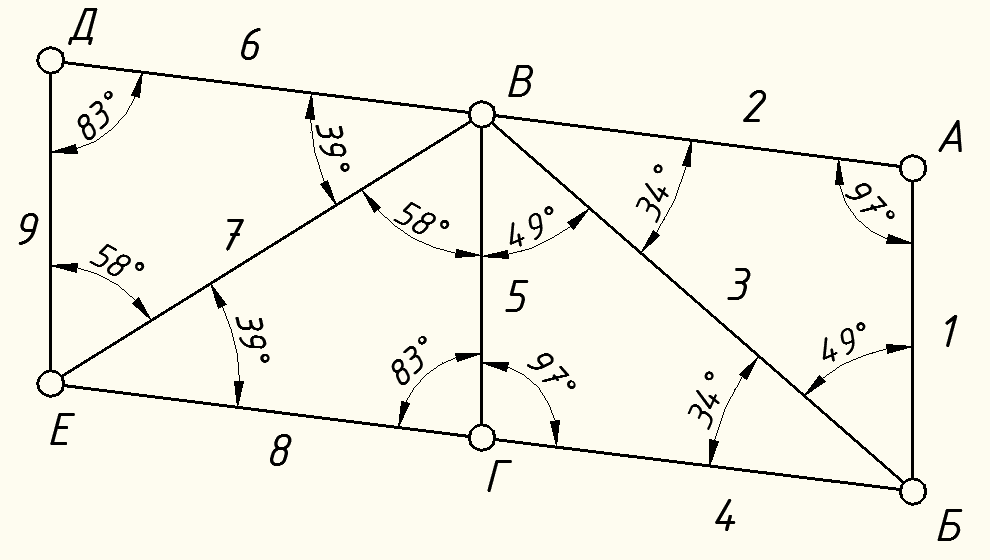 Аналитический метод решения задачи 1. Вырезаем узел А. 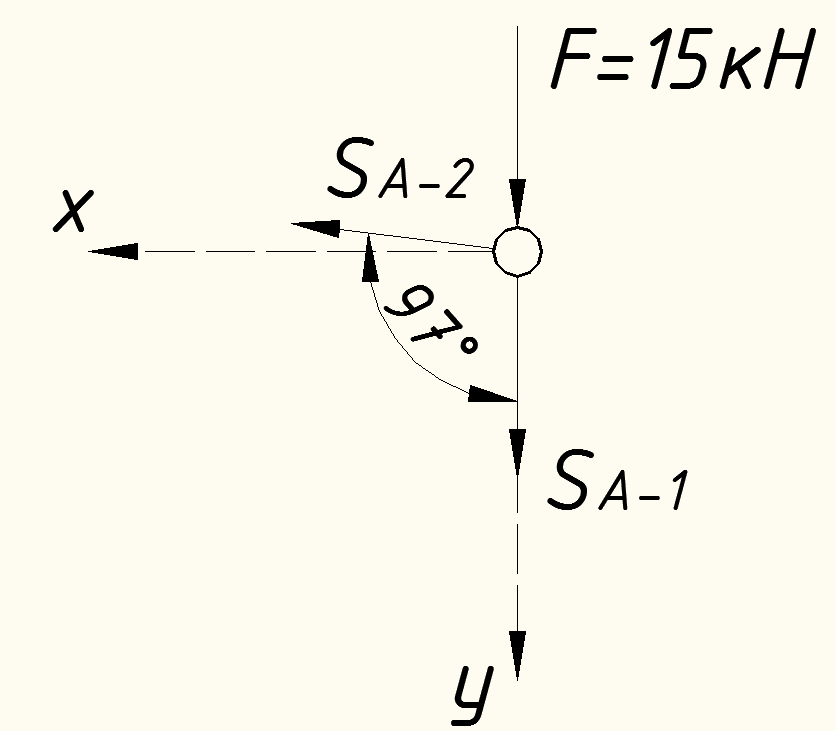 Неизвестные реакции в стрежнях 1 и 2 обозначим как 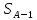 и и 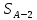 . Ось координат Х направим вдоль стержня 1. Из условия статического равновесия: . Ось координат Х направим вдоль стержня 1. Из условия статического равновесия: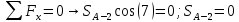 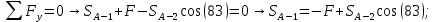 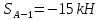 2. Вырезаем узел Б. 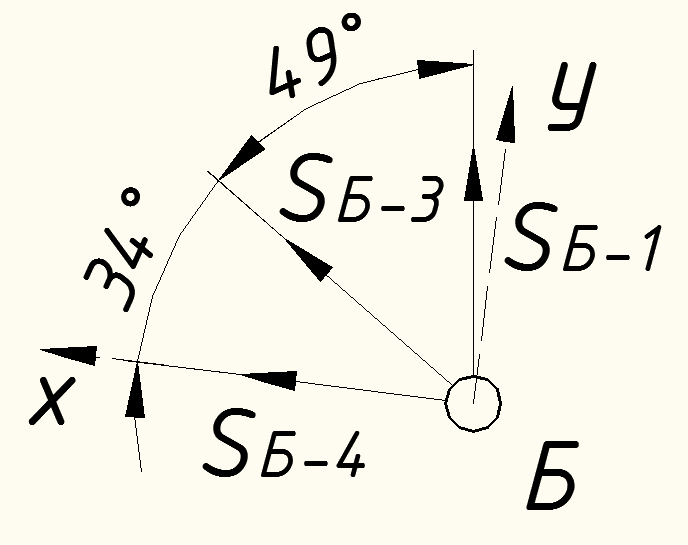 Неизвестные реакции в стрежнях 3 и 4 обозначим как 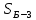 и и 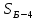 . Реакция в стрежне . Реакция в стрежне 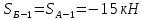 . Ось координат Х направим вдоль стержня 4. Из условия статического равновесия: . Ось координат Х направим вдоль стержня 4. Из условия статического равновесия: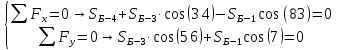 Решая данную систему, получим: 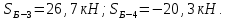 3. Вырезаем узел В. 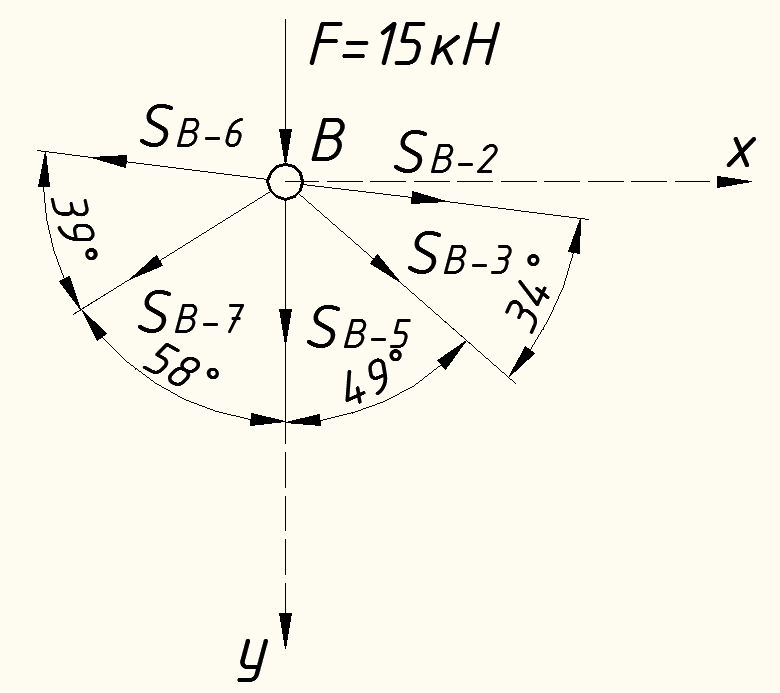 Неизвестные реакции в стрежнях 5,6,7 обозначим как 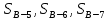 . Реакция в стрежне . Реакция в стрежне 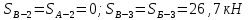 . Оси координат У направим вдоль стержней 5. . Оси координат У направим вдоль стержней 5.Из условия статического равновесия: 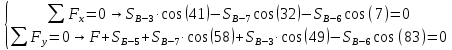 Получили систему из 2 уравнений с 3 неизвестными. Найдем усилие в стрежне 6 методом сечений. Для этого проведем сечение через стрежни 6,7,8, отбросим левую его часть, заменив при этом отброшенную часть реакциями в стрежнях. 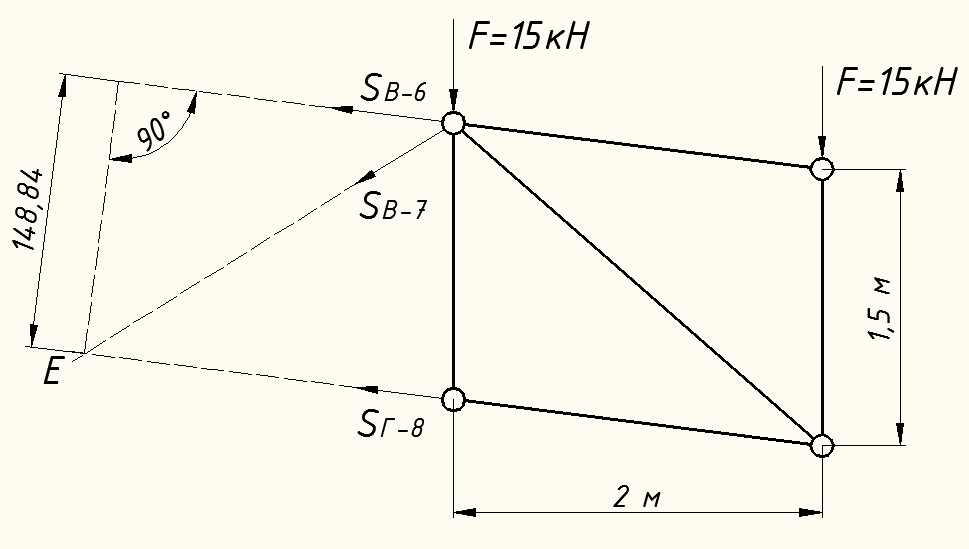 Реакции в стрежнях 7 и 8 сходятся в точке Е. Из условия статического равновесия относительно точки Е получим: 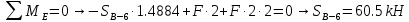 Тогда, 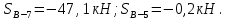 4. Вырезаем узел Г. 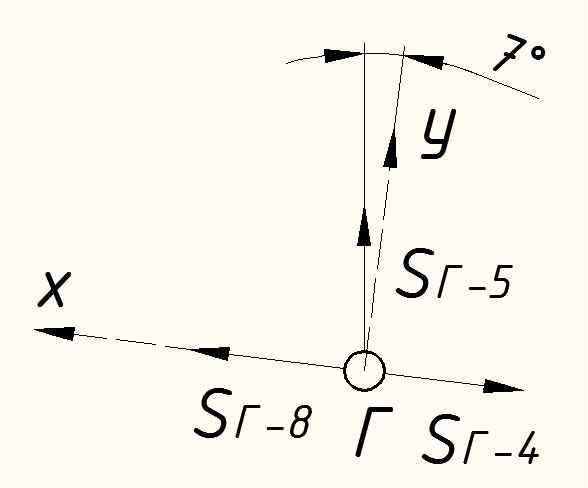 Неизвестную реакцию в стрежне 8 обозначим как 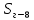 . Реакция в стрежне . Реакция в стрежне 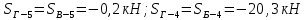 . Ось координат Х направим вдоль стержня 8. . Ось координат Х направим вдоль стержня 8.Из условия статического равновесия: 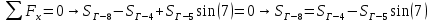 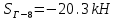 Графический метод решения задачи Для решения задачи графическим методом выбираем на чертеже масштаб силы F (100 мм = 10 кН) и для каждого узла строим замкнутый треугольник сил, стороны которого в выбранном масштабе будут изображать силы. Для узла А: 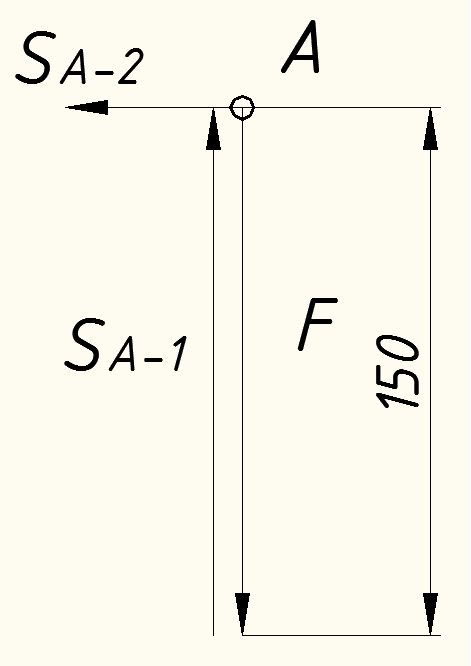 Из данной диаграммы сил видно, что 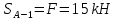 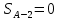 . .Для узла Б: 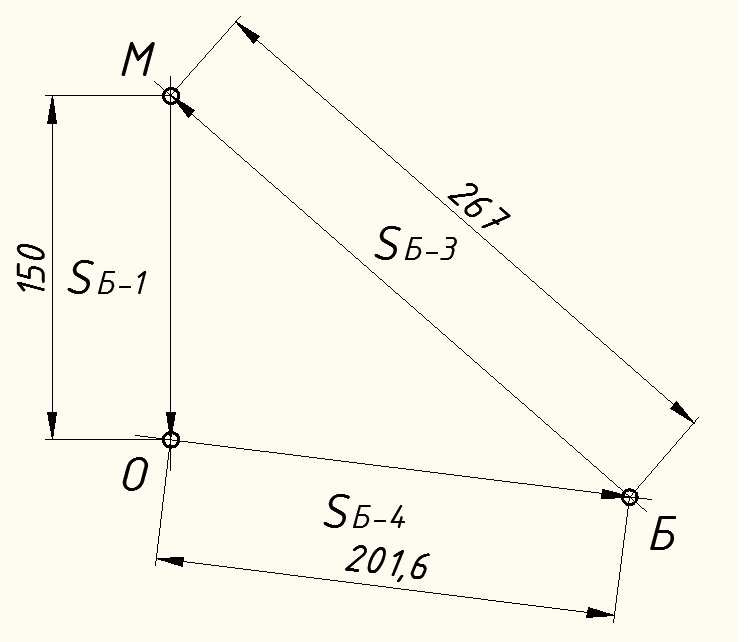 Реакция 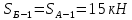 . Из треугольника ОБМ находим: . Из треугольника ОБМ находим: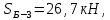 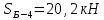 . .Для узла В: 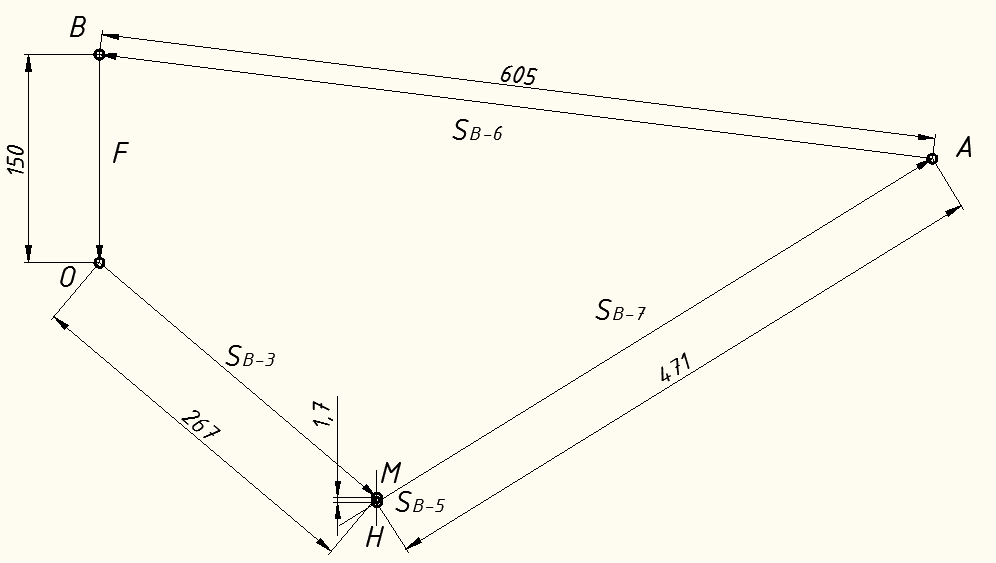 Реакция 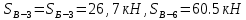 . Из многоугольника АВОМН находим: . Из многоугольника АВОМН находим: 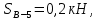 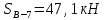 . .Для узла Г:  Реакция 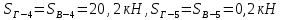 . Из треугольника ГМН находим: . Из треугольника ГМН находим: 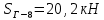 . .Результаты, найденные аналитическим и графическим способами, совпалают! |
