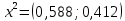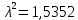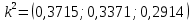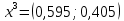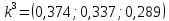обработка экспертных систем. Лабараторная №1 Обработка экспертных оценок - копия. Обработка экспертных оценок методом непосредственной оценки
 Скачать 25.44 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА И ГОСУДАРСТВЕННОЙ СЛУЖБЫ при ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»  Балаковский филиал РАНХиГС Факультет государственно-правового управления Направление подготовки 09.03.03 Прикладная информатика Профиль Прикладная информатика в менеджменте Кафедра Гуманитарных и естественно- научных дисциплин управления Практическая работа №1 на тему: «Обработка экспертных оценок методом непосредственной оценки» Автор работы: студент 4 курса заочной формы обучения Демин Денис Викторович подпись_________________________ Руководитель работы: доцент кафедры гуманитарных и естественно-научных дисциплин, кандидат технических наук Козлова Татьяна Дмитриевна Оценка_________________________ Подпись ________________________ Балаково 2022 г. Вариант №4
Три эксперта (m=3) оценили значение двух мероприятий (n=2) по степени их влияния на решение одной из проблем (l=1). Результатами экспертизы явились нормированные оценки мероприятий x1j+x2j=1, j=1,2,3, в соответствии с таблицей. Вычислим групповые оценки мероприятий, приводящих к решению проблемы и коэффициенты компетентности каждого из экспертов. Для этого воспользуемся приведенным выше алгоритмом, задавшись точностью вычисления Е=0,001. В соответствии с формулами (1,2) получим средние оценки объектов первого приближения (при t=1): 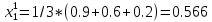 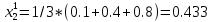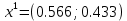(1)  (2)   – средние оценки объектов первого приближения на первом шаге.Используя формулу, вычислим нормировочный коэффициент 1: 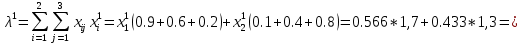 1,525Значения коэффициентов компетентности первого приближения, в соответствии с формулой (3): 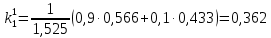 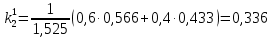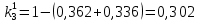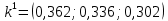(3)    Вычисляя групповые оценки второго и т. д. приближения, получим: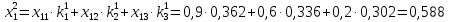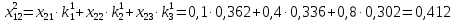  
Результат третьего шага удовлетворяет условию окончания итерационного процесса и за значение групповой оценки принимается xx3 = (0,595; 0,405). | |||||||||||||||||||
