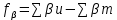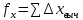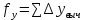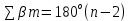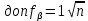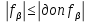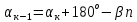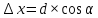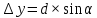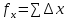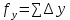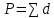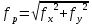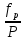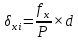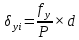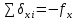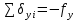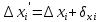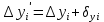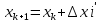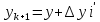КР1 Обработка материалов геодезических измерений, выполненных при создании планового съёмочного обоснования. КР1 Пояснительная записка. Обработка материалов геодезических измерений, выполненных при создании планового съёмочного обоснования
 Скачать 36.22 Kb. Скачать 36.22 Kb.
|
|
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения (УрГУПС) Кафедра «Мосты и транспортные тоннели» КОНТРОЛЬНАЯ РАБОТА № 1 на тему: «Обработка материалов геодезических измерений, выполненных при создании планового съёмочного обоснования» Проверил Выполнил Доцент Студент группы: ЭД-140 Лазарев С. Г. Никитин Е.П. Екатеринбург 2021 г. Содержание1. Введение 2 1.1 Цели 2 1.2 Задачи 2 2. Теоретическая часть 3 2.1 Исходные данные для выполнения работы 3 2.2 Уравнивание теодолитного хода 3 2.3 Уравнивание горизонтальных углов 4 2.4 Уравнение дирекционных углов сторон хода 5 2.5 Уравнивания приращений координат 5 2.6 Уравнения координат точек хода 7 3. Расчётная часть 8 3.1 Расчёт уравнивания теодолитного хода 8 3.2 Уравнивание горизонтальных углов 8 3.3 Расчёт дирекционных углов сторон хода 9 3.4 Расчёт и уравнивание приращений координат 9 3.5 Расчёт координат точек хода 12 5. Заключение 13 1. Введение Геодезическое съемочное обоснование – это система закрепленных на местности точек, координаты которых известны. С точек съемочного обоснования производится съемка местности. Плановое съемочное обоснование для различных видов топографической съемки обычно создают прокладкой теодолитных ходов. При прокладке теодолитных ходов в поле измеряют длины линий между точками с точностью 1:2000 и углы между сторонами хода с точностью 30''. Для вычисления координат точек в принятой на объекте системе координат выполняют геодезическую привязку хода к пунктам геодезических опорных сетей, т.е. определяют координаты начальной точки и дирекционный угол начальной стороны хода. После окончания полевых измерений производят их камеральную обработку. Вычисления выполняют с помощью микрокалькуляторов или ЭВМ, используя электронную таблицу Excel. 1.1 Цель: 1.1.1 Используя исходные данные, включающие измеренные углы точек, дирекционный угол первой точки, горизонтальные приложения и приращения координат, провести расчёты координат точек съёмочного обоснования. 1.2 Задачи: 1.2.1 Вычислить уравненные горизонтальные углы (правые); 1.2.2 Рассчитать дирекционные углы всех точек съёмочного обоснования; 1.2.3 Выяснить приращения координат; 1.2.4 Определить координаты всех точек съёмочного обоснования. 2 Теоретическая часть 2.1 Исходные данные для выполнения работы (вариант 18) При создании планового съемочного обоснования был проложен замкнутый теодолитный ход из четырех точек. Исходными данными для выполнения работы являются: внутренние (правые по ходу) горизонтальные углы β на точках хода, горизонтальные проложения d сторон, координаты х1 = 1900, у1 = 2100 первой (начальной) точки хода и дирекционный угол α1-2 = 215°20´ первой (начальной) стороны хода. Схема геодезического хода показана на рис.1. 2.2 Уравнивание теодолитного хода Уравнивание – это процесс обработки результатов измерений, при котором: 1) производят контроль и оценку качества выполненных измерений; 2) находят наиболее вероятные значения измеренных величин (углов, линий) и их функций (дирекционных углов линий, координат точек). Решение первой части задачи уравнивания состоит в определении невязок и оценке их допустимости. Решение второй части состоит: - в распределении невязок, т.е. в нахождении по определенным правилам поправок к измеренным и вычисленным величинам; - в вычислении уравненных значений искомых величин. В замкнутом теодолитном ходе три избыточных измерения (два угла и одна линия), которые приводят к возникновению трех геометрических условий. Эти условия можно записать в виде трех условных уравнений: - угловая невязка хода:
где: 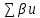 – сумма измеренных углов хода (истинная); – сумма измеренных углов хода (истинная);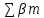 – сумма углов хода (теоретическая). – сумма углов хода (теоретическая).- невязка приращения координат x:
- невязка приращения координат у:
2.3 Уравнивание горизонтальных углов Уравнивание горизонтальных углов выполняются в следующем порядке: 1. Вычисляют сумму измеренных углов 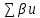 ; ;2. Вычисляют теоретические значения 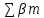 суммы углов хода по формуле: суммы углов хода по формуле:
где: n – число точек хода, n = 4 (вариант 3) 3. вычисляют угловую невязку по формуле 1; 4. Вычисляют допустимое значение угловой невязки по формуле:
5. Сравнивают полученную невязку (формула 1) с допустимой (формула 2). Идеальный расчёт должен отвечать требованию:
6. Вычисление уравненных значений углов и их сумму, которая должна равняться 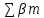 . .2.4 Вычисление дирекционных углов сторон хода Дирекционные углы сторон хода вычисляют по заданному дирекционному углу стороны 1-2 и уравненным значениям горизонтальных (правых) углов по формуле:
где: 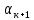 - дирекционный угол последующей стороны хода; - дирекционный угол последующей стороны хода;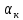 – дирекционный угол предыдущей стороны; – дирекционный угол предыдущей стороны;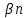 - правый горизонтальный угол между этими сторонами. - правый горизонтальный угол между этими сторонами.2.5 Вычисление и уравнивание приращений координат Приращения координат вычисляются с помощью микрокалькулятора по формулам:
где: d – горизонтальное проложение стороны хода; 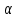 – дирекционный угол той же стороны. – дирекционный угол той же стороны.Вычислительные значения приращений округляют до 0,01 м. В суммарной строке этих же граф находят координатные невязки ƒx и ƒу :
Далее записывают суммарное значение периметра хода P (сумма всех длин сторон хода) с точностью до метра:
Для оценки допустимости координатных невязок 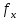 и и 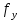 вычисляют абсолютную невязку в периметре хода: вычисляют абсолютную невязку в периметре хода:
и относительную невязку:
Относительную невязку выражают дробью с числителем, равным 1. Сравнивают полученную относительную невязку с допустимой, которая равна 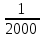 . .Если относительная невязка недопустима, т.е. если знаменатель невязки меньше 2000, то проверяют правильность вычисления дирекционных углов и приращений координат, правильность их суммирования. Если относительная невязка допустима, то допустимы и координатные невязки 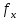 и и 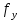 . Их распределяют с обратным знаком по всем приращениям прямо пропорционально длинам горизонтальным положениям сторон хода, т.е. вычисляют правки . Их распределяют с обратным знаком по всем приращениям прямо пропорционально длинам горизонтальным положениям сторон хода, т.е. вычисляют правки 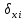 , , 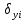 по формулам: по формулам:
Контроль вычисления поправок:
Если этот контроль не выполняется на 1-2 см, то вычисленные поправки 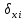 и и 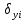 следует округлить так, чтобы суммы поправок точно равнялись невязкам с обратным знаком. Уравненные значения ∆xi′ и ∆yi′ приращений координат, учитывая знак приращения и поправки рассчитывается по формулам: следует округлить так, чтобы суммы поправок точно равнялись невязкам с обратным знаком. Уравненные значения ∆xi′ и ∆yi′ приращений координат, учитывая знак приращения и поправки рассчитывается по формулам:
Контроль вычислений: суммы уравненных приращений должны точно равняться нулю ∑∆х=0, ∑∆у=0. Если этот контроль не получается, то следует проверить правильность вычисления невязок ƒ x и ƒy, знаки поправок 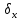 и и 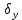 ,учет этих знаков при вычислении уравненных приращений. ,учет этих знаков при вычислении уравненных приращений.2.6 Вычисление координат точек хода По заданным координатам точки 1 и уравненным приращениям координат вычисляют координаты всех точек хода:
3 Расчётная часть 3.1 Расчёт уравнивания теодолитного хода Чтобы произвести выравнивание теодолитного хода, я рассчитал угловую невязку хода по формуле 1 и предварительно вычислил сумму углов хода (теоретическую) по формуле 4 и суму измеренных углов хода (истинную). Из условий, которые приведены в таблице 1 следует, что горизонтальные углы четырёх (n = 4) точек теодолитного хода 2, 3, 4 и 1 соответственно равны 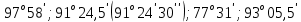 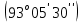 , следовательно: , следовательно:Угол точки 3 = 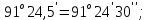 Угол точки 1 = 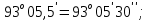 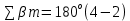 = = 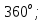 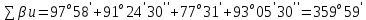 ; ;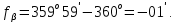 Далее я вычислил допустимое значение угловой невязки по формуле 5 и сравнил полученную невязку с угловой (формула 1) по формуле 6: 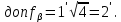 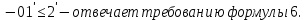 2.2 Уравнивание горизонтальных углов Для расчёта уравненных значений углов и их суммы, которая должна равняться 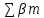 я разделил полученную угловую невязку (формула 1) на количество точек теодолитного хода, чтобы распределить полученные значения на измеренные горизонтальные углы: я разделил полученную угловую невязку (формула 1) на количество точек теодолитного хода, чтобы распределить полученные значения на измеренные горизонтальные углы: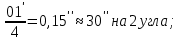 Уравненный угол точки 3 = 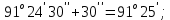 Уравненный угол точки 1 = 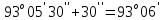 . .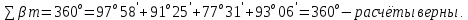 2.3 Расчёт дирекционных углов сторон хода Расчёт дирекционных углов я производил по формуле 7 с применением уравненных горизонтальных углов. Исходя из условий третьего варианта контрольной работы, первый дирекционный угол 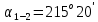 . .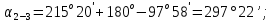 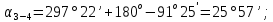 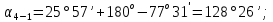 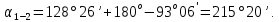 Конечное значение совпадает с исходными данными, что говорит о правильности проведённых расчётов. 3.4 Расчёт и уравнивание приращений координат Для каждой точки теодолитного хода рассчитывал приращения координат по формулам 8 и 9. Исходя из условий, указано, что горизонтальные проложения точек 2, 3, 4 и 1 соответственно равны 135,48 м, 163,02 м, 170,80 м, 189,70 м, следовательно: 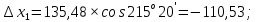 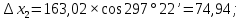 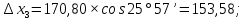 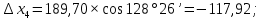 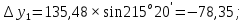 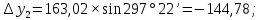 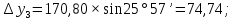 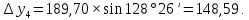 Следующим шагом я вычислил суммы рассчитаных приращений координат x и y по формулам 10 и 11, а так же значение периметра хода P (сумма всех длин сторон хода) по формуле 12: 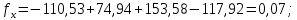 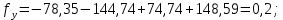 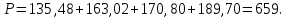 Для оценки допустимости координатных невязок 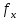 и и 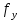 я вычислил абсолютную невязку в периметре хода по формуле 13 и далее относительную невязку по формуле 14: я вычислил абсолютную невязку в периметре хода по формуле 13 и далее относительную невязку по формуле 14: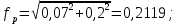 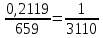 . .Сравнил полученную относительную невязку с допустимой, которая равна 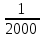 : :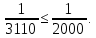 Полученный результат говорит о том, что относительная невязка является допустимой, т.к. её знаменатель больше 2000. Так же этого говорит о том, что допустимыми являются координатные невязки 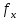 и и 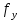 . .Для уравнения вычисленных приращений координат точек теодолитного хода я вычислил правки 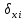 , , 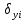 по формулам 15 и 16 провёл контроль вычисления поправок по формулам 17 и 18. Затем рассчитал уравненные приращения координат: по формулам 15 и 16 провёл контроль вычисления поправок по формулам 17 и 18. Затем рассчитал уравненные приращения координат: 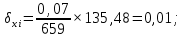 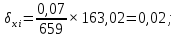 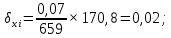 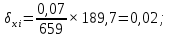 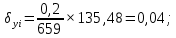 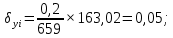 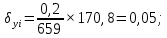 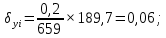 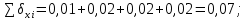 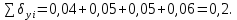 Погрешности контроля не превышают 1-2 см, т.е. вычисленные поправки 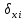 и и 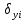 верны. верны.Следующим шагом я рассчитал уравненные значения приращений координат по формулам 19 и 20: 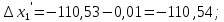 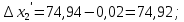 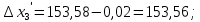 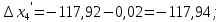 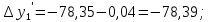 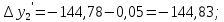 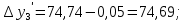 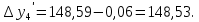 Контроль вычислений должен был показать, что суммы полученных значений равны нулю: 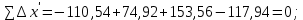 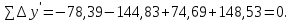 3.5 Расчёт координат точек хода По заданным координатам точки 1, которые равны x = 1900 y = 2100 и уравненным приращениям координат я вычислил координаты всех точек хода: 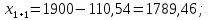 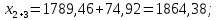 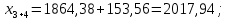 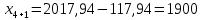 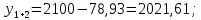 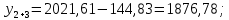 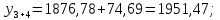 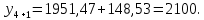 Погрешность измерений не превысила 2 см, что говорит о верности вычислений. 5. Заключение В обработка материалов геодезических измерений я рассчитал все дирекционные углы, вычислил приращения координат, их уравненные значения, а также координаты всех данных точек. Все итоговые вычисления приведены в таблице 1. Построение точек теодолитного хода представлены на рисунке 2. |