Лабораторная работа. Лабораторная работа 1. Обработка результатов эксперимента 1

• Название: Обработка результатов эксперимента 1
• Анкор: Лабораторная работа
• Дата: 02.04.2021
• Размер: 109.55 Kb.
• Имя файла: Лабораторная работа 1.docx
• Тип: Документы; #190725

Обработка результатов эксперимента

1)

Рассчитаем удельное сопротивление металлических проводников, используя соотношение

ρ = RS/l,

где R – сопротивление образца; S – площадь поперечного сечения; l – длина проводника. Например ρ =(106,34*(ℼ*(0,0001/2)^2)/1,53)*10^6=0,54 мкОм*м

Рассчитаем сопротивление квадрата поверхности металлических пленок

R_□ = Rb/l,

где R – сопротивление образца; b и l – ширина и длина пленочного резистора соответственно. Например

R_□ = 41,92*2,5/0,2=524 Ом
Таблица 1.1- расчёта сопротивлений квадарата поверхности металлических плёнок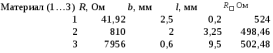



Таблица 1.2- расчёта удельного мопротивления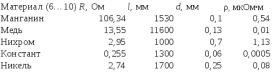



2)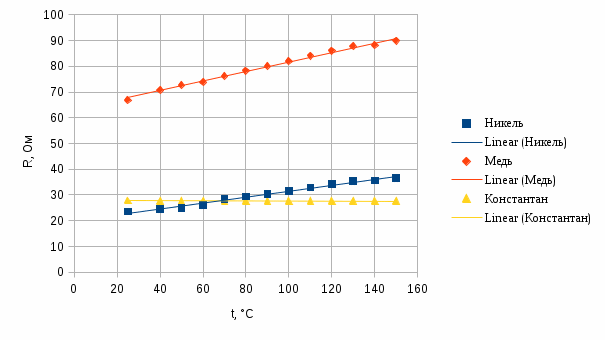
рисунок 1-температурные зависимости сопротивления R=f(t) для исследованных резисторов.

3)

Рассчитать температурный коэффициент удельного сопротивления металлов и сплавов как

α_ρ = α_R + α_l,

где α_R и α_l – температурные коэффициенты сопротивления и линейного расширения соответственно.

Температурный коэффициент сопротивления при данной температуре рассчитать по выражению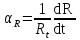

,

где R – сопротивление образца при данной температуре.

Так как зависимость R(t), исследованных образцов, можно аппроксимировать линейной зависимостью, то отношение ΔR/Δt остается постоянным во всем интервале температур: для меди – 0,2 Ом/ К^–1 ; никеля – 0,11^. 10⁻⁶ Ом/ К^–1, константана – -0,001 Ом/ К^–1.

Температурные коэффициенты линейного расширения имеют следующие значения: для меди – 16,7 ^. 10⁻⁶ К^–1; никеля – 12,8 ^. 10⁻⁶ К^–1, константана – 17,0 ^. 10⁻⁶ К^–1.

Рассчитаем темепературный коэффициент удельного сопротивления для меди

α_ρ = 0,2*(1/40)+16,7 ^. 10⁻⁶ =0,0052 К<sup>–1

Таблица 1.3-определения температурных зависимостей сопротивления
проводников</su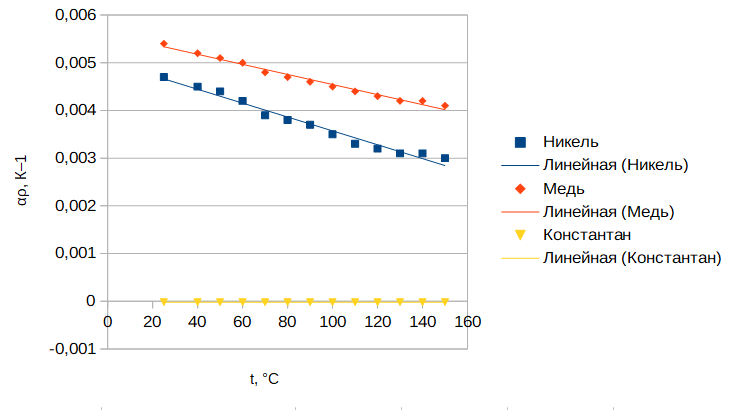p>



4)

^{р исунок 2- зависимость α}_ρ <sup>= f(t) для исследованных материалов.

5)</sup>

Значения удельного сопротивления сплавов могут быть получены по приближенной формуле

^ρ_Cu-Ni ^{= ρ}_Ni^х_Ni ^{+ ρ}_Сu ^(1−х_Ni^{) + С х}_Ni^(1−х_Ni<sup>),

где С – постоянный коэффициент; х</sup>_Ni ^{– содержание никеля в сплаве в относительных долях по массе; х}_Ni ^{+ х}_Cu <sup>= 1.

Найдём константу С при х</sup>_Ni =0,4 , С=(0,48-0,1*0,4-0,0175*0,6)/(0,6*0,4)≈ 2 мкОм∙м

Рассчитаем ^ρ_Cu-Ni ^{, для х}_Ni =0,2 ^ρ_{Cu-Ni =0,1*0,2+0,0175*0.8} +2*0,2*0,8≈0,3 мкОм∙м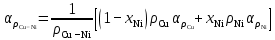

Значения температурного коэффициента удельного сопротивления сплавов Cu-Ni при различных содержаниях никеля могут быть приближенно рассчитаны по формуле

,

где 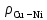− удельное сопротивление сплава соответствующего состава.

Например при х_Ni =0

α_ρ=(1*0,0175*0.0054)/0,0175=0,0054 К^–1

Таблица 1.5-

расчёта зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава .

хNi	0	0,2	0,4	0,6	0,8	1,0
ρ, мкОм∙м	0,0175	0,3	0,48	0,5	0,37	0,1
αρ , К–1	0,0054	0,001	0,001	0,001	0,0011	0,005

6)





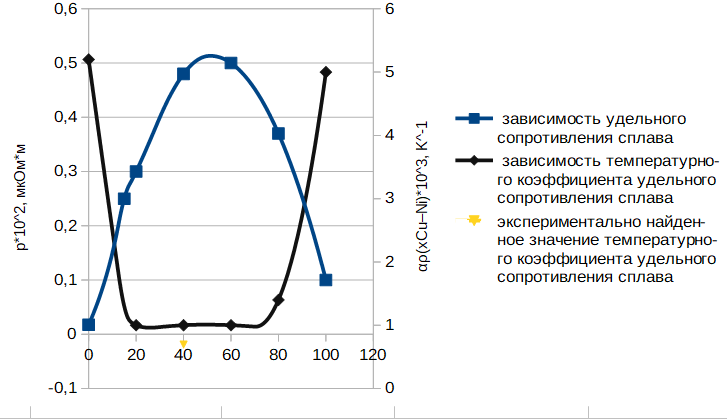рисунок 3-зависимости удельного сопротивления сплава ρ_Cu–Ni и температурного коэффициента удельного сопротивления сплава α_ρ(хCu–Ni

7)

Таблица 1.4-температурной зависимости термоЭДС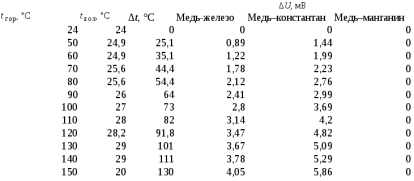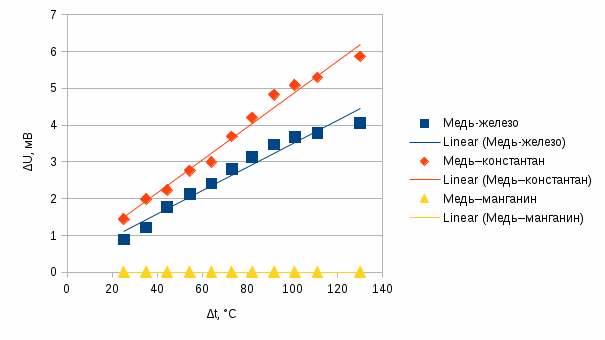






рисунок 4- температурные зависимости термоЭДС ΔU( 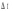) для исследованных термопар
Вывод

В данном опыте были рассчитаны удельные сопротивления металлических проводников и тонких плёнок .Вследствие поверхностного рассеяния электронов и повышенной степени дефектности структуры удельное сопротивление тонких металлических пленок существенно превосходит удельное сопротивление объемного материала, что и подтверждают данные таблиц 1.1 и 1.2.

При изучении ^{температурных зависимостей сопротивления
проводников были составлены графики, на которых видно, что сопротивление меди и никеля растёт с повышением температуры из-за рассеяния электронов на тепловых колебаниях решётки (с повышением температуры увеличивается амплитуда колебаний атомов в узлах кристаллической решетки, что приводит к более интенсивному рассеянию электронов в процессе их направленного движения).Сопротивление константана (его компонентами являются металлы переходной группы) почти не изменяется с повышением температуры, что связано с тем, что в концентрированных твёрдых растворах p}_ост значительно превышает ^p_т . Это связано с переходом части валентных электронов на внутренние незаполненные d-оболочки атомов переходной группы.

По графику зависимости удельного сопротивления медно-никелевого сплава и температурного коэффициента удельного сопротивления можно, сказать что чем больше удельное сопротивление сплава тем меньше температурный коэффициент удельного сопротивления. Изменение ρ_Cu–Ni и α_ρ(хCu–Ni) от процентного содержания компонентов сплава,можно объяснить тем, что изменение проводимости сплавов обуславливается не только изменением длины свободного пробега электронов, но и частичным возрастанием концентрации носителей заряда при повышении температуры.

ТермоЭДС первых двух термопар с ростом температуры возрастает, так как возрастает разность температур. Медь-манганин имеет очень малую удельную электродвижущую силу, в связи с чем этот сплав наиболее подходящий, среди рассмотренных, для приборов с высоким классом точности или для приборов предназначенных для измерений малых напряжений.


Вопросы

1. Почему металлы обладают высокой электрической проводимостью?

2. Чем обусловлено возрастание удельного сопротивления металлов при нагревании?

3. Почему удельное сопротивление металлических сплавов типа твердых растворов выше, чем у чистых металлов, являющихся компонентами сплава?

4. Почему металлические сплавы обладают меньшим температурным коэффициентом удельного сопротивления, чем чистые металлы?

5. При каких условиях возникает термоэлектродвижущая сила?

1)

Металлы обладают высокой электрической проводимостью из-за наличии в них большой концентрации электрических зарядов, способных свободно перемещаться.

2)

Электронный газ в металлах находится в вырожденном состоянии. Поэтому концентрация электронов и их средняя энергия практически не зависят от температуры, но с повышением температуры увеличивается амплитуда колебаний атомов в узлах кристаллической решетки, что приводит к более интенсивному рассеянию электронов в процессе их направленного движения. Соответственно уменьшается средняя длина свободного пробега и возрастает удельное сопротивление.

3)

Статистическое распределение атомов разных сортов по узлам кристаллической решётки в сплаве вызывает флуктуации периодического потенциального поля кристалла, что приводит к сильному рассеянию электронов и росту удельного сопротивления.

4)

В сплавах остаточное сопротивление значительно превышает сопротивление связанное с рассеянием электронов на узлах кристаллической решётки. Поэтому металлические сплавы обладают меньшим температурным коэффициентом удельного сопротивления, чем чистые металлы.

5)

Термоэлемент, составленный из двух различных проводников, образующих замкнутую цепь, называют термопарой. При различной температуре контактов в замкнутой цепи возникнет термоэлектрический ток. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появится термоэлектродвижущая сила (термоЭДС).