Главная страница
Навигация по странице:

  • Расчетно-пояснительная записка

    		•

    Обработка Результатов измерений лабораторная. 1 лаба — копия. Обработка результатов измерений


    Скачать 263.83 Kb.
    НазваниеОбработка результатов измерений
    АнкорОбработка Результатов измерений лабораторная
    Дата02.12.2020
    Размер263.83 Kb.
    Формат файлаdocx
    Имя файла1 лаба — копия.docx
    ТипОтчет
    #156272

    ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

    по дисциплине: Метрология и стандартизация в СПЦЗС
    Тема: «Обработка результатов измерений»
    Расчетно-пояснительная записка

    Разработал(а) студент(ка) hhhhhhh

    Подпись, дата Инициалы, фамилия

    Проверил _________________hhhhhhhhhh

    Подпись, дата Инициалы, фамилия

    Члены комиссии ____________________________________

    Подпись, дата Инициалы, фамилия

    _____________________________________

    Подпись, дата Инициалы, фамилия

    Нормоконтролер _____________________________________

    Подпись, дата Инициалы, фамилия
    Защищен(а)____________________ Оценка _____________________________

    дата


    1. Теоретическая часть

    Результаты измерений x, которые соответствуют нормальному закону распределения, приближенно оцениваются математическим ожиданием m по формуле:

    .

    Для оценки среднеквадратического отклонения (СКО) σ используют выражение:

    .

    Иногда, для достижения наглядности, помимо расчётов, строят различные графики. Чаще всего используют полигон, гистограмму и кумулятивную кривую.

    Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основания которых – отрезки, изображающие интервалы вариационного ряда, а вычеты – частоты соответствующих интервалов.

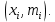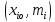    Полигон – ломаная линия, отрезки которой соединяют точки с координатами Для интервального ряда соединяются точки с координатами или .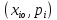

    Кумулятивная кривая – это кривая накопленных частот. Если вариационный ряд дискретный, то кривая представляет собой ломаную линию, отрезки которой соединяют точки с координатам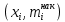и или 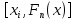. Для интервального вариационного ряда строят ступенчатую кривую. Ширина каждой ступеньки равна величине интервала, а её высота – соответствующему данному интервалу значений накопленной частоты.

    Графическая обработка результатов измерений осуществляется в следующем порядке:

    - строится ранжированный ряд результатов измерений;

    - определяется частота появления i-го результата измерений – mi;

    - вся область изменений величины xi разбивается на k интервалов. Количество интервалов определяется по формуле Старджесса:

    ;

    - ширина интервала определяется по следующей формуле: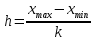

    ;

    - на основании выбранной теоретической функции F(x) определяют вероятность попадания результата измерения в интервал xi-l, xi.

    1. Практическая часть

    Таблица результатов измерений:

    Номер варианта
    Номер эксперимента

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

    8
    136
    139
    135
    136
    133
    136
    135
    137
    136
    139

    9
    137
    135
    136
    140
    138
    137
    136
    137
    135
    135

    0
    138
    137
    137
    139
    137
    138
    132
    138
    134
    137

    Сначала необходимо вычислить математическое ожидание измерений.

    Параметр i = [1 .. 30], n = 30



    Заносим данные о каждом измерении и о разнице полученных значений со средним ожидаемым в таблицу.

    i
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

    xi
    136
    139
    135
    136
    133
    136
    135
    137
    136
    139



    -0.5
    2.5
    -1.5
    -0.5
    -3.5
    -0.5
    -1.5
    0.5
    -0.5
    2.5



    i
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20

    xi
    137
    135
    136
    140
    138
    137
    136
    137
    135
    135



    0.5
    -1.5
    -0.5
    3.5
    1.5
    0.5
    -0.5
    0.5
    -1.5
    -1.5



    i
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30

    xi
    138
    137
    137
    139
    137
    138
    132
    138
    134
    137



    1.5
    0.5
    0.5
    2.5
    0.5
    1.5
    -4.5
    1.5
    -2.5
    0.5

    Расположим результаты в порядке возрастания .

    i
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

    xi
    132
    133
    134
    135
    135
    135
    135
    135
    136
    136



    -4.5
    -3.5
    -2.5
    -1.5
    1.5
    -1.5
    1.5
    -1.5
    -0.5
    -0.5



    i
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20

    xi
    136
    136
    136
    136
    137
    137
    137
    137
    137
    137



    -0.5
    -0.5
    -0.5
    -0.5
    0.5
    0.5
    0.5
    0.5
    0.5
    0.5



    i
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30

    xi
    137
    137
    138
    138
    138
    138
    139
    139
    139
    140



    0.5
    0.5
    1.5
    1.5
    1.5
    1.5
    2.5
    2.5
    2.5
    3.5

    Вычисляем СКО измерений.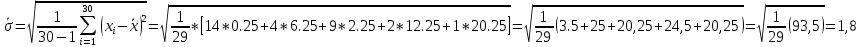

    .

    Определим количество интервалов и границы оных для построения гистограммы.

    Всего имеется n = 30 измерений. xmin = 132, xmax = 140.

    xi
    Количество появлений

    132
    1

    133
    1

    134
    1

    135
    5

    136
    6

    137
    8

    138
    4

    139
    3

    140
    1



    Округлим до ближайшего целого числа. Всего будет 6 интервалов.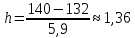



    Округлим и возьмём более удобную ширину интервалов: h = 1.5.
    С шириной h = 1.36 будет неудобно работать, к тому же всего за 6 интервалов она не покроет необходимую область. Получается, что 6 областей будут умещаться в {131,32 - 139,48}. Из-за такого выбора потеряется xi = 140.

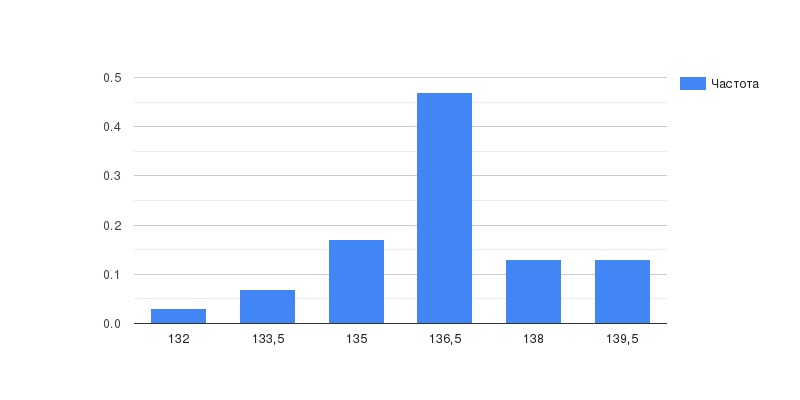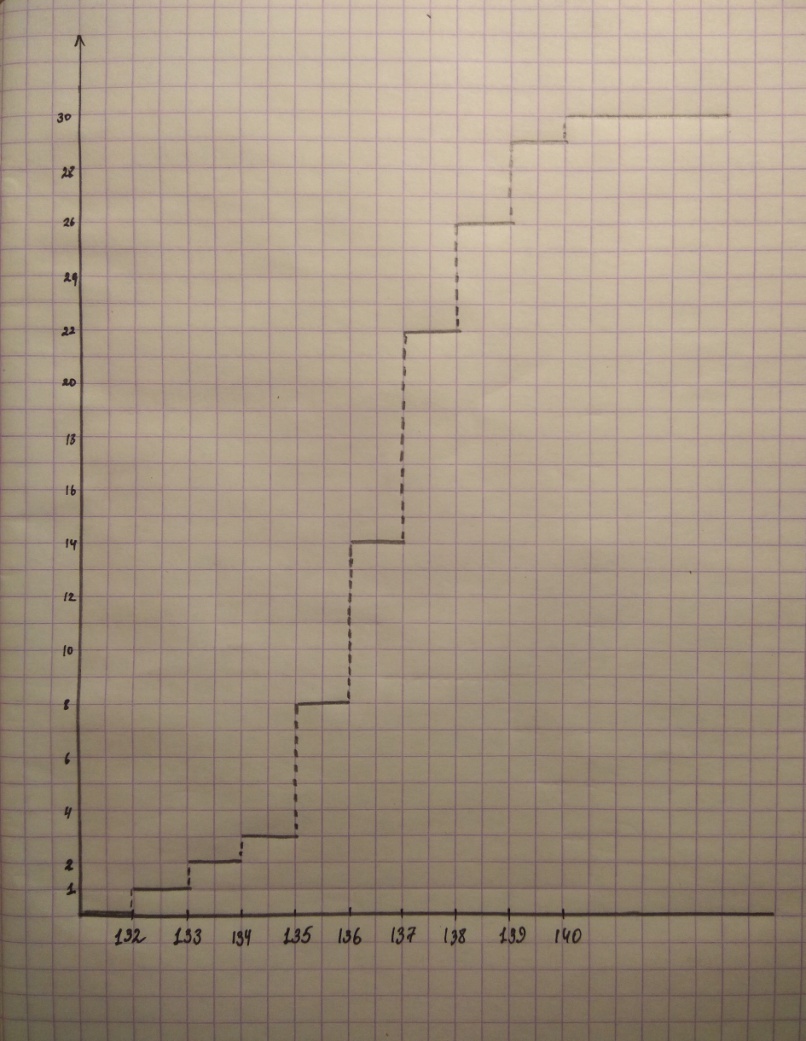    Принцип интервалов xi – xi+1
    Середина интервала xoi
    Частота попадания в интервалы

    mi
    Статистическая вероятность

    pi

    131.25 – 132.75
    132
    1
    0,03

    132.75 – 134.25
    133.5
    2
    0,07

    134.25 – 135.75
    135
    5
    0,17

    135.75 – 137.25
    136.5
    14
    0,47

    137.25 – 138.75
    138
    4
    0,13

    138.75 – 140,25
    139.5
    4
    0,13

    1.00




    написать администратору сайта