Методический материал (1). Обработка результатов прямых многократных измерений Порядок обработки результатов измерений
 Скачать 25.77 Kb. Скачать 25.77 Kb.
|
|
Обработка результатов прямых многократных измерений Порядок обработки результатов измерений: исключить известные систематические погрешности из результатов измерений. определить среднее арифметическое значение 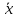 по формуле: по формуле: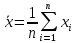 где хi – i-й результат измерения; n – число исправленных результатов измерений. вычислить среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле: 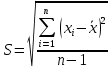 исключить грубые ошибки (промахи), используя критерий Граббса, сравнивая G1 и G2 с теоретическим значением GT при выбранном уровне значимости q. Таблица 1 – Критические значения GT для критерия Граббса
G1 и G2 определить по формулам: 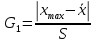 , , 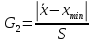 Если G1 > GT, то xmax исключают как маловероятное значение. Если G2 > GT, то xmin исключают как маловероятное значение. Далее вновь вычисляют 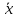 и S и процедуру проверки наличия грубых погрешностей повторяют. и S и процедуру проверки наличия грубых погрешностей повторяют.Если G1 GT, то xmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2 GT, то xmin не считают промахом и его сохраняют в ряду результатов измерений. рассчитать среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) 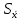 по формуле: по формуле: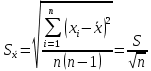 Проверить гипотезу о том, что результаты измерений принадлежат нормальному распределению. При числе результатов измерений 15 < n 50 для проверки принадлежности их к нормальному распределению предпочтителен составной критерий. Считают, что результаты измерений принадлежат нормальному распределению, если не более m разностей 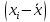 превысили значение превысили значение 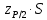 , , где S – среднее квадратическое отклонение, 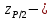 верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности P/2. верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности P/2.Таблица 2 – Значения Р для вычисления 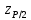
Таблица 3 – Значения 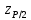
Вычислить доверительные границы случайной погрешности по формуле: 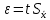 t – коэффициент Стьюдента. Таблица 4 – Значения коэффициента Стьюдента t
Вычислить границы неисключенной систематической погрешности (НСП) Границу НСП 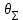 оценки измеряемой величины при наличии менее 3-х (m < 3) НСП, каждая из которых представлена границами оценки измеряемой величины при наличии менее 3-х (m < 3) НСП, каждая из которых представлена границами 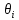 оценивают по формуле: оценивают по формуле: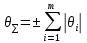 Вычислить доверительные границы погрешности результата измерения по формуле: 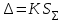 где К – коэффициент зависящий от соотношения случайной составляющей погрешности и НСП; 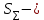 суммарное среднее квадратическое отклонение оценки измеряемой величины, вычисляемое по формуле: суммарное среднее квадратическое отклонение оценки измеряемой величины, вычисляемое по формуле: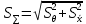 где 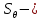 среднее квадратическое отклонение НСП, которое оценивают по формуле: среднее квадратическое отклонение НСП, которое оценивают по формуле: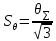 Коэффициент К вычисляют по формуле: 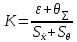 Записать результат измерения При симметричных доверительных границах погрешности результат измерения представляют в форме: 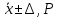 Правила округления при обработке результатов измерений Точность результатов измерений и точность вычислений при обработке результатов измерений должны быть согласованы с требуемой точностью получаемой оценки измеряемой величины. Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами. Число цифр в промежуточных вычислениях при обработке результатов измерений должно быть на две больше, чем в окончательном результате. Погрешность при промежуточных вычислениях должна быть выражена не более чем тремя значащими цифрами. Сохраняемую значащую цифру в погрешности оценки измеряемой величины при округлении увеличивают на единицу, если отбрасываемая цифра неуказываемого младшего разряда больше либо равна пяти, и не изменяют, если она меньше пяти. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
