линал типовые задачи к 2022. Тип.задачи.к.экз.2022 (1). Образцы практических заданий в экз билетах по Лин алг и. анал геом
 Скачать 90.18 Kb. Скачать 90.18 Kb.
|
|
Образцы практических заданий в экз. билетах по «Лин.алг.и.анал.геом» в летнюю сессию 2022. Общие сведения о предстоящем экзамене. В билете под №1 стоит вопрос по теории, который оценивается от 0 до 5 баллов. под №№2-6 стоят задачи, которые оцениваются от 0 до 9 баллов. На экзамен отводится 70 минут. Для положительной оценки следует набрать не менее 15 баллов, при этом две какие-то задачи должны быть решены полностью. Если на экзамене набрано менее 16 баллов, то ставится оценка «неудовлетворительно» и набранные за семестр баллы за активность «сгорают». Если по билету набрано 16 и более баллов, то к набранным баллам прибавляются баллы за активность. В этом случае оценка выставляется по критерию: 16-45 баллов – «удовлетворительно»; 46-60 баллов – «хорошо»; 61-75 баллов – «отлично». Если по билету набрано 50 баллов, то без учета баллов за активность выставляется оценка «отлично». Задачи под №2. Исследование и решение линейных алгебраических уравнений 2.1. Дана система уравнений с параметром 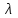 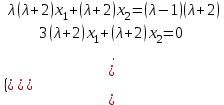 1) При каких значениях параметра 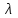 система совместна? система совместна?2) При каких значениях параметра 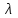 система несовместна? система несовместна?3) При каких значениях параметра 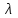 общее решение системы является 0-мерным линейным пространством? общее решение системы является 0-мерным линейным пространством?4) При каких значениях параметра 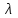 общее решение системы является линейным пространством? общее решение системы является линейным пространством?5) При каких значениях параметра 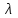 общее решение системы не является линейным пространством? общее решение системы не является линейным пространством?6) При каких значениях параметра 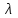 общее решение системы является 0-мерным линейным пространством? общее решение системы является 0-мерным линейным пространством?7) При каких значениях параметра 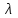 общее решение системы является 1-мерным линейным пространством? общее решение системы является 1-мерным линейным пространством?8) При каких значениях параметра 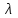 общее решение системы является 2-мерным линейным пространством? общее решение системы является 2-мерным линейным пространством?2.2. Критерием Кронекера-Капелли исследовать систему уравнений на совместность (несовместность). 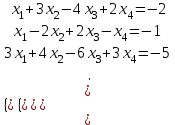 2.3. Найти общее решение неоднородной системы 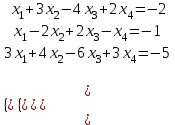 И выделить из него частное решение системы и общее решение соответствующей однородной системы. 2.4. Найти общее решение и ФСР однородной системы 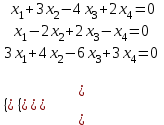 . .Задачи под №3. Матрица перехода от одного базиса к другому. Отображение, оператор, линейный оператор. Матрица линейного оператора. Образ, ядро, ранг, дефект линейного оператора. 3.1. Записать матрицу перехода от базиса 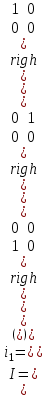 к новому базису к новому базису 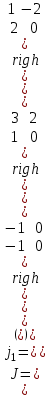 линейного пространства линейного пространства 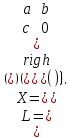 3.2. Записать матрицу перехода от базиса 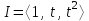 к новому базису к новому базису 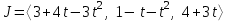 линейного пространства линейного пространства 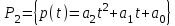 . .3.3. Каким является отображение (оператором или линейным оператором) 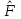 множества множества 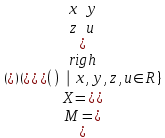 по закону по закону 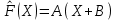 , где , где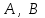 - заданные квадратные матрицы второго порядка? - заданные квадратные матрицы второго порядка?3.4. Доказать, что отображение 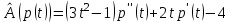 в пространстве многочленов в пространстве многочленов 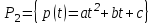 не является линейным оператором. не является линейным оператором. 3.5. Доказать, что отображение 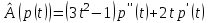 в пространстве многочленов в пространстве многочленов 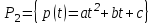 является линейным оператором. является линейным оператором. 3.6. Является ли линейный оператор 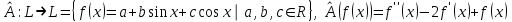 обратимым? обратимым?3.7. Найти образ и ранг (ядро и дефект) линейного оператора 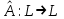 , если , если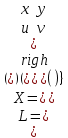 , ,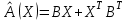 , , 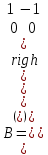 . .3.8. В 3-мерном линейном пространстве 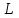 в базисе в базисе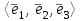 вектор вектор 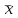 имеет координаты имеет координаты 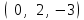 . Найти координаты этого вектора в новом базисе . Найти координаты этого вектора в новом базисе 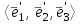 , где , где 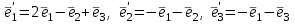 . .Задачи под №4. Собственные числа и собственные векторы. Приведение квадратичной формы к каноническому виду ортогональным преобразованием координат. 4.1. Найдите собственные значения и собственные векторы матрицы 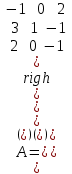 . Будет ли линейный оператор с такой матрицей линейным оператором простого типа? . Будет ли линейный оператор с такой матрицей линейным оператором простого типа?4.2. Найти собственные значения и собственные векторы матрицы 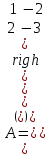 . Будет ли линейный оператор с такой матрицей линейным оператором простого типа? . Будет ли линейный оператор с такой матрицей линейным оператором простого типа?4.3. Линейный оператор простого типа 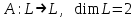 в базисе в базисе 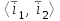 имеет матрицу имеет матрицу 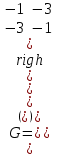 . Найти собственный базис этого оператора. . Найти собственный базис этого оператора.4.4. Найти собственный ортонормированный базис линейного самосопряженного оператора 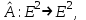 имеющего в ортонормированном базисе имеющего в ортонормированном базисе 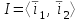 евклидова пространства евклидова пространства 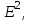 матрицу матрицу 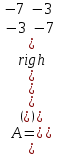 . . 4.5. К какому каноническому виду приводится квадратичная форма 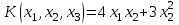 ортогональным преобразованием координат? Найти это преобразование координат. ортогональным преобразованием координат? Найти это преобразование координат.Задачи под №5. Евклидово пространство, скалярное произведение, матрица Грама. Ортогональный и ортонормированный базисы. Метод Грама-Шмидта ортогонализации системы векторов. 5.1. В евклидовом пространстве 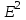 в базисе в базисе 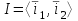 матрица Грама равна матрица Грама равна 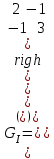 . . 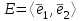 - новый базис, - новый базис,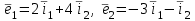 . Записать формулы для скалярного произведения в базисах . Записать формулы для скалярного произведения в базисах 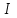 и и 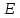 . . 5.2. В двумерном евклидовом пространстве 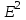 в базисе в базисе 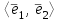 матрица Грама равна матрица Грама равна 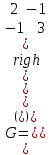 . Найти угол между векторами . Найти угол между векторами 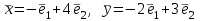 . .5.3. В евклидовом пространстве 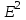 в базисе в базисе 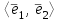 матрица Грама равна матрица Грама равна 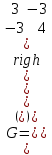 . При каких значениях параметра . При каких значениях параметра 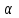 векторы векторы 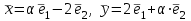 ортогональны. ортогональны.5.4. Какие из приведенных ниже матриц являются матрицами Грама в 3-мерном евклидовом пространстве: 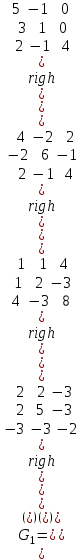 5.5. В евклидовом пространстве 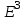 в базисе в базисе 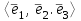 матрица Грама равна матрица Грама равна 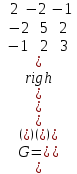 . Вычислить скалярное произведение векторов . Вычислить скалярное произведение векторов 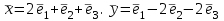 . . Задачи под №6. Билинейные и квадратичные формы. Приведение квадратичных форм методом Лагранжа к каноническому виду. Индексы инерции квадратичной формы. Критерий Сильвестра положительной (отрицательной) определенности квадратичной формы. Ортогональные матрицы, ортогональные преобразования координат. 6.1. Дана билинейная форма 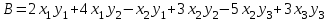 . Найти соответствующую ей квадратичную форму, методом Лагранжа привести ее к каноническому виду, найти индексы инерции, и исследовать на знак квадратичную форму (т.е. является квадр.форма знакопеременной или знакопостоянной со знаком плюс, или знакопостоянной со знаком минус, или положительно определенной, или отрицательно определенной). . Найти соответствующую ей квадратичную форму, методом Лагранжа привести ее к каноническому виду, найти индексы инерции, и исследовать на знак квадратичную форму (т.е. является квадр.форма знакопеременной или знакопостоянной со знаком плюс, или знакопостоянной со знаком минус, или положительно определенной, или отрицательно определенной).6.2. Дана билинейная форма 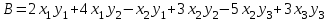 . Найти соответствующую ей квадратичную форму и с помощью критерия Сильвестра исследовать ее на положительную и отрицательную определенность. . Найти соответствующую ей квадратичную форму и с помощью критерия Сильвестра исследовать ее на положительную и отрицательную определенность. 6.3. Проверить, является ли ортогональной матрица 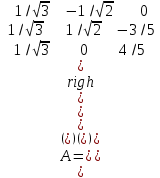 ? ? 6.4. Проверить, будет ли преобразование координат 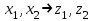 по формулам по формулам 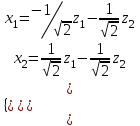 ортогональным? ортогональным? |
