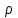Вариант 3. Парная нелинейная регрессия
 Скачать 108.21 Kb. Скачать 108.21 Kb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)»
Институт экономики и финансов Кафедра «Информационные системы цифровой экономики» Расчетно-аналитическая работа №2 по дисциплине: «Эконометрика» на тему: «Парная нелинейная регрессия» Вариант 3 Выполнил: студент(ка) группы _____ _________________________________ _________________________________ Проверил: к.т.н., доцент Ефимов Г.Н. Москва 2022 Для 53 предприятий заданы значения двух признаков Y и X. I. Нелинейная регрессия 1.1. Построить уравнения регрессии: 1.1.1. степенное 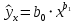 1.1.2. показательное 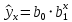 ; ;1.1.3. гиперболическое 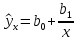 . .1.2. Оценить качество каждого уравнения с помощью средней ошибки аппроксимации; F-критерия Фишера. Найти индексы корреляции, индексы детерминации. Сделать выводы. II. Приложение уравнений парной нелинейной регрессии 2.1. Найти средние и частные коэффициенты эластичности по каждому уравнению регрессии. Сравнить полученные значения. Сделать выводы. III. Сравнение уравнений парной регрессии 3.1. Построить графики линейной (взять из СР_1), степенной, показательной и гиперболической регрессии на одном корреляционном поле. 3.2. Выбрать наилучшее уравнение регрессии из четырех построенных уравнений. I. Нелинейная регрессия 1.1.1. Построим степенное уравнение регрессии вида 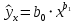
Уравнение степенной регрессии имеет вид: 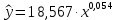 1.1.2. Построим показательное уравнение регрессии вида 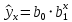
Уравнение показательной регрессии имеет вид: 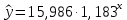 1.1.3. Построим гиперболическое уравнение регрессии вида 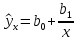
Уравнение гиперболической регрессии имеет вид: 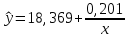 1.2. Оценим качество уравнений регрессии. Найдем средние ошибки аппроксимации по формуле. Для степенной модели: 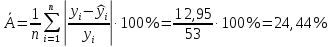 Для показательной модели: 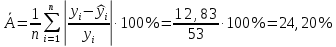 Для гиперболической модели: 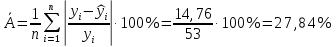 Проверим статистическую значимость уравнений регрессии в целом с помощью F-критерия Фишера. Найдем расчетные значения критерия по формуле: Для степенной модели: 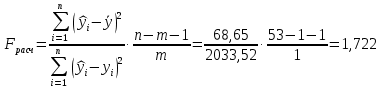 Найдем F-табличное: 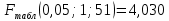 Для показательной модели: 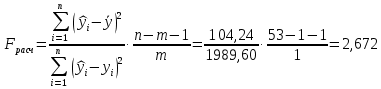 Найдем F-табличное: 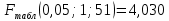 Для гиперболической модели: 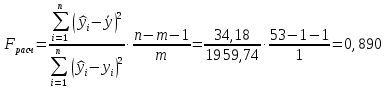 Найдем F-табличное: 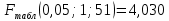 Оценим тесноту нелинейных связей с помощью индекса корреляции, который находится по формуле: Для степенной модели: 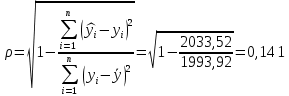 Для показательной модели: 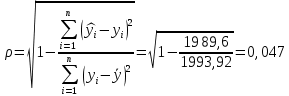 Для гиперболической модели: 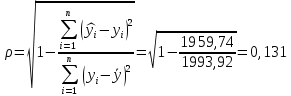 Индексы детерминации найдем по формуле: Для степенной модели: 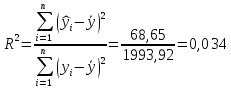 Для показательной модели: 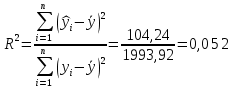 Для гиперболической модели: 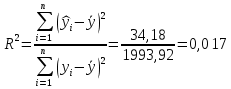 Найдем скорректированные коэффициенты детерминации по формуле: Для степенной модели: 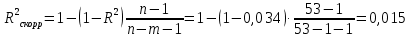 Для показательной модели: 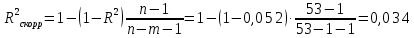 Для гиперболической модели: 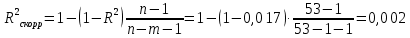 Расчеты характеристик качества уравнений нелинейной регрессии сведем в таблицы. Таблица 1. Оценка качества степенного уравнения регрессии
Вывод: Поскольку 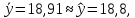 следовательно, расчет параметров произведен верно. следовательно, расчет параметров произведен верно.Таблица 2. Оценка качества показательного уравнения регрессии
Вывод: Поскольку 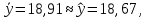 следовательно, расчет параметров произведен верно. следовательно, расчет параметров произведен верно.Таблица 3. Оценка качества гиперболического уравнения регрессии
Вывод: Поскольку 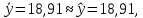 следовательно, расчет параметров произведен верно. следовательно, расчет параметров произведен верно.II. Приложение уравнений парной нелинейной регрессии 2.1. Найдем средние коэффициенты эластичности для нелинейных уравнений регрессии Средний коэффициент эластичности 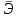 показывает, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора х на 1 % от своего значения. показывает, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора х на 1 % от своего значения.Частный коэффициент эластичности 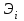 показывает объём изменения результативной переменной у при изменении на 1 % от среднего уровня факторной переменной xi при условии постоянства всех остальных факторных переменных, включённых в модель регрессии. показывает объём изменения результативной переменной у при изменении на 1 % от среднего уровня факторной переменной xi при условии постоянства всех остальных факторных переменных, включённых в модель регрессии. Найдем средние коэффициенты эластичности по каждому уравнению регрессии. Таблица 4
Найдем частные коэффициенты эластичности по каждому уравнению регрессии по формулам Таблица 5
Значения частных коэффициентов эластичности приведены в Приложении. Выводы по частным коэффициентах эластичности степенного уравнения регрессии: Увеличение показателя “Удельный вес покупных изделий” на 1% приводит к увеличению показателя “Производительность труда” на 0,054%. Вывод о частных коэффициентах эластичности показательного уравнения регрессии: Для 50-го наблюдения увеличение показателя “Удельный вес покупных изделий” на 1% приводят к наибольшему увеличению процента “Производительность труда”, чем в целом по группе наблюдений ( 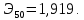 ) (для данных наблюдений влияние x на y наибольшее). Таким образом, в рамках построенной показательной модели для большего значения показателя “Удельный вес покупных изделий” влияние показателя “Производительность труда” наибольшее. ) (для данных наблюдений влияние x на y наибольшее). Таким образом, в рамках построенной показательной модели для большего значения показателя “Удельный вес покупных изделий” влияние показателя “Производительность труда” наибольшее.Для 51-го и 52-го наблюдений увеличение показателя “Удельный вес покупных изделий” на 1% приводит к наименьшему увеличению процента “Производительность труда”, чем в целом по группе наблюдений (Э51=0,060; Э52=0,080). Вывод о частных коэффициентах эластичности гиперболического уравнения регрессии: Анализ значений частных коэффициентов эластичности показывает, что для 14-го и 52-го наблюдений показатель “Удельный вес покупных изделий” имеет наибольшее влияние на показатель “Производительность труда”. (Э14=-0,177; Э52=-0,177). Для 50-го и 43-го наблюдений увеличение показателя “Удельный вес покупных изделий” на 1% приводит к наименьшему увеличению процента “Производительность труда”, чем в целом по группе наблюдений (Э50=-0,007; Э43=-0,008 ). III.Сравнение уравнений парной регрессии 3.1. Построим линейную (взять из СР_1), показательную, степенную и гиперболическую регрессию на одном корреляционном поле. 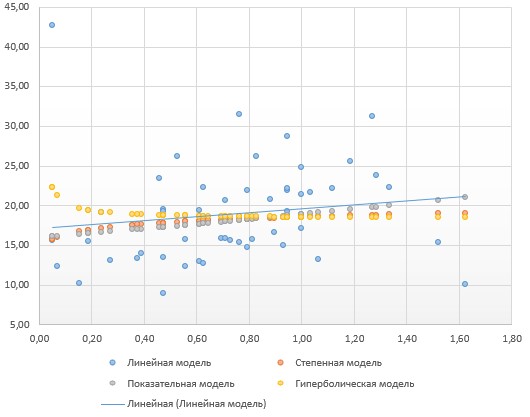 Рисунок. Линии регрессии на корреляционном поле 3.2. Выберем наилучшее уравнение регрессии из четырех построенных уравнений. Для удобства представим имеющиеся данные в табл. 6. Таблица 6. Характеристики парных регрессионных моделей
Вывод: Линейная модель имеет наилучшие значения модельных характеристик: наименьшую среднюю ошибку аппроксимации (наилучшая математическая точность); наибольший индекс корреляции (наиболее сильная нелинейная связь); наибольшее расчетное значение критерия Фишера (наиболее адекватное описание исходных данных). Также на рисунке видно, что линия линейной регрессии проходит внутри корреляционного поля. Кроме того, число точек корреляционного поля, лежащих выше линии регрессии, примерно равно числу точек, лежащих ниже линии регрессии. Следовательно, линия регрессии занимает правильное положение. Для практического применения следует использовать выводы о степени влияния удельного веса покупных изделий на производительность труда, сделанные по коэффициентам эластичности, которые вычислены для линейной модели. Приложение Таблица. Частные коэффициенты эластичности
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

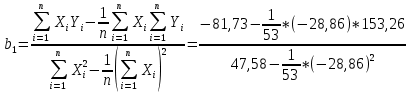
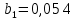
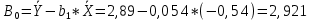
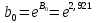
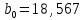
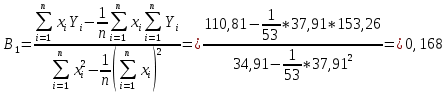
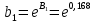
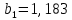
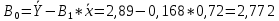
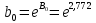
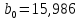
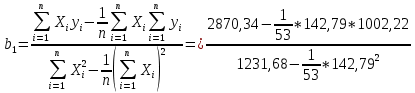
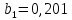
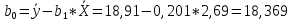
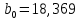
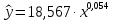
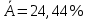
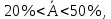 то точность подбора уравнения является удовлетворительной.
то точность подбора уравнения является удовлетворительной.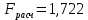
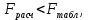 то уравнение степенной регрессии статистически незначимо в целом, т.е. неадекватно описывает исходные данные.
то уравнение степенной регрессии статистически незначимо в целом, т.е. неадекватно описывает исходные данные.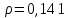
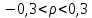 , следовательно, степенная связь между показателями “Удельный вес покупных изделий” и “Производительность труда” слабая или отсутствует.
, следовательно, степенная связь между показателями “Удельный вес покупных изделий” и “Производительность труда” слабая или отсутствует.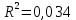
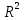 показывает, что в степенной модели формирование значений показателя “Производительность труда” на 3,4% объясняется влиянием показателя “Удельный вес покупных изделий”. Остальные 96,6%
показывает, что в степенной модели формирование значений показателя “Производительность труда” на 3,4% объясняется влиянием показателя “Удельный вес покупных изделий”. Остальные 96,6% 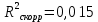
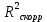 показывает, что в степенной модели формирование значений показателя “Производительность труда” на 1,5% объясняется влиянием показателя “Удельный вес покупных изделий”. Остальные 98,5% приходятся на другие факторы, не включенные в модель.
показывает, что в степенной модели формирование значений показателя “Производительность труда” на 1,5% объясняется влиянием показателя “Удельный вес покупных изделий”. Остальные 98,5% приходятся на другие факторы, не включенные в модель.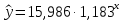
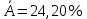
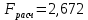
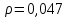
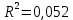
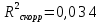
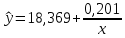
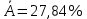
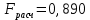
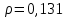
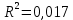
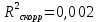
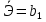
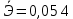
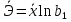
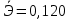
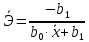
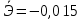
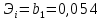
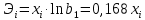
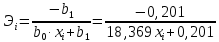
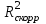
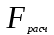
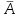 , (%)
, (%)