Образец выполнения лабораторной работы 1
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
Образец выполнения лабораторной работы 1 Дана малая выборка объема n 20 из нормальной генеральной совокупности N(0; 1), записанная в виде таблицы 1. 3Для нее требуется построить статистические характеристики, перечисленные в §2. Таблица 1. Выборка объема n 20 из распределения N(0; 1).  Строим вариационный ряд и записываем его в виде таблицы 1.4.
Таблица 1.4. Вариационный ряд для выборки из таблицы 1.3.  Дана большая выборка объема n 100 элементов из нормальной генеральной совокупности N(0; 1), записанная в виде таблицы 1.5, причем малая выборка (таблица 1.3) является ее частью. Требуется построить статистические характеристики, перечисленные в п.п. 2.11–2.15, а также графики функций (x) и (x) (п.п. 2.16, 2.17). Таблица 1.5. Большая выборка объемом n 100 элементов из нормальной генеральной совокупности N. 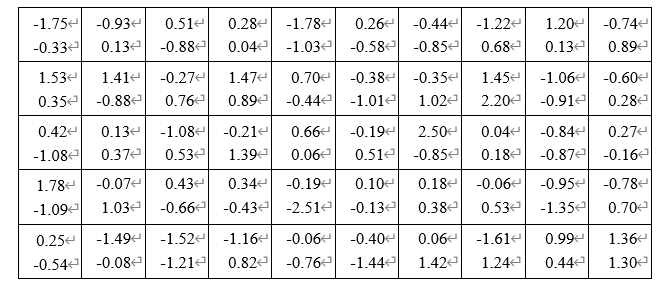 Образуем группированный статистический ряд.  Распределяем элементы выборки по образованным промежуткам 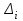 и подсчитываем частоты и подсчитываем частоты 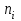 (i 1, , 8). Технически это делается следующим образом. Просматриваем выборку по порядку и каждый элемент относим в соответствующий промежуток, ставя при этом палочку в графе (таблица 1.6) рядом. Когда накапливается четыре палочки ||||, их перечеркиваем после появления в этом промежутке следующего элемента. Получается пяток (i 1, , 8). Технически это делается следующим образом. Просматриваем выборку по порядку и каждый элемент относим в соответствующий промежуток, ставя при этом палочку в графе (таблица 1.6) рядом. Когда накапливается четыре палочки ||||, их перечеркиваем после появления в этом промежутке следующего элемента. Получается пяток 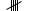 . Затем образуем следующий пяток и т.д. . Затем образуем следующий пяток и т.д.Все результаты, составляющие группированный статистический ряд оформляем в виде таблицы 1.6. Таблица 1.6. Группированный статистический ряд для выборки объемом n100 элементов из таблицы 1.5. 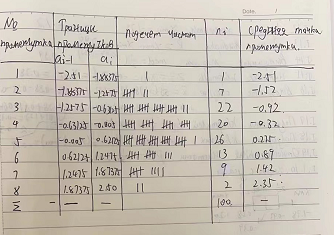 Строим гистограмму приведенных частот (рис.1.1), полигон, кривую Гаусса на одном чертеже для взаимного сравнения. Строим кумуляту и график функции Лапласа на одном чертеже для взаимного сравнения (рис.1.2). Предварительно составляем аналитическое выражение для эмпирической функции распределения: 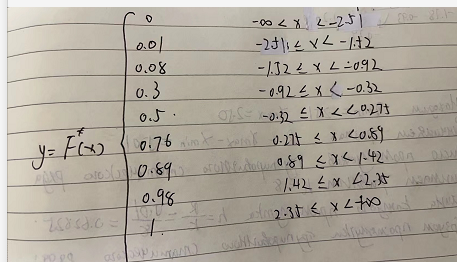 С помощью таблицы 1.5 вычисляем относительную частоту события X 0: P(b)=50/100=1/2=0.5  Рис. 1.1. Гистограмма приведенных частот, полигон, кривая Гаусса. 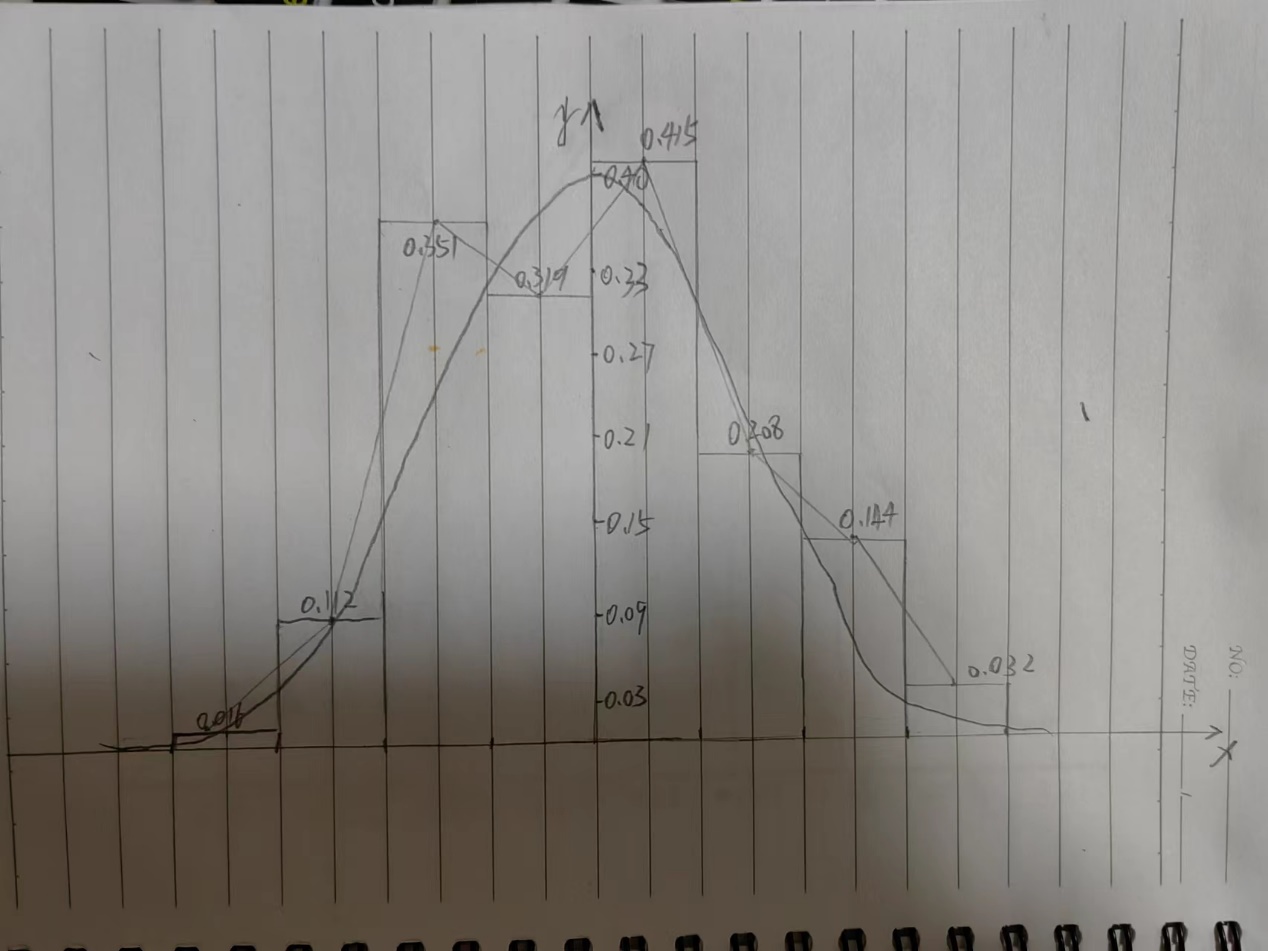 Рис. 1.2. Кумулята и график функции Лапласа. 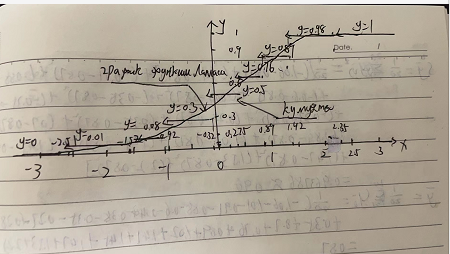 §6. Выводы Выборочные характеристики положения малой выборки; Среднее значение x=-0.32,med 0.39,t(q)=-0.33;t(R)=-0.29, не являются взаимно близкими в силу наличия аномального для малой выборки Минимальное значение x=-1.78, не уравновешенного слева. Ближе всего к истинному центру симметрии x 0 находится медиана, дальше всего –tq Ящик с усами показывает, что центр распределения близок к точке x 0. Крайние элементы 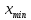 =-2.51 и =-2.51 и 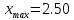 располагаются несимметрично относительно центра. Степень концентрации элементов выборки к центру – высокая. Между квартилями находятся 12 элементов вместо половины. располагаются несимметрично относительно центра. Степень концентрации элементов выборки к центру – высокая. Между квартилями находятся 12 элементов вместо половины.График выборочных распределений – гистограмма – ступенчатая линия, полигон, кумулята хорошо аппроксимирует теоретические кривые – Гаусса и Лапласа, поэтому можно выдвинуть гипотезу о нормальности генерального распределения. Относительные частоты 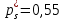 , , 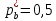 в сравнении с истинной вероятностью P(X 0) 0,5 свидетельствуют в пользу симметричности генерального распределения. в сравнении с истинной вероятностью P(X 0) 0,5 свидетельствуют в пользу симметричности генерального распределения. |
