 y y
 1 1
-1 1 x
-1
11.13. Система случайных величин (X, Y) подчинена закону распределения с плотностью:
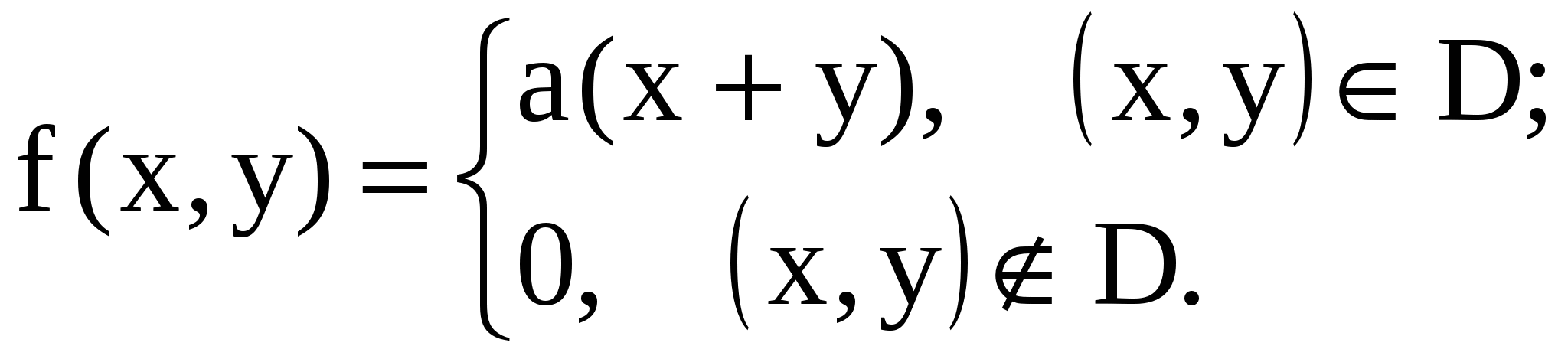
Область D - квадрат, ограниченный линиями x = 0; x = 3; y = 0; y = 3.
Найти: а) Коэффициент a; б) вероятность попадания случайной точки (x, y) в квадрат, ограниченный прямыми x = 1, x = 2, y = 1, y = 2; в) 
11.14. Определить плотность распределения вероятностей, математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если  , , 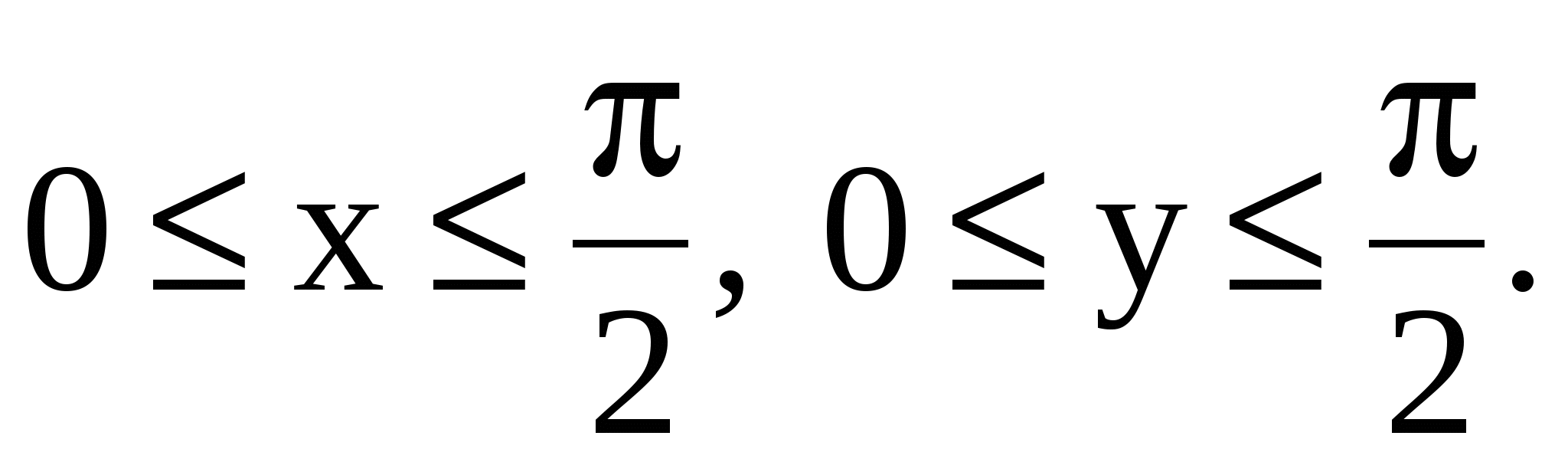
11.15. Плотность совместного распределения случайных величин (X,Y): 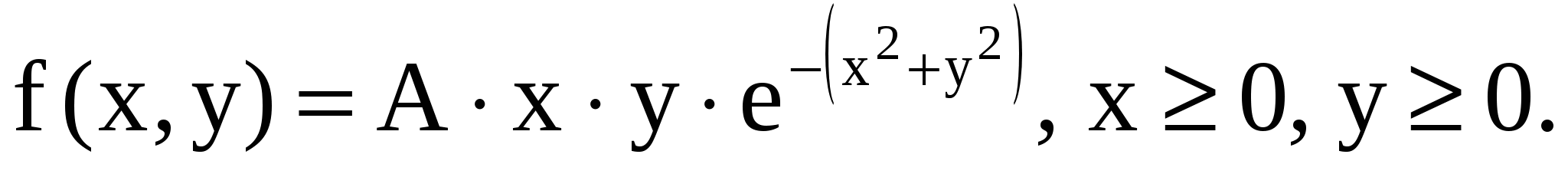 Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес- Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
кие ожидания каждой из случайных величин.
11.16. Плотность совместного распределения системы случайных величин X, Y равна 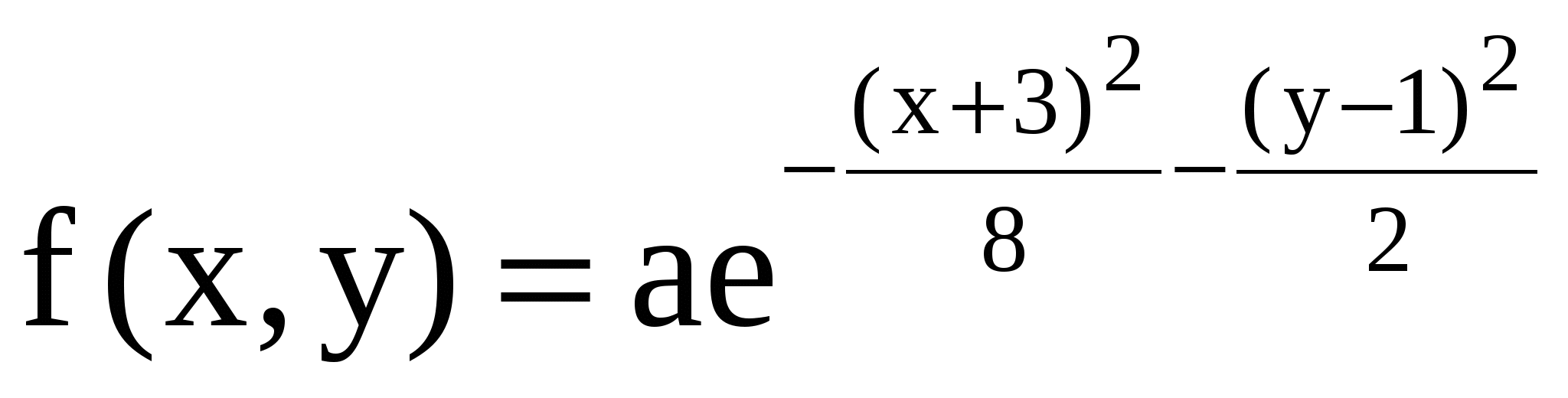 . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4. . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
11.17. Координаты случайной точки (X,Y) раcпределены равномерно внутри прямоугольника, ограниченного прямыми x = 0, x = a, y = 0, y = b. Определить вероятность попадания случайной точки в круг радиуса R = a ,если a > b, а центр круга совпадает с началом координат.
11.18. Координаты (X, Y) случайной точки распределены равномерно внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c , y = d (в > a , d > c). Найти плотность распределения вероятностей и функцию распределения системы случайных величин X, Y. Выяснить, являются ли X, Y независимыми величинами.
11.19. Плотность совместного распределения случайных величин X, Y равна:
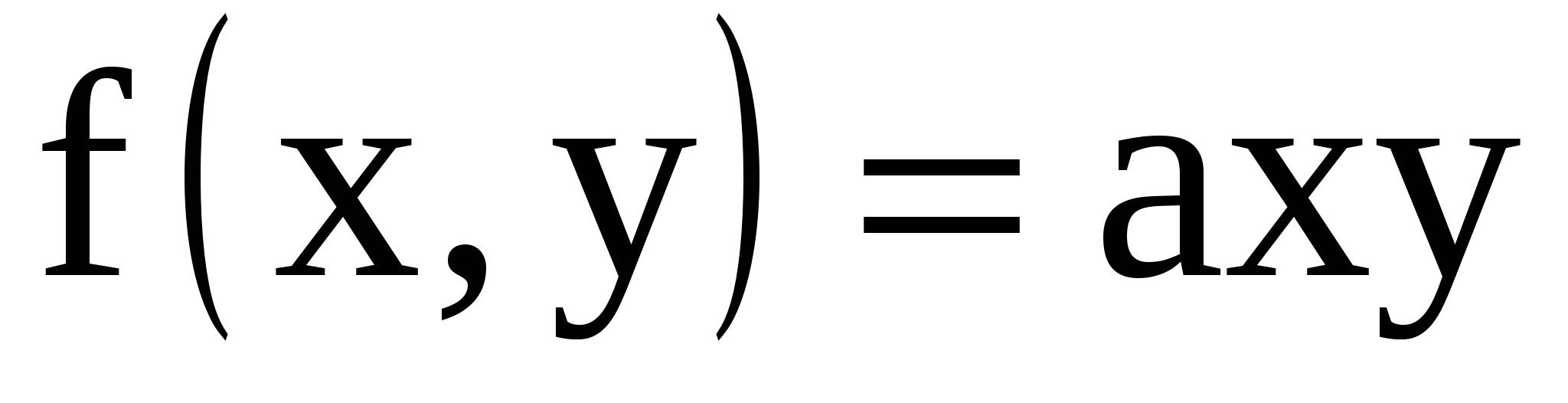 в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми  Найти а) Найти а) 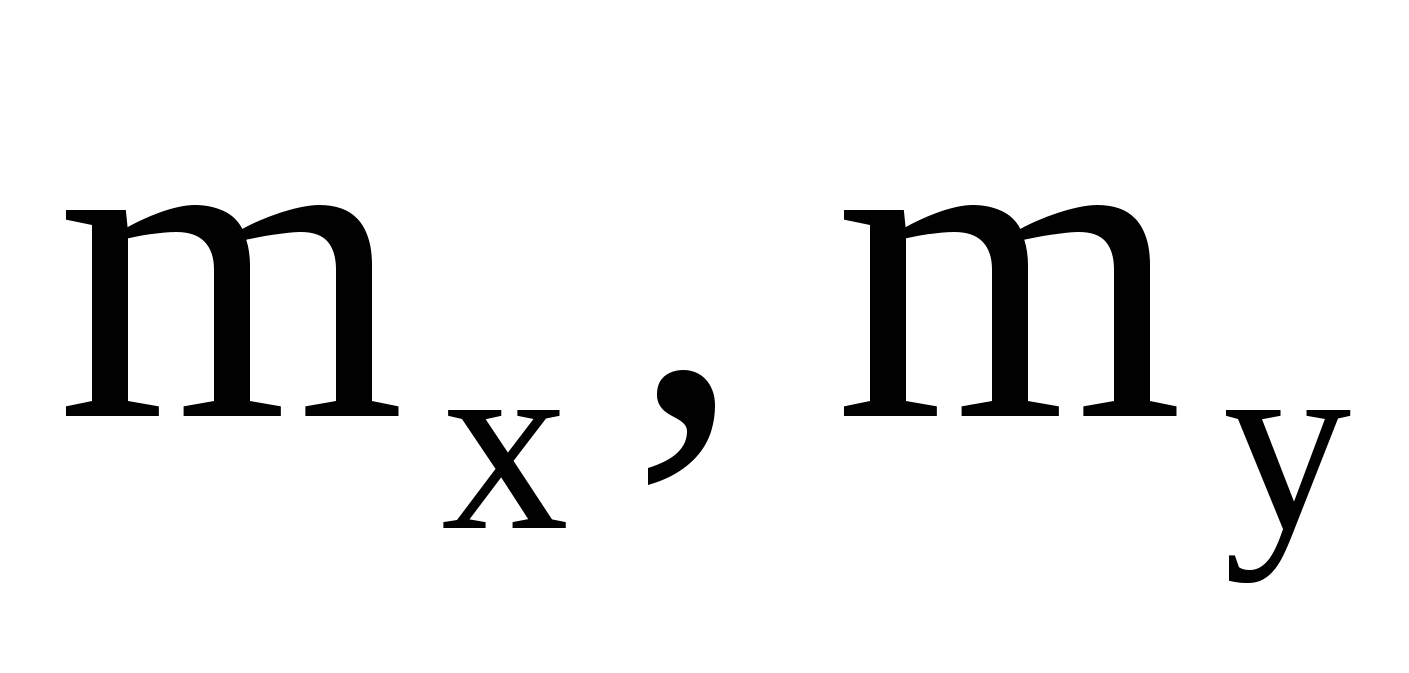 ; б) коэффициент корреляции ; б) коэффициент корреляции 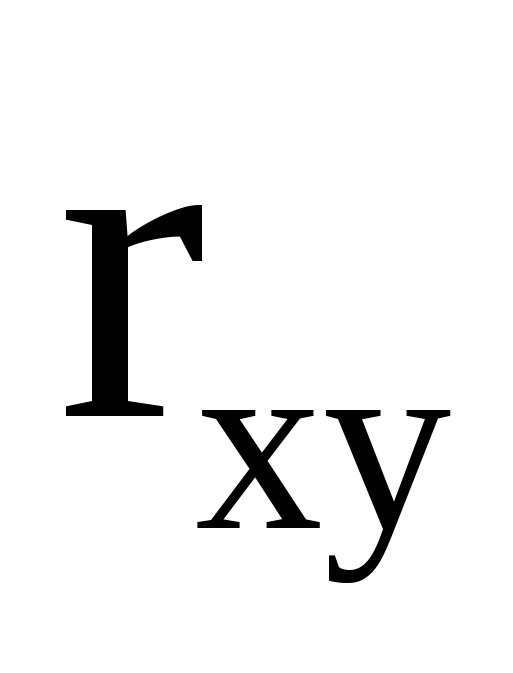 , дисперсии , дисперсии 
11.20. Плотность совместного распределения системы случайные величины
(X, Y), заданной внутри круга радиуса R , равна 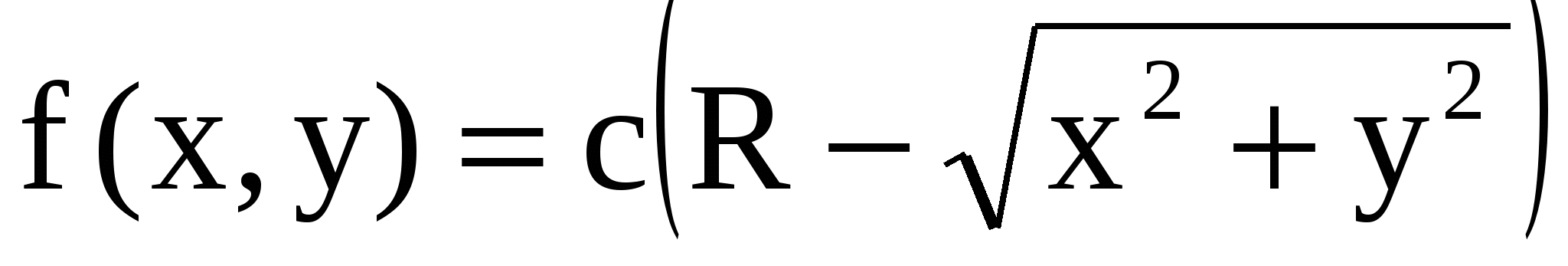 . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат. . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
11.21. Плотность совместного распределения системы случайных величин
(X, Y):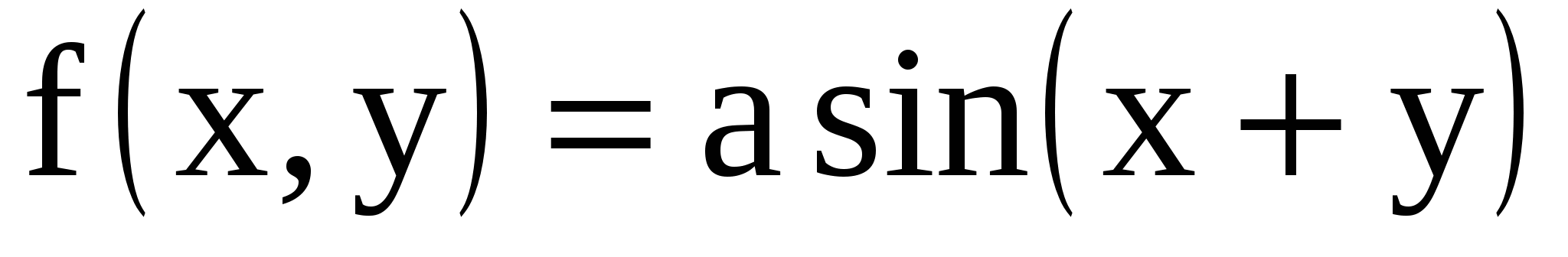 в области D и в области D и 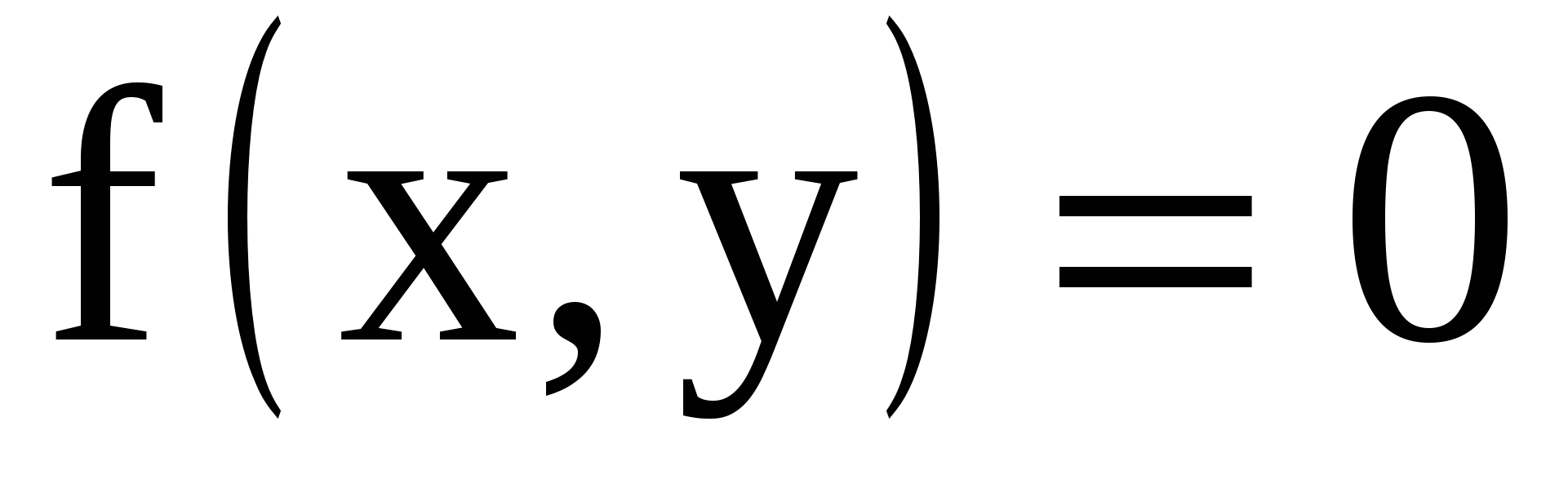 вне этой области. Область D определяется неравенствами вне этой области. Область D определяется неравенствами 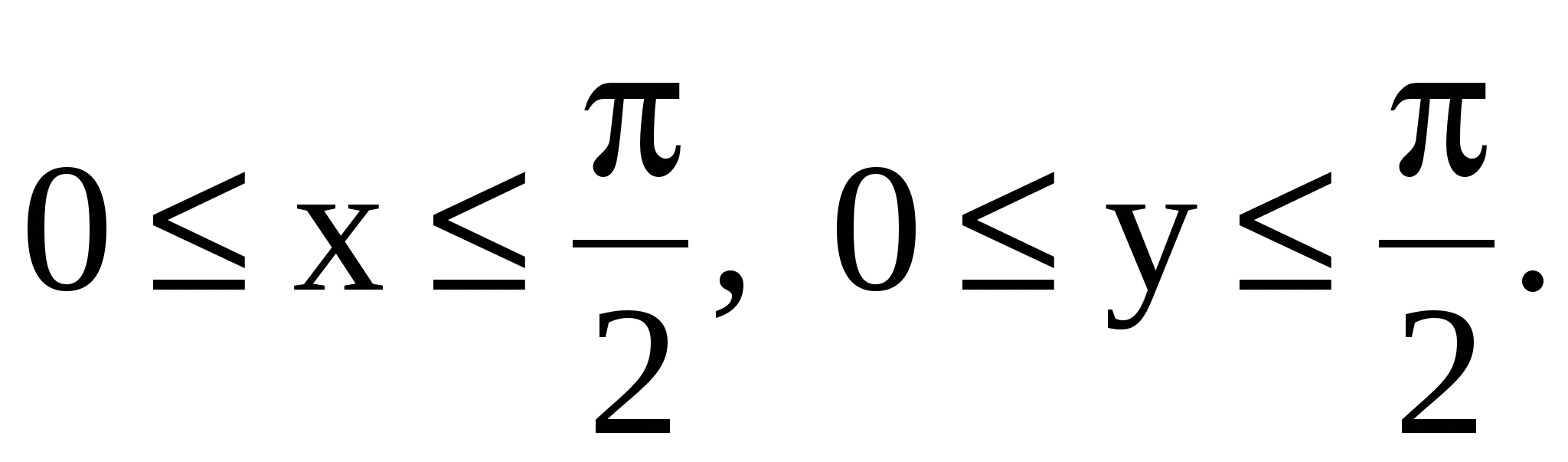 Определить: a) постоянную a; Определить: a) постоянную a;
б) 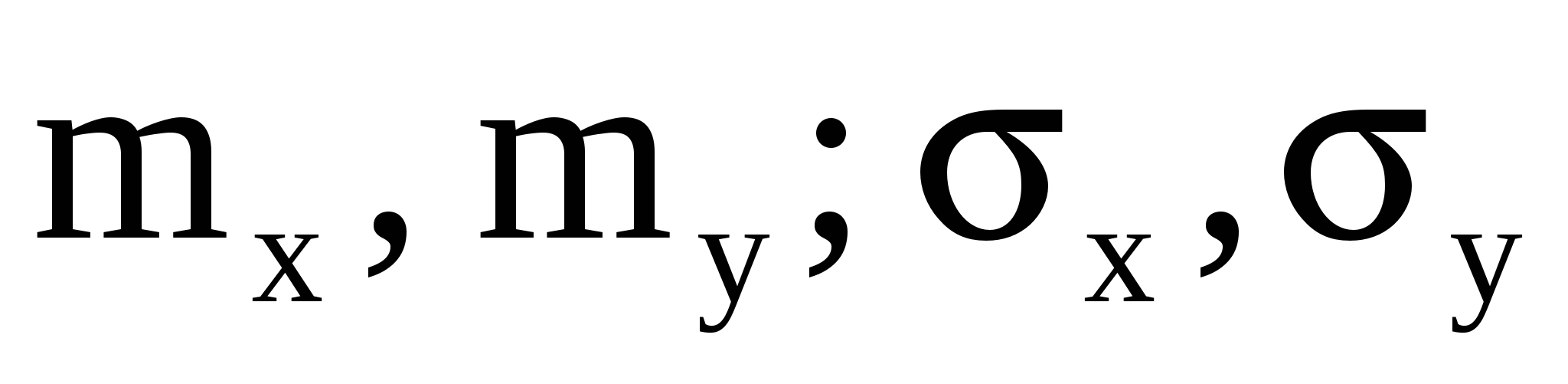 ; в) определить коэффициент корреляции r xy. ; в) определить коэффициент корреляции r xy.
11.22. Дана плотность совместного распределения системы случайных величин 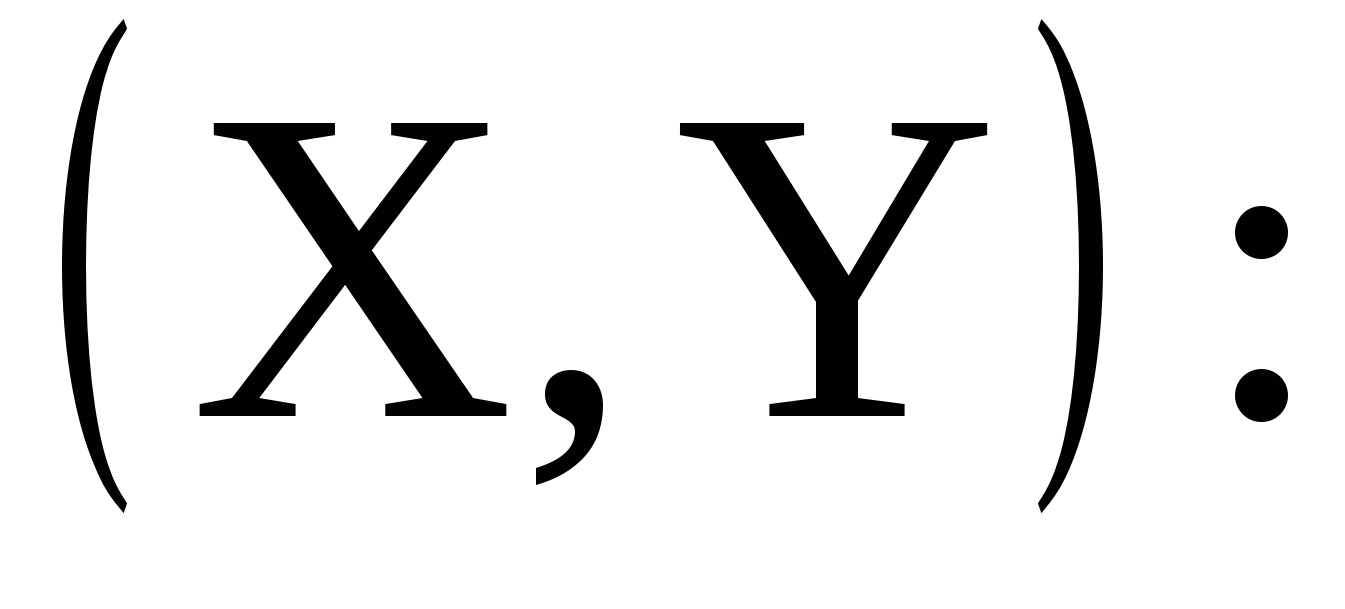  . Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1). . Определить вероятность попадания случайной точки (x, y) в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
11.23. Плотность распределения вероятностей двумерного случайного вектора (X, Y)имеет следующий вид:  . .
Вычислить: а) значение постоянной c; б) вероятность  ); в) центр рассеивания. ); в) центр рассеивания.
11.24. Случайные величины X и Y независимы и распределены каждая по показательному закону с параметрами соответственно 1 и 2. Найти вероятность 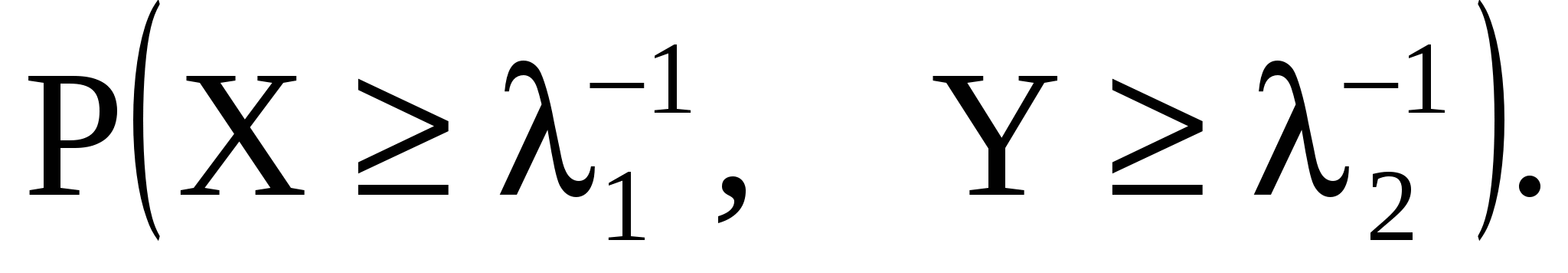
11.25. Функция совместного распределения двух случайных величин X и Y имеет следующий вид:
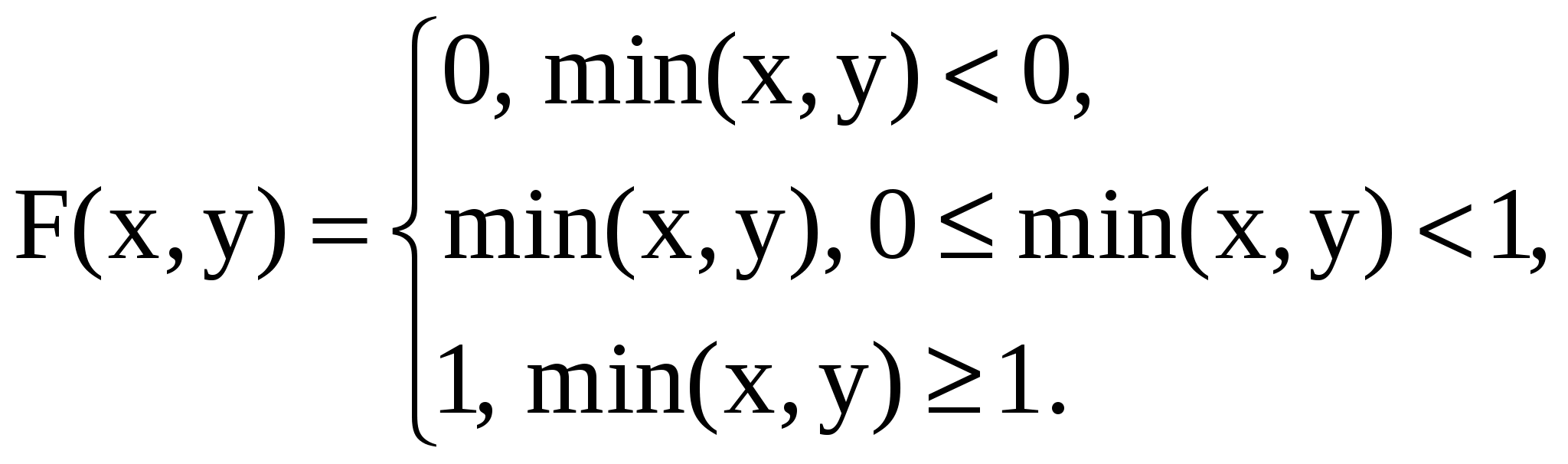
Найти одномерные законы распределения компонент и решить вопрос об их зависимости или независимости.
11.26. Случайные величины X и Y независимы и распределены следующим образом: X - по закону N(1; 2), Y - по равномерному закону на отрезке [0; 2].
Найти вероятность следующих событий:  , где область , где область
D = {(x,y) / (0 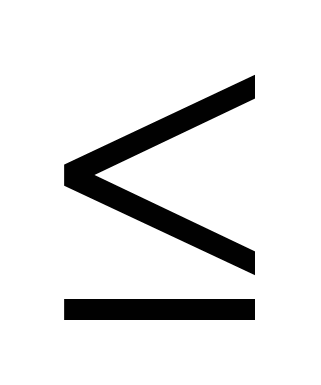 x x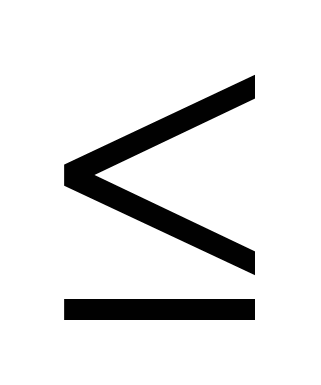 2, 0 2, 0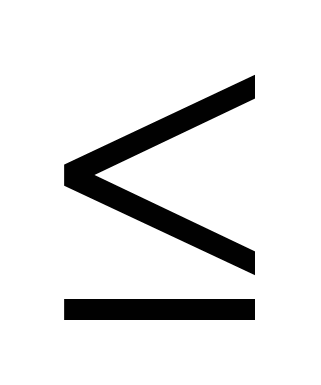 y y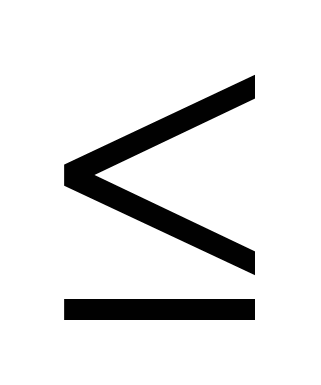 1); B = {X > Y}. 1); B = {X > Y}.
11.27. Случайная точка на плотности (X,Y) распределена по круговому нормальному закону (rxy = 0, x = y = = 1,) с центром рассеивания в начале координат. Вычислить вероятности следующих событий: A = {Y > X},
B = {Y> X}, C = {Y < 3X}, D = {X < 1}, E = {X < 1, Y < 2}.
11.28. Заданы следующие характеристики двумерного нормального вектора:
mx = -2; my = 3 и ковариационная матрица  . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y. . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2x, b = 2y.
11.29. Определить вероятность попадания точки с координатами (X, Y) в область, определяемую неравенствами (1 X 2, 1 Y 2), если функция распреде-ления 
11.30. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения вероятностей 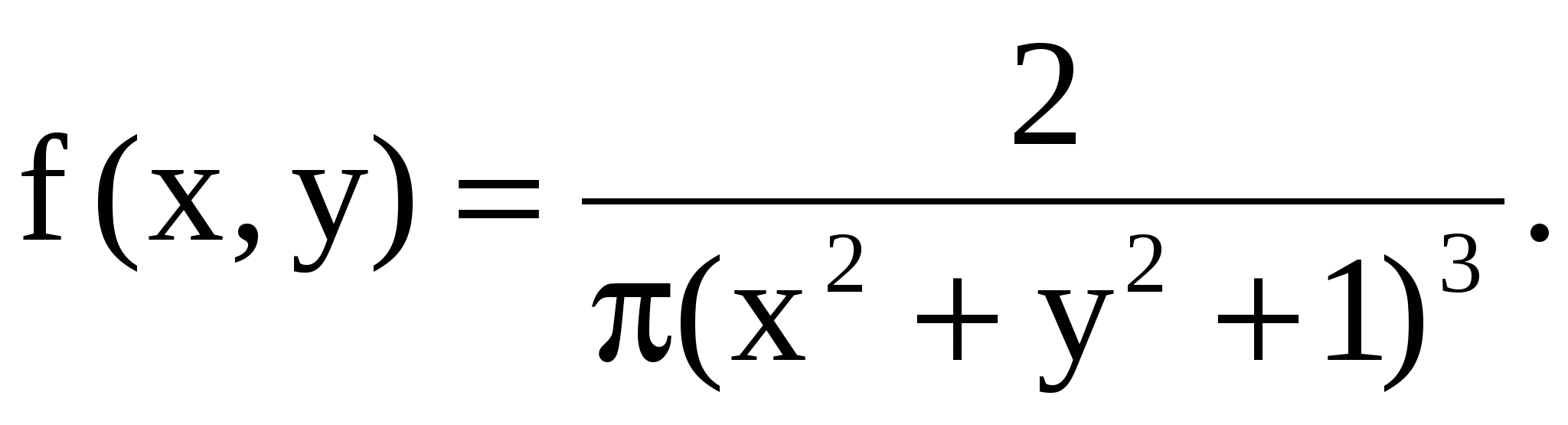
|
 Скачать 0.87 Mb.
Скачать 0.87 Mb.