3. Случайные величины. Образец выполнения заданий
 Скачать 0.87 Mb.
|
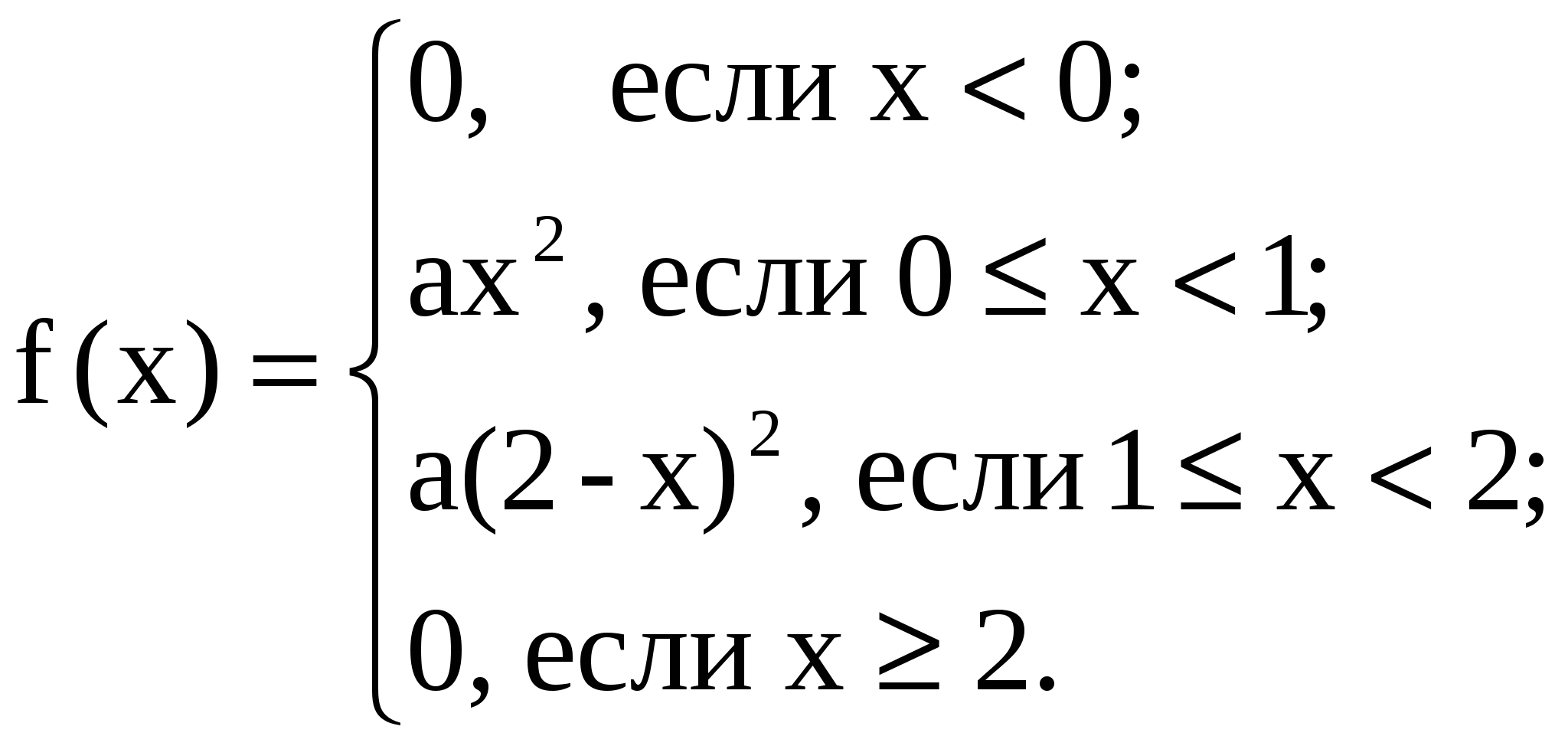 , . Случайная величина  может принимать только одно значение: два с вероятностью, равной единице  .  2  1Задача 7. Дана функция  При каком значении  функция  является плотностью распределения случайной величины  Найти функцию распределения случайной величины  .Решение. Из основного свойства плотности следует   .Для  .Для  .Для   .Для   .Таким образом, 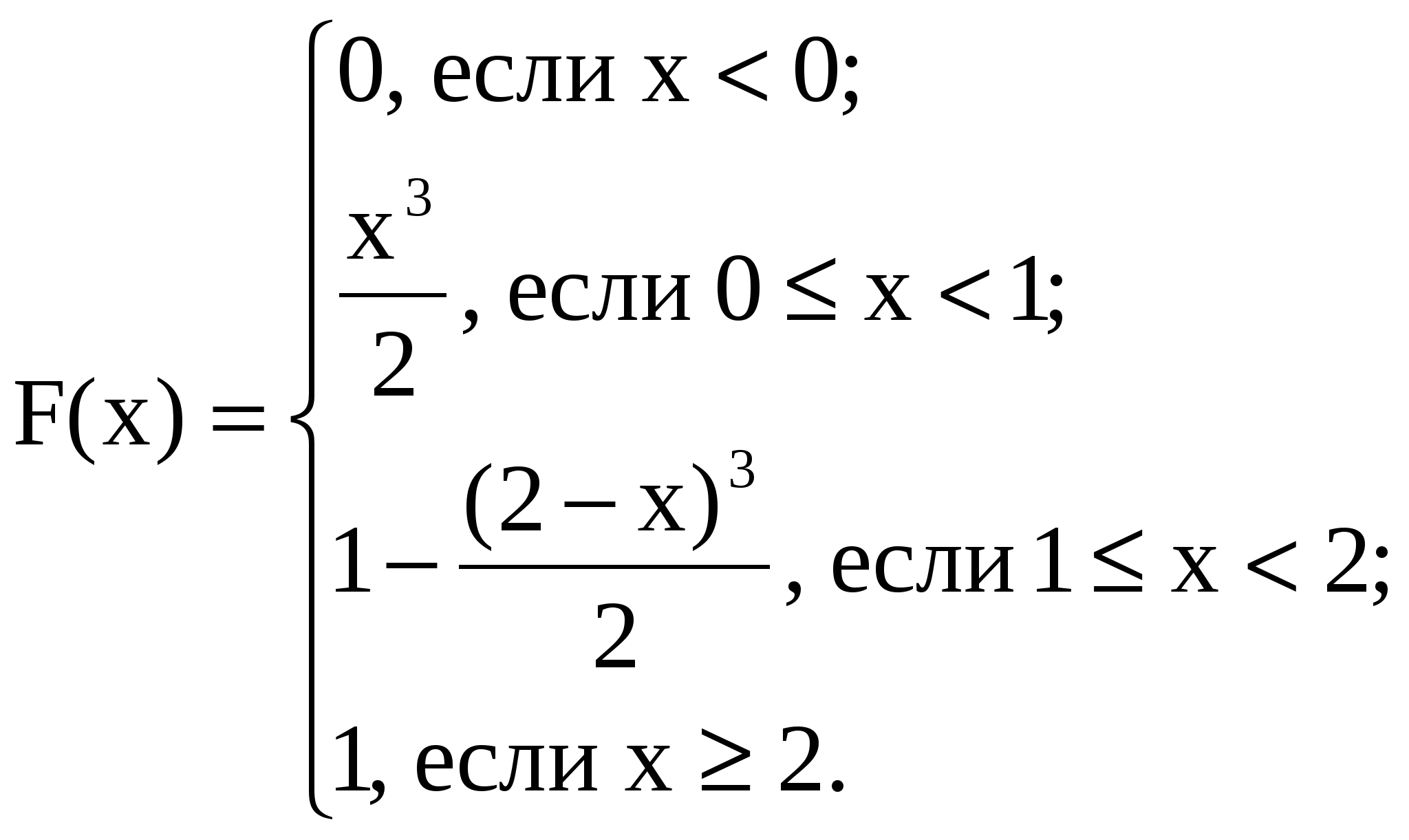 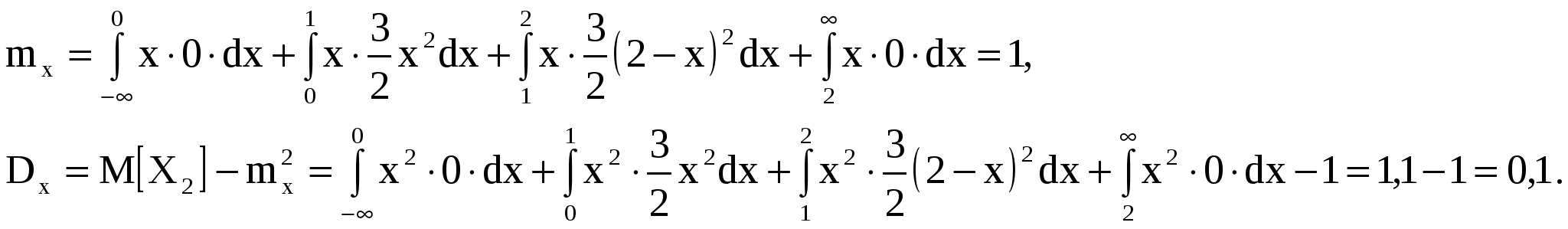 Задача 8. Время Tмежду двумя сбоями ЭВМ распределено по показательному закону с параметром  :  при  . Решение определенной задачи требует безотказной работы машины в течение времени  . Если за время произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время после начала решения задачи. Рассматривается случайная величина  - время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи).Решение. Случайная величина может принимать следующие значения: ( за время не произошло сбоя), 2 (на первом промежутке сбой произошел, на ТОром промежутке сбоя не было), 3 (на первых двух промежутках длины сбои происходили, на третьем сбоя не было) и т. Д.  .Обозначим  тогда  - вероятность того, что за время сбой произошел;  ,  и т. Д. Ряд распределения случайной величины   Х 2 …  …  …  … (вычисление суммы ряда  смотри методические указания к проведению практических занятий по теории вероятностей, часть 2, стр. 15).Задача 9. Известно, что детали, выпускаемые по размерам диаметра, распре-деляются по нормальному закону. Параметры этого закона  ,  . Найти вероятность того, что диаметр наудачу взятой детали имеет размеры в пределах от 4 до 7 см.Решение.  где - математическое ожидание,  - среднее квадратическое отклонение. Таким образом,  Х/Y 20 40 60 10   020   30   Задача 10. Закон распределения системы дискретных случайных величин   задан таблицей: Найти: а) ; б) частные законы распределения случайных величин  ;в)  ,  ; г) коэффициент корреляции  ; д) вероятность попаданий двумерной случайной величины в область  ;  .Решение: так как  то  .Закон распределения случайной величины X   Х 10 20 30Р   , т. К.  .Закон распределения случайной величины Y   Y 20 40 60P   .Отсюда: 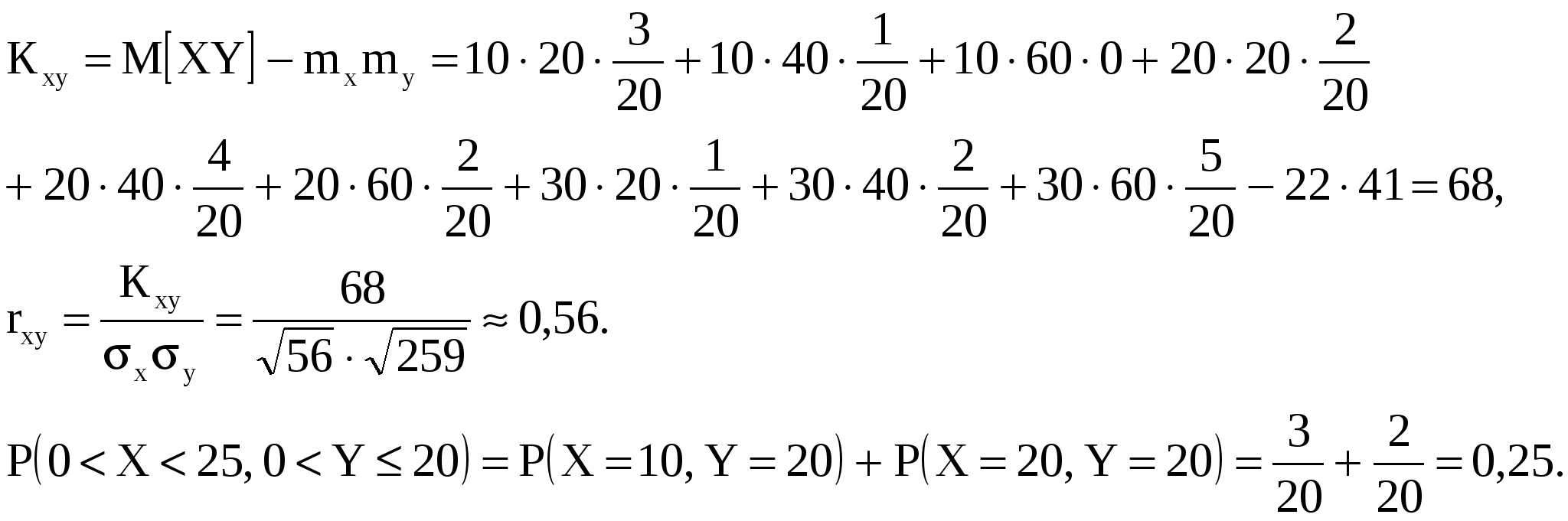  Задача 11. Плотность совместного распределения системы двух случайных величин  задана выражением  . Найти: а) коэффициент А; б) плотности распределения случайных величин , входящих в систему; в) определить зависимы или независимы случайные величины.Решение. Из основного свойства плотности 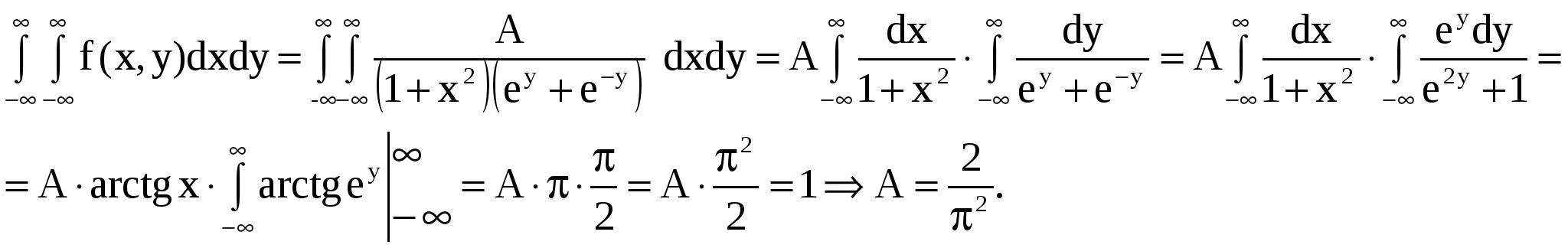 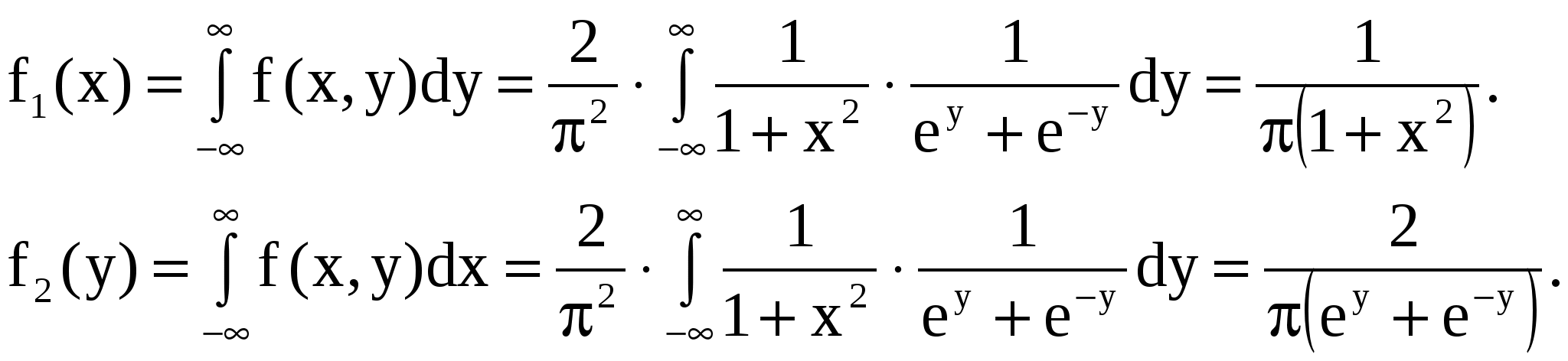 Т.к.  случайные величины - независимы.КОНТРОЛЬНЫЕ ЗАДАНИЯ Задача № 6. 6.1. Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения:  с вероятностью Р1 = 0,1 и  , причем  . Математическое ожидание М[X] = 5,8, дисперсия D[X] = 0,36.6.2. Найти математическое ожидание суммы очков, выпадающих на двух игральных кубиках при одном бросании. 6.3. Случайная величина X - число попаданий мяча в корзину при одном броске. Вероятность попадания равна 0,3. Найти математическое ожидание этой случайной величины, дисперсию, второй начальный момент и третий центральный момент. 6.4. Производится ряд выстрелов по мишени с вероятностью попадания 0,8 при каждом выстреле, стрельба ведется до первого попадания в мишень, но не свыше четырех выстрелов. Найти закон распределения, математическое ожидание и дисперсию числа произведенных выстрелов. Построить функцию распределения, определить вероятность того, что число выстрелов до первого попадания будет не менее трех. 6.5. Дан перечень возможных значений дискретной случайной величины X:  , а также даны математические ожидания этой случайной величины и ее квадрата  . Найти вероятности P1, P2, P3, соответствующие возможным значениям  .6.6. Известно, что в партии из 20 телефонных аппаратов имеется 5 неисправных. Из партии выбрано 4 аппарата. Найти закон распределения, математическое ожидание и дисперсию числа неисправных аппаратов среди отобранных. Построить функцию распределения. Определить вероятность того, что число неисправных аппаратов среди отобранных будет не более двух. 6.7. Вероятность изготовления нестандартного изделия при налаженном технологическом процессе постоянна и равна 0,1. Для проверки качества изготовляемых изделий отдел технического контроля берет из партии не более 4-х деталей. При обнаружении нестандартного изделия вся партия задерживается. Составить закон распределения числа изделий, проверяемых из каждой партии. Найти математическое ожидание, среднее квадратическое отклонение этой случайной величины. 6.8. Случайная величина Х распределена по следующему закону:
|