§ 5.3. Сравнение эффективности проточных реакторов
идеального смешения и идеального вытеснения
Как видно из примеров 5.1 и 5.2, при одинаковых условиях проведения одной и той же реакции для достижения равной глубины превращения среднее время пребывания реагентов в проточном реакторе идеального смешения больше, чем в реакторе идеального вытеснения. Этот факт легко может быть объяснен характером распределения концентрации реагентов по объему указанных реакторов. Если в проточном реакторе идеального смешения концентрации во всех точках равны конечной концентрации (рис. 5.6, линия 1), то в реакторе идеального выяснения в двух соседних точках на оси реактора концентрации реагентов уже отличаются (линия 2). Например, в соответствии с уравнением (5.12) в случае реакции первого порядка (wrA = kсА)формула распределения концентрации реагента А по длине реактора идеального вытеснения имеет вид
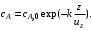
Скорость реакции, согласно закону действующих масс, пропорциональна концентрации реагентов. Следовательно, в реакторе идеального вытеснения она всегда выше, чем в проточном реакторе идеального смешения. А при большей скорости протекания реакции для достижения той же глубины превращения требуется меньшее время пребывания реагентов в реакторе.
Более наглядно эти положения можно проиллюстрировать, сравнивая среднее время пребывания реагентов в проточных реакторах как площади геометрических фигур.
Сравним эффективность работы идеальных проточных реакторов для случая проведения в них простых реакций, не осложненных побочными взаимодействиями. Зададимся одинаковой степенью превращения исходного реагента, и будем считать более эффективным тот реактор, в котором для достижения заданных результатов требуется меньшее среднее время пребывания 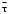 = V/v. = V/v.
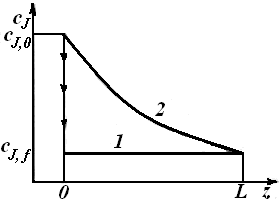
Рис. 5.6. Распределение вдоль оси реактора
концентрации исходного реагента в проточных реакторах
идеального смешения (1) и идеального вытеснения (2)
Для проточного реактора идеального смешения при заданной глубине превращения (концентрации исходного реагента А в выходном потоке сА,f или соответствующей степени превращения хА,f)среднее время пребывания τ в соответствии с уравнениями (5.5) и (5.7) можно определить как произведение двух постоянных величин:
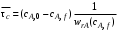
или
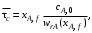
т. е. геометрически представить в виде прямоугольника с соответствующими сторонами.
Для стационарного реактора идеального вытеснения
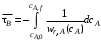
или
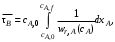
т. е. величина  B как определенный интеграл выражается геометрически площадью криволинейной трапеции, ограниченной прямыми cA = cA,f,cA = cA,0, графиком функции l/wrA= f(cA) и осью абсцисс (см. рис. 5.7, а).Или в соответствии с уравнением (5.7), площадью криволинейной трапеции, ограниченной прямыми хА = 0, хА = xA,fграфиком функции l/wrA = f(хА) и осью абсцисс (см. рис. 5.7, б). B как определенный интеграл выражается геометрически площадью криволинейной трапеции, ограниченной прямыми cA = cA,f,cA = cA,0, графиком функции l/wrA= f(cA) и осью абсцисс (см. рис. 5.7, а).Или в соответствии с уравнением (5.7), площадью криволинейной трапеции, ограниченной прямыми хА = 0, хА = xA,fграфиком функции l/wrA = f(хА) и осью абсцисс (см. рис. 5.7, б).
Из рис. 5.7 видно, что площади криволинейных трапеций, соответствующие  B, меньше площадей прямоугольников, соответствующих B, меньше площадей прямоугольников, соответствующих  С, причем разница тем больше, чем больше достигаемая в реакторе степень превращения исходного реагента. Следовательно, при равном объемном расходе для достижения одинаковых результатов реактор идеального вытеснения должен иметь меньший объем, чем проточный реактор идеального смешения. Интенсивность реактора идеального вытеснения (1 = П / У =vcA,0xA/V)будет выше. Объяснить это можно более высокой скоростью реакции в реакторе вытеснения вследствие более высокой концентрации реагентов, одинаковых результатов. Реактор идеального вытеснения должен иметь меньший объем, чем проточный реактор идеального смешения. Интенсивность реактора идеального вытеснения (1 = П / У = ucA,0xA/V)будет выше. Объяснить это можно более высокой скоростью реакции в реакторе вытеснения вследствие более высокой концентрации реагентов. С, причем разница тем больше, чем больше достигаемая в реакторе степень превращения исходного реагента. Следовательно, при равном объемном расходе для достижения одинаковых результатов реактор идеального вытеснения должен иметь меньший объем, чем проточный реактор идеального смешения. Интенсивность реактора идеального вытеснения (1 = П / У =vcA,0xA/V)будет выше. Объяснить это можно более высокой скоростью реакции в реакторе вытеснения вследствие более высокой концентрации реагентов, одинаковых результатов. Реактор идеального вытеснения должен иметь меньший объем, чем проточный реактор идеального смешения. Интенсивность реактора идеального вытеснения (1 = П / У = ucA,0xA/V)будет выше. Объяснить это можно более высокой скоростью реакции в реакторе вытеснения вследствие более высокой концентрации реагентов.
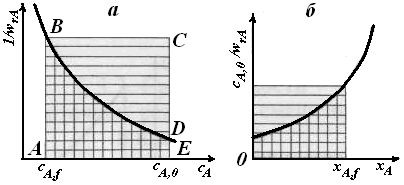
Рис. 5.7. Графическое сравнение проточных реакторов идеального смешения и идеального вытеснения как площадей геометрических фигур.
Однако не всегда стремятся к поддержанию более высоких концентраций исходных реагентов. Так, в § 3.3 было показано, что при проведении параллельных реакций разного порядка, в том случае, если порядок целевой реакции меньше порядка побочной реакции (n1 < п2),при низких концентрациях исходных реагентов обеспечиваются более высокие значения дифференциальной селективности (см., например, рис. 3.1).
Сравним проточные реакторы идеального вытеснения и идеального смешения при проведении параллельных реакций разного порядка
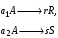 (I) (I)
по выходу целевого продукта R. Будем считать, что в обоих типах реакторов достигается одинаковая степень превращения исходного реагента А (т. е. заранее примем, что  B < B <  c). c).
Выход целевого продукта R для параллельных реакций (I)
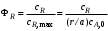 (5.14) (5.14)
[см. уравнение (1.11)].
Достигаемая на выходе из реактора концентрация целевого продукта cR будет определяться, с одной стороны, выбранным типом реактора, а с другой – кинетическими особенностями реакции (I), которые могут быть учтены через дифференциальную селективность φ', равную отношению скорости расходования реагента А на целевую реакцию к общей скорости его расходования. Для удобства дальнейшего рассмотрения представим систему стехиометрических уравнений (I) в эквивалентном виде:
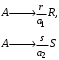 (Ia) (Ia)
(это нужно сделать, если стехиометрические коэффициенты а1 и а2 не равны). Скорость расходования А на целевую реакцию можно выразить через скорость образования целевого продукта, которая в соответствии с определением скорости [см. уравнение (3.3)] равна
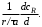
Тогда 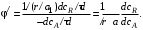 (5.15) (5.15)
Проинтегрировав дифференциальное уравнение (5.15), получим зависимость концентрации cR от дифференциальной селективности φ':
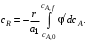
Подставляя выражение для cR в уравнение (5.14), получим
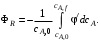 (5.16) (5.16)
Дифференциальная селективность φ', стоящая под знаком интеграла, является в общем случае убывающей или возрастающей функцией концентрации исходного реагента А, и в том случае, если концентрация сА не постоянна, для определения ФR нужно провести интегрирование этой функции. В частности, такую операцию необходимо сделать при расчете выхода продукта R в реакторе идеального вытеснения. Если сА постоянна по объему реактора и во времени (в стационарном реакторе идеального смешения), то и дифференциальная селективность φ' будет характеризоваться постоянным числовым значением, следовательно, уравнение (5.16) для реактора идеального смешения можно упростить:
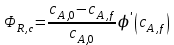 . (5.17) . (5.17)
Выход целевого продукта ФR, определенный по уравнениям (5.16) для реактора идеального вытеснения и (5.17) для реактора идеального смешения, можно представить графически в виде площадей криволинейной трапеции (ФR,B) и прямоугольника (ФR,С). Соотношение между этими площадями зависит от характера функции φ'(cА).
Если порядок целевой реакции превышает порядок побочной параллельной реакции (n1 > n2), выход целевого продукта ФR выше в реакторе идеального вытеснения (рис. 5.8, а). При этом, как указано выше, и среднее время пребывания для достижения заданной степени превращения реагентов меньше, чем в реакторе идеального смешения.
Если порядок целевой реакции меньше порядка побочной реакции (n1 < п2),более высокое значение выхода целевого продукта достигается в реакторе идеального смешения (рис. 5.8, б). Однако в рассматриваемом случае, т. е. при одинаковой степени превращения исходного реагента, среднее время пребывания 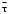 cрв реакторе идеального смешения больше, чем в реакторе идеального вытеснения. cрв реакторе идеального смешения больше, чем в реакторе идеального вытеснения.
Если целевая и побочная реакции имеют одинаковый порядок (n1= n2), выход целевого продукта при равной степени превращения исходного реагента не зависит от типа выбранного реактора (рис. 5.8, в).
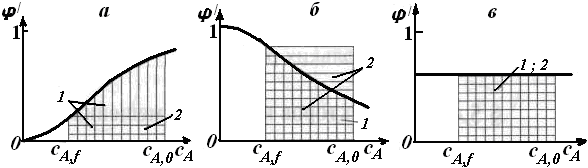
Рис. 5.8. Графическое сравнение выхода целевого продукта
в проточных реакторах идеального вытеснения (1) и идеального смешения (2) при проведении параллельных реакций разного порядка
Проведенное сравнение показывает, что в ряде случаев для достижения высокого выхода целевого продукта эффективнее реактор идеального вытеснения, а иногда реактор идеального смешения. При этом следует отметить, что даже при достижении более высокого выхода целевого продукта при равной степени превращения реактор идеального смешения имеет больший объем, чем реактор идеального вытеснения.
При сравнении не учитывался ряд факторов, ограничивающих применение аппаратов, работающих в режиме, близком к идеальному вытеснению. К ним следует отнести, например, большое гидравлическое сопротивление трубчатых реакторов, трудность чистки таких аппаратов и т. д. Конструктивно проточные аппараты с интенсивным перемешиванием проще, но обладают тем характерным недостатком, что в них устанавливается низкая концентрация исходного реагента (равная конечной) и, следовательно, низкой будет скорость химической реакции. Для использования преимуществ реакторов смешения и в то же время поддержания в реакционной системе более высоких концентраций реагентов можно создать каскад реакторов идеального смешения последовательным включением нескольких реакторов.
|
 Скачать 1.75 Mb.
Скачать 1.75 Mb.