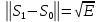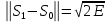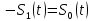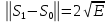ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ. Общая теория связи Что понимают под потенциальной помехоустойчивостью приёма дискретных сообщений
 Скачать 59.12 Kb. Скачать 59.12 Kb.
|
|
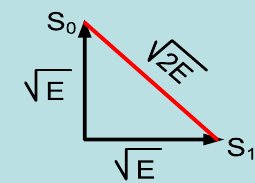
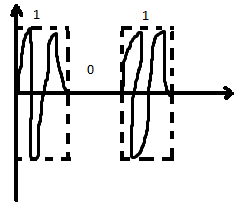
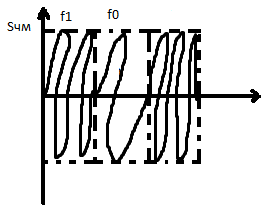
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11 по дисциплине: «Общая теория связи» 1.Что понимают под потенциальной помехоустойчивостью приёма дискретных сообщений? Под потенциальной помехоустойчивостью приема дискретных сигналов (сообщений) понимают минимальную возможную вероятность ошибки при приеме заданных сигналов на оптимальный приемник Котельникова. При приеме на реальный приемник, как правило, помехоустойчивость ниже потенциальной и ни при каких условиях не может превышать последнюю. Минимально возможное значение среднеквадратической ошибки min ε2U(t) при заданных условиях передачи (заданных сигналах, помехах, модели канала связи) определяет потенциальную помехоустойчивость приема непрерывных сигналов. Физически min ε2u(t) означает мощность помехи, поэтому расчет потенциальной помехоустойчивости сводится к вычислению минимально возможной мощности помехи на демодуляторе. Абсолютное значение мощности помехи не может быть объективной характеристикой ее влияния на сигнал, так как надо учитывать еще и уровень сигнала. Поэтому оценку помехоустойчивости приема непрерывных сигналов можно произвести количеством информации, получаемой при приеме этих сигналов. Рассмотрим потенциальную помехоустойчивость дискретной системы передачи информации при следующих исходных данных: - по каналу передаются двоичные символы (m=2).В этом случае каждому передаваемому символу будет соответствовать свои сигнал => на приемном конце системы будет точно известны 2 ожидаемых сигнала 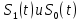 - в системе действует аддитивный белый шум. Такой шум характеризует нормальным распределением, функции плотности вероятностей и равновесный спектр плотности. - априорные вероятности передаваемых сигналов равны p(1)=p(0)=0,5 - принятый сигнал z(t) действующий на входе демодулятора носит случайный характер Алгоритм оптимального приема: 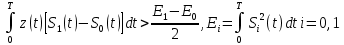 Если 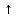 выполняется ,то система (демодулятор) принимает решение, что передавалась «1». Если неравенство не выполняется, то демодулятор принимает решение, что передавался «0». выполняется ,то система (демодулятор) принимает решение, что передавалась «1». Если неравенство не выполняется, то демодулятор принимает решение, что передавался «0».Если принять, что действительно передавался сигнал 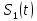 , то принимающий сигнал z(t) представляется собой аддитивную смесь этого сигнала и помехи: , то принимающий сигнал z(t) представляется собой аддитивную смесь этого сигнала и помехи: 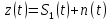 Вероятность ошибки p(0/1) (вероятность пропуска сигнала ) определяется вероятностью того, что алгоритм приема не выполняется. 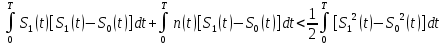 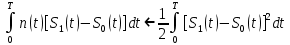 Аналогично получим, если будет передаваться «0» , т.е. будет иметь место вероятность ложной тревоги. В обоих случаях ,т.е. при передачи либо «0»,либо «1» вероятность ложной тревоги и вероятность пропуска сигнала оказывается равными : p(0/1)=p(1/0)=p (вероятность ошибки) В это случае сформулированный модемом двоичный канал оказывается симметричным 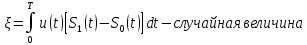 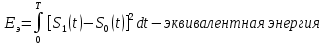 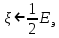 Случайная величина 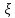 в силу того, что в канале действует белый шум также изменяется по случайному закону с тем же самым законом распределения как и помеха. Это означает, что её среднее значение (момент 1-го порядка) будет = 0. в силу того, что в канале действует белый шум также изменяется по случайному закону с тем же самым законом распределения как и помеха. Это означает, что её среднее значение (момент 1-го порядка) будет = 0.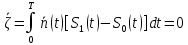 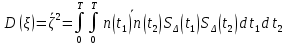 момент 2-го порядка момент 2-го порядкаУчитывая фильтрующие свойства 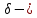 функции функции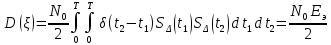 Дисперсия случайной величины 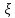 определяется 2 параметрами: определяется 2 параметрами:1)эквивалентной энергией передаваемых сигналов 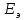 2)свойствами канала, которые отражены в спектре плотности шума 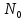 Вывод. Помехоустойчивость тем выше, чем больше эквивалентная энергия сигналов, независимо от формы используемых сигналов. 2. Эквивалентная энергия АМ, ЧМ и ФМ сигналов. Эквивалентная энергия 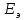 двух сигналов равна квадрату расстояния между сигнальными точками в гильбертовом пространстве. двух сигналов равна квадрату расстояния между сигнальными точками в гильбертовом пространстве.В двумерном пространстве точки сигналов для двоичной системы и трех видов модуляции имеют следующий вид:
В случае рассмотрения ЧМ ,АМ где учитываются средняя мощность сигналов и помехи у этих 2-х видов модуляции потенциальная помехоустойчивость оказывается равной. Однако, в реальных системах при АМ не удается достигнуть значение потенциальной помехоустойчивости из-за неустойчивости удержания порогового уравнения. Соотношение для эквивалентной энергии 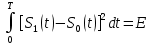 позволяет осуществлять оптимальный выбор сигналов 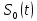 ) и ) и 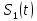 , обеспечивающих максимально возможную помехоустойчивость при заданной энергии сигналов Е. , обеспечивающих максимально возможную помехоустойчивость при заданной энергии сигналов Е. 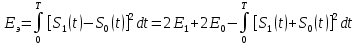 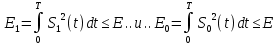 Д 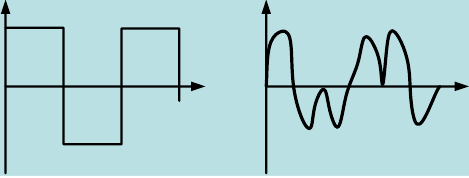 ля достижения максимальной эквивалентной энергии и соответственно максимально возможной помехоустойчивости , необходимо увеличить энергию сигналов ля достижения максимальной эквивалентной энергии и соответственно максимально возможной помехоустойчивости , необходимо увеличить энергию сигналов 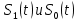 и уменьшить значение для интегрального выражения и уменьшить значение для интегрального выражения 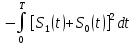 т.к квадрат суммы всегда положительная величина => её минимальное значение может быть равно только 0. Это возможно в том случае, если сигналы т.к квадрат суммы всегда положительная величина => её минимальное значение может быть равно только 0. Это возможно в том случае, если сигналы 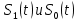 окажутся сдвинуты по фазе на 180 окажутся сдвинуты по фазе на 180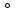 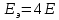 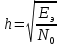 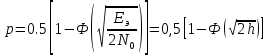
|