континуальный интеграл. Общие принципы ктп континуальный интеграл
 Скачать 25.44 Kb. Скачать 25.44 Kb.
|
|
общие принципы КТП Континуальный интеграл Интеграл Феймана Матричные элементы матрицы эволюции 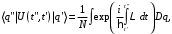 Где L-лангранжиан системы, N-нормировочная константа, 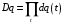 -мера в континуальном интеграле. -мера в континуальном интеграле.Матричный элемент матрицы эволюции определяется интегрированием функционального интеграла(с лангранжианом L) по всем траекториям в фазовом пространстве с заданными граничными условиями q’’ и q’ в моменты времени t’’ и t’ соответственно. Квантомеханическая амплитуда записывается в терминах классического функционала действия и меры Лиувилля. Примеры Гармонический осциллятор 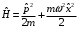 Действие имеет вид 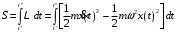 Континуальный интеграл гауссов. Перейдем к процедуре его вычисления. Гауссов интеграл считается по следующей процедуре: он равен (с точностью до некоторого множителя) подынтегральному выражению, вычисленному в точки экстремума показателя экспоненты, деленному на корень из определителя матрицы квадратичной формы в экспоненте. Показатель экспоненты это действие, как мы знаем из курса теоретической механике система проходит по траектории что бы действие было минимальным и удовлетворяет из этого уравнению Лагранжа. Поэтому решение уравнения движения классической системы на заданный Лагранжиан подставленный в выражение для действия и будет необходимым экстремумом. Вначале выясним уравнения классического движения. Из уравнения Лагранжа имеем такое уравнение движения 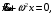 с г.у. с г.у. 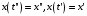 |
