лекции по геодезии. Общие сведения по геодезии. Предмет геодезии
 Скачать 15.89 Mb. Скачать 15.89 Mb.
|
|
Тема: Теодолитная съемка 1. Что такое теодолитная съемка. Виды съемок Теодолитной съемкой называется горизонтальная или контурная съемка местности, которая выполняется с помощью теодолита. Теодолитом измеряются горизонтальные углы и углы наклона. Линии измеряются стальной лентой и дальномерами различных конструкций. Для проектирования зданий, сооружений необходимо на район строительства иметь топографические материалы – планы, карты. При отсутствии таких материалов выполняют съемку данного участка местности. Существуют следующие виды съемок:
2. Сущность теодолитной съемки Теодолитная съемка выполняется с помощью теодолита и мерной ленты. В результате теодолитной съемки получают контурный план местности. С 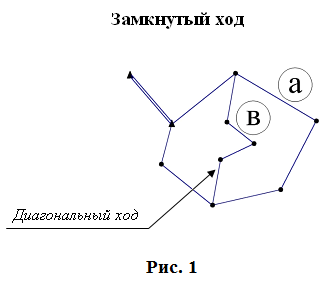 ъемку контуров выполняют на основе съемочных теодолитных ходов, которые прокладываются в виде: ъемку контуров выполняют на основе съемочных теодолитных ходов, которые прокладываются в виде:
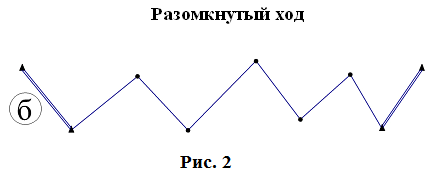 Теодолитная съемка складывается из следующих видов работ:
Длины сторон теодолитных ходов должны быть не более 350 м и не менее 20 м. 3. Прокладка теодолитных ходов. Привязка к пунктам геодезической сети Сначала намечаются поворотные точки теодолитного хода. Угловые измерения в теодолитных ходах выполняются способом приемов техническими теодолитами (Т30, 2Т30). Стороны измеряются стальной 20–метровой лентой в двух направлениях или дальномерами соответствующей точности. Для определения горизонтальных проложений измеряют углы наклона линии. Привязка теодолитных ходов заключается в измерении привычных углов между сторонами теодолитного хода и геодезической сети, обязательно с контролем.  4. Съемка ситуации Съемка ситуации заключается в привязке контуров и предметов местности к сторонам и вершинам теодолитного хода. Съемка ситуации может быть выполнена различными способами. 4.1. Способ прямоугольных координат (способ перпендикуляров) Ближайшая к контуру сторона хода принимается за ось абсцисс, точка А – за начало координат. Положение каждой точки определяется прямоугольными координатами X и Y. Перпендикуляры на местности строятся с помощью двузеркального эккера. Абсциссы отмеряют обычно с помощью мерной ленты, а ординаты – с помощью рулетки. Способ перпендикуляров применяется в основном при съемке вытянутых в длину контуров. 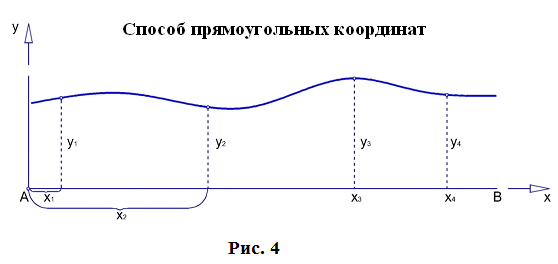 4.2. Способ полярных координат (полярный способ) 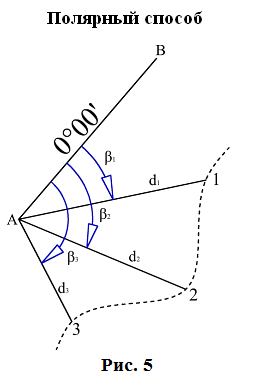 В этом случае ближайшая к контуру сторона теодолитного хода принимается за полярную ось, начало линии – за полюс. Положение точек 1, 2, 3 определяется полярными углами ß1, ß2, ß3; радиус – векторами d1, d2, d3. Полярные углы измеряются с помощью теодолита одним полуприемом, причем лимб ориентируется по сторонам хода, стороны измеряются с помощью нитяного дальномера. При съемке особо важных контуров – с помощью ленты. 4.3. Способ линейных засечек Треугольники стараются делать близкими к равносторонним. Линейная засечка применяется часто при съемке строений. В этом случае расстояния измеряются лентой или рулеткой. 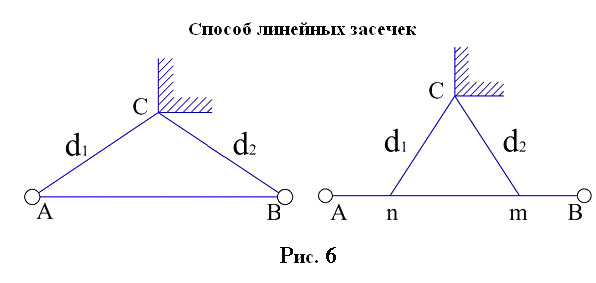 4.4. Способ угловых засечек Способ угловых засечек применяется в тех случаях, когда определить положение точки при помощи линейных измерений не удается. 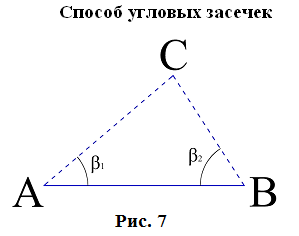 4.5. Способ створов Положение точки Р определяется расстоянием 2–Р вдоль линии 2–Е. Положение створной линии определяется расстоянием 4–Е. 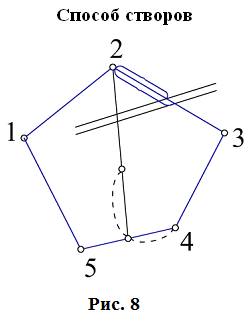 При съемке ситуации составляется абрис. Абрис – это схематический чертеж, составленный в произвольном масштабе. На абрисе зарисовывается снимаемая ситуация и записываются результаты выполняемых при съемке угловых и линейных измерений. Абрис составляется отдельно на каждую сторону теодолитного хода. На основе абриса производится нанесение контуров местности на план. ЛЕКЦИЯ 16 Тема: Обработка результатов полевых измерений. 1. Проверка полевых вычислений и определение поправок в измерения длин линий Камеральные работы при теодолитной съемке заключаются в вычислении координат точек теодолитного хода и в построении плана. Далее вычисляются средние значения длин линии: В каждую длину линии вводятся поправки по формуле: Поправки вводятся при: После уравнивания углов производится вычисление дирекционных углов всех сторон теодолитного хода. Вычисленные дирекционные углы переводятся в румбы. 2. Связь между дирекционными углами и горизонтальными углами теодолитного хода 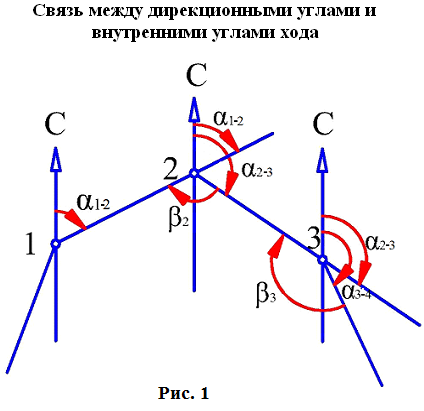 Дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс 1800 минус угол вправо по ходу лежащий. 3. Обработка угловых измерений замкнутого теодолитного хода 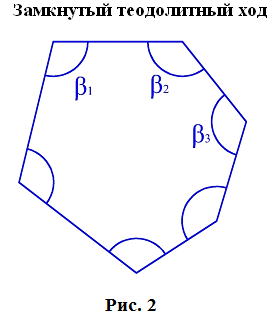 гдеfβ – угловая невязка. где n – вершина углов, следовательно: Если полученная невязка является допустимой, она распределяется поровну на все углы. Поправки в углы вводятся со знаком, противоположным знаку невязки. Сумма исправленных углов должна быть в точности равна теоретической сумме. 4. Угловая невязка разомкнутого теодолитного хода 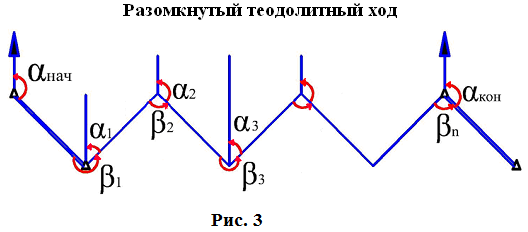 Для вычисления ∑βтеор. найдем дирекционные углы всех сторон хода: 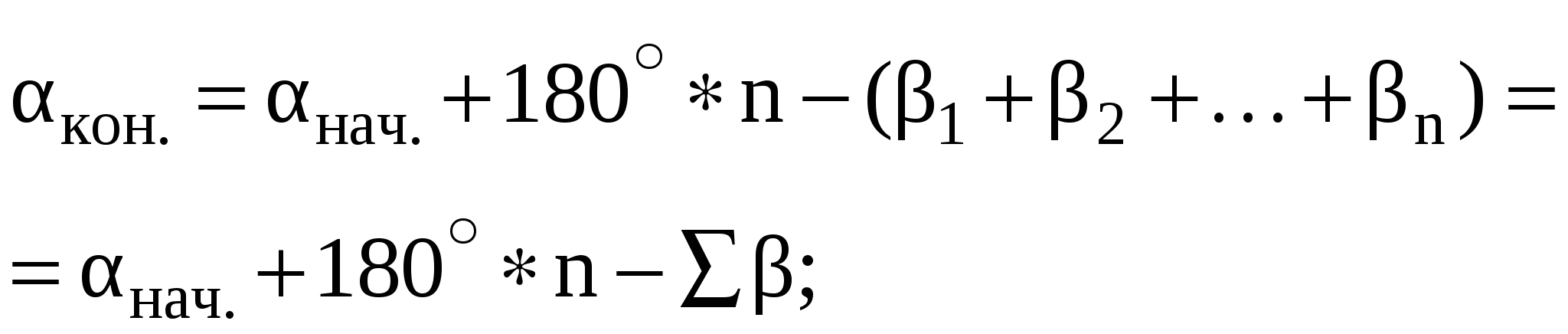 где αнач. и αкон. – дирекционные углы сторон опорной сети, тогда: Подсчет допустимой невязки и ее распределение производится так же, как и для замкнутого хода. 5. Невязки в диагональном ходе Диагональный ход является разомкнутым ходом, поэтому его обработка производится так же, как и у разомкнутого хода. Например, для следующего рисунка. 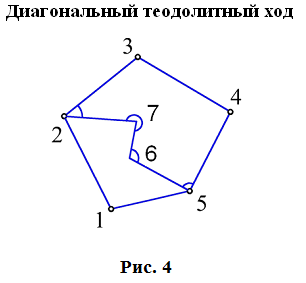 После обработки угловых измерений вычисляются дирекционные углы и румбы всех сторон хода. Причем вычисление дирекционных углов производится обязательно с контролем. 6. Прямая и обратная геодезические задачи 6.1. Прямая геодезическая задача: по координатам отрезка прямой (начала), его длине и направлению определить координаты конца отрезка  Прямая геодезическая задача применяется при вычислении координатных точек теодолитного хода. 6.2. Обратная геодезическая задача: по координатам начала и конца отрезка прямой найти его длину и направление 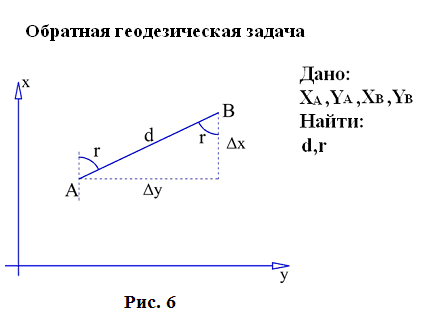 Далее вычисляют arctg и находят числовое значение румба. Название румба определяют по знакам приращений координат, от румба переходят к дирекционному углу. Длина линии может быть найдена по следующим формулам: Обратная геодезическая задача применяется при подготовке данных для перенесения проектов сооружений в натуру. 7. Уравнивание приращений координат 7.1. Вычисление координат точек теодолитного хода  Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам: Далее вычисляются невязки в приращениях координат замкнутого хода. 7.2. Вычисление невязок в приращениях координат замкнутого хода Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно: Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину fр – абсолютная невязка в периметре полигона. 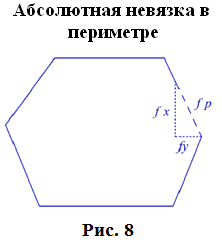 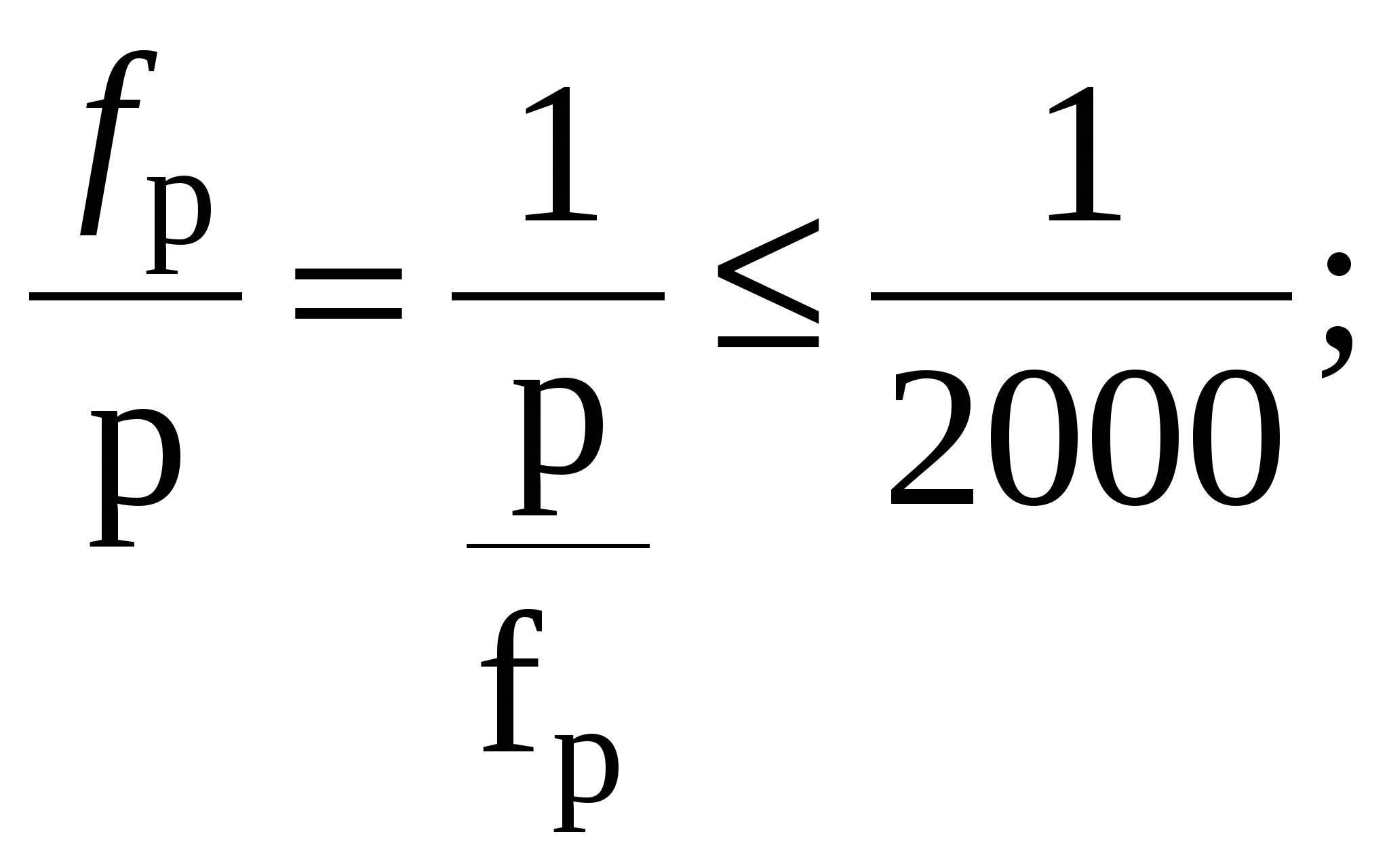 Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий. Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю. 7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода. 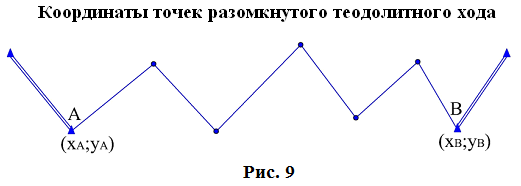 Для диагонального хода, например:  По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам: ЛЕКЦИЯ 17 Тема: Построение плана теодолитной съемки. 1. Построение плана Построение плана выполняются в следующей последовательности: 1) построение координатной сетки, 2) нанесение вершин теодолитного хода по координатам, 3) нанесение на план контуров местности, 4) оформление плана. 1.1. Построение координатной сетки Координатная сетка строится обычно со стороной 10х10 см. Используется 2 способа: 1) построение сетки с помощью линейки Дробышева: 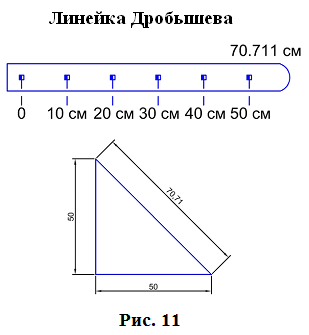 Построение сетки основано на построении прямоугольного треугольника с катетами 50x50 см и гипотенузой 70,711 см; 2) Построение сетки с помощью циркуля, измерителя и масштабной линейки: 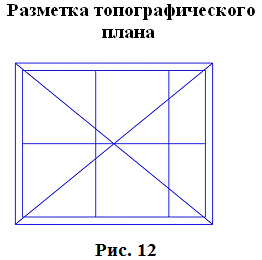 Этот способ применяется при размере плана меньше, чем 50 см. Сетка контролируется путем сравнения длин сторон или диагоналей квадратов. Допустимое отклонение – 0,2 мм. Построенную сетку подписывают координатами так, чтобы участок поместился. Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба. Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана. Например: 1:2000 – 0,6 м. Контуры местности наносятся на план в соответствии с абрисами. Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба. 2. Определение площадей участков Знать площади участков требуется для решения многих инженерно-технических и планово-экономических задач. Их можно определить по плану или по результатам измерений на местности. Вычисление площадей по результатам измерений на местности дает наиболее высокую точность и называется аналитическим способом. Различают вычисление площадей по координатам вершин замкнутого полигона и по результатам измерений элементов простейших фигур, на которые разбивается участок, и последующего вычисления и суммирования их площадей. По плану площадь вычисляется с меньшей точностью, так как кроме ошибок измерений на местности, здесь сказываются ошибки построений при создании плана, ошибки измерений по плану, деформация бумаги. Однако трудоемкость вычисления площади по плану значительно меньше. Существует несколько таких способов, среди которых можно выделить: графический способ и механический способ — с помощью специальных приборов. Способы определения площадей применяют комбинированно. Основную площадь землепользования, ограниченную теодолитными ходами, определяют по координатам (аналитическим способом) и принимают за теоретическую. Затем площадь отдельных угодий (полей и т. д.) определяют по плану, в основном применяя механический способ, и увязывают с площадью, полученной по координатам. 2.1 Понятие об аналитическом способе вычисления площадей Как уже говорилось, площади участков, ограниченных теодолитными ходами, можно вычислить наиболее точно по координатам их точек. Удвоенная площадь участка равна сумме произведений абсциссы каждой точки на разность ординат предыдущей и последующей точек или ординаты каждой точки на разность абсцисс последующей и предыдущей точек. Для контроля вычисления производят по обеим формулам. Перепишем их для полигона из n точек. 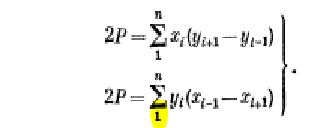 2.2 Понятие о геометрическом способе вычисления площадей Площади простых по форме участков вычисляют, разбив их предварительно на элементарные фигуры: треугольники, четырехугольники. При этом высоты, стороны и углы, необходимые для вычисления площадей, должны быть измерены на местности. 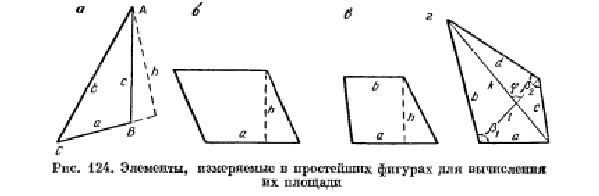 Способ основан на разбивке данной на плане территории на простейшие геометрические фигуры: треугольники, прямоугольники, трапеции. Стороны разбиваемых фигур должны быть прямыми линиями, удобными для измерения. Измерив в масштабе плана величины, необходимые для определения площади их площади основание, высоту, параллельные стороны, — определяют площадь каждой геометрической фигуры и затем берут их сумму. Запишем формулы для определения площади различных фигур. 1. Для треугольника где а, b, с — длины сторон; h — высота; С — угол между сторонами а и b треугольника, а р — полупериметр. 2. Для параллелограмма 3. Для трапеции 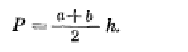 Эти формулы применяются и для вычислений площадей по данным измерений на местности (аналитический способ). Вычисление площади графическим способом тем точнее, чем крупнее масштаб плана. Чтобы проконтролировать результаты определения площади, надо повторить вычисление, меняя исходные данные. 2.3 Понятие об определении площадей палетками. Графическим способом определяют площади небольших участков с криво- линейными контурами с помощью палеток. Палетка изготовляется из листа прозрачного материала. Различают палетки прямолинейные и криволинейные. Прямолинейная палетка строится на листе бумаги, на который наносится сетка квадратов или параллельных линий. Для определения площади квадратной палеткой ее накладывают на участок, площадь которого нужно определить, и считают число целых квадратов, поместившихся внутри контура; доли неполных квадратов оценивают на глаз. Зная площадь одной клетки и число клеток, занимаемых контуром, перемножают их и получают площадь контура. Для определения площади участка палеткой с параллельными линиями ее накладывают так, чтобы крайние точки контура оказались между ее линиями. Таким образом, участок рассекается линиями палетки на фигуры, близкие к трапециям. Тогда, чтобы получить площадь контура, нужно сложить площади отдельных трапеций, которые определяют как произведение высоты трапеции на ее среднюю линию.  2.4 Понятие о механическом способе определения площади Измерение площадей механическим способом производится с помощью специального прибора — планиметра. Наиболее распространенным является полярный планиметр с рычагом переменной длины. Он состоит из двух рычагов — полюсного 3 и обводного 7. Имеет три точки опоры — колесо дополнительного счетного механизма 2, обводное стекло 6 и колесо 10. На одном конце полюсного рычага закреплен груз в нижней части которого имеется игла, перед началом измерений вдавливаемая в бумагу и служащая полюсом, вокруг которого вращается планиметр. 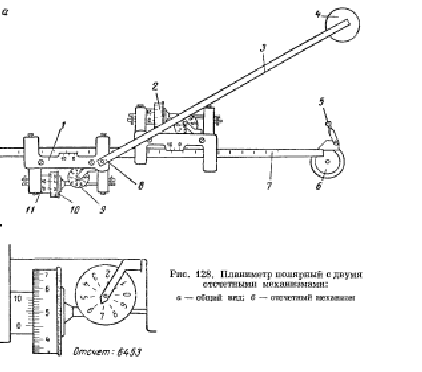 На конце обводного рычага закреплено стекло 6, на нижней поверхности которого выгравирована обводная точка. Удерживая планиметр за ручку 5, точкой обводят контур участка, площадь которого хотят измерить. На обводном рычаге- помещается каретка 1 счетного механизма, состоящего из счетного колеса 10 и счетчика целых оборотов 9. Для отсчетов по счетному колесу имеется верньер 11. При обводе контура участка ободок счетного колеса катится или скользит по бумаге. При измерении площади планиметром обводную точку совмещают с заранее выбранной точкой контура и делают четырехзначный отсчет. Первая цифра берется со счетчика целых оборотов, две последующие — число целых делений по счетному колесу относительно нулевого штриха верньера и последняя — число штрихов от нуля верньера до штриха, совпавшего с делением счетного колеса. Затем обводят контур по ходу часовой стрелки до возвращения в исходную точку и снова берут отсчет. Разность отсчетов выражает площадь участка в делениях планиметра. Чтобы получить площадь в гектарах или квадратных метрах, нужно знать цену деления планиметра. Качество результатов измерений планиметром зависит от формы участка, его величины, положения планиметра относительно участка и качества бумаги. Не рекомендуется измерять планиметром площади участков, меньших 10—15 см2 на карте или плане. Площади дорог, рек канав и других протяженных участков надежнее определять графическим или геометрическим способом. Приступая к измерениям, полюс планиметра следует расположить таким образом, чтобы угол между рычагами в процессе обвода не был слишком острым (не менее 30°). Для этого несколько раз бегло обводят контур, изменяя при необходимости положение полюса, чтобы положение рычагов было наиболее благоприятным, близким к 90°. Найдя такое положение, приступают к измерениям, при этом обводы делают равномерным движением руки. Контур обводят два раза, т. е. получают два значения площади участка. Расхождение между ними не должно быть больше 10 делений. Для определения цены деления планиметра берут участок, площадь которого S известна, например 2—3 квадрата координатной сетки, и измеряют ее при положении полюса вне измеряемого участка. Площадь получается в делениях планиметра, а, т.к., площадь уже известна в квадратных метрах, легко вычислить цену одного деления планиметра. Перед началом работ должно быть проверено, удовлетворяет ли планиметр следующим условиям: 1. Счетное колесо должно вращаться свободно. Регулировка производится перемещением центров, удерживающих колесо. При этом зазор между краем счетного колеса и верньером не должен быть более толщины папиросной бумаги. 2. Плоскость ободка счетного колеса должна бить перпендикулярна оси обводного рычага. Проверку производят путем обвода контура участка при двух положениях планиметра: при положении полюс вправо (ПП) и полюс влево (ПЛ) от обводного рычага. При этом нужно следить, чтобы угол между рычагами был не менее 30° и не более 150°. Условие считается выполненным, если разность полученных значений площадей составляет не более чем 1 : 250. Если условие не выполняется, то планиметром следует измерять площадь при двух положениях полюса и из полученных результатов брать среднее арифметическое. ЛЕКЦИЯ 18 |
