Прак. Занятие 3 Вычисление углов, площадей и объемов. Вычисление углов
 Скачать 129.27 Kb. Скачать 129.27 Kb.
|
|
Практическое занятие №3 Вычисление углов, площадей и объемов. Вычисление углов. Вычисление углов основано на формуле угла 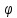 между векторами между векторами 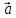 и и 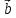 : : 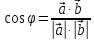 . .  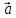  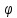 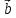 Скалярное произведение векторов 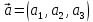 и и 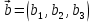 равно равно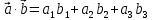 . .Модуль (длина) вектора 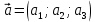 равна равна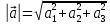 . .Задача 1. Найти угол между векторами  и и 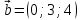 . . Решение. Пусть Решение. Пусть 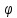 – угол между векторами – угол между векторами 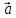 и и 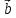 : : 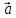  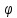 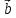 Тогда 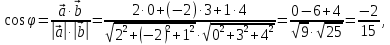 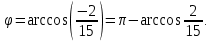 Задача 2. В треугольнике с вершинами 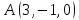 , , 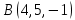 , , 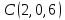 найти угол найти угол 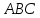 . .Решение.  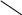 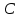  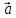 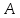  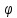 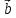 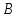 Неизвестный угол 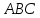 есть угол есть угол 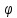 между векторами между векторами 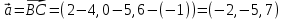 и 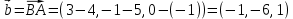 . .Тогда 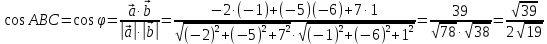 , ,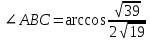 . .Вычисление площадей.   Вычисление площадей основано на формуле площади параллелограмма, построенного на векторах Вычисление площадей основано на формуле площади параллелограмма, построенного на векторах 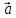 и и 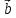 : :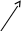 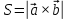 – модуль векторного произведения. – модуль векторного произведения.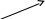 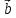 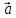 Векторное произведение векторов 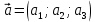 и и 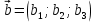 равно равно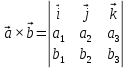 . .Площадь треугольника, построенного на векторах 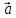 и и 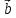 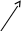 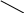 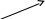 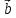 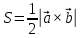 . .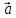 Пример. Найти векторное произведение векторов 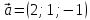 и и 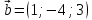 . .Решение. 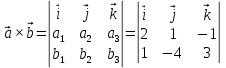 . .Определитель можно найти по правилу треугольников: 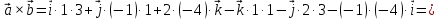 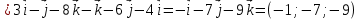 . .Однако часто такой определитель находят путём разложения по первой строке: 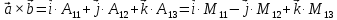 , ,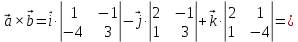 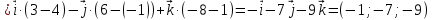 . .Задача 1. Найти площадь параллелограмма, построенного на векторах 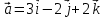 и и 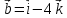 . .Решение. Найдём координаты векторов: 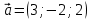 , , 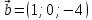 . Площадь параллелограмма, построенного на векторах . Площадь параллелограмма, построенного на векторах 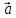 и и 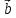 , можно найти по формуле , можно найти по формуле  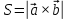 . . 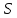 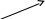 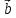 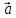 Сначала найдём векторное произведение 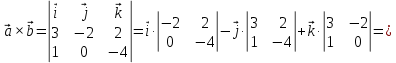 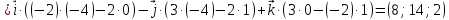 . .Тогда 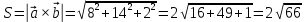 . .Задача 2. Найти площадь треугольника с вершинами 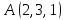 , , 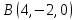 , , 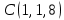 . .Решение.   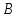 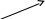 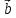 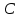 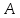 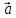 Треугольник 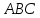 построен на векторах построен на векторах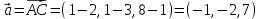 и 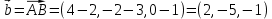 . .Тогда площадь этого треугольника можно найти по готовой формуле 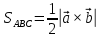 . .Найдем векторное произведение и его модуль 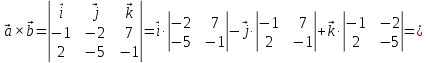 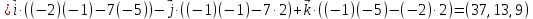 , ,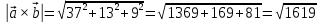 . .Тогда 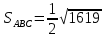 . .Вычисление объемов. Вычисление объемов основано на формуле объема параллелепипеда, построенного на векторах 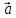 , , 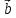 , , 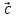 : : 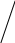 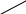 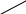     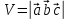 – модуль смешанного произведения. – модуль смешанного произведения.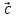 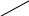  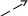 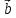  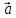 Смешанное произведение векторов 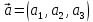 , , 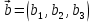 , , 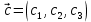 равно равно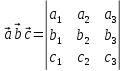 . .   Объем треугольной пирамиды, построенной на векторах Объем треугольной пирамиды, построенной на векторах 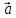 , , 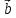 , , 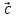 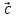 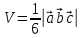 . .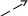 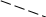 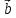  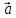 Задача 1. Найти объем параллелепипеда, построенного на векторах 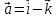 , , 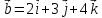 , , 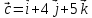 . .Решение. Найдём координаты векторов: 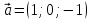 , , 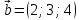 , , 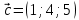 . Объем параллелепипеда, построенного на векторах . Объем параллелепипеда, построенного на векторах 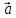 , , 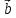 , , 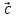 можно найти по формуле можно найти по формуле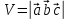 . .        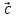 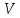    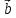  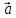 Найдем смешанное произведение 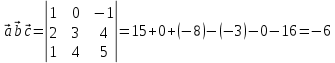 . .Тогда 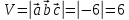 . .Задача 2. Найти объем треугольной пирамиды с вершинами  , , 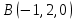 , , 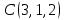 , , 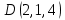 . .Решение.   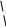 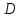 . 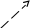  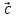 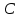 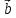  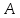 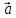 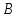 Данная пирамида построена на векторах 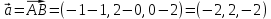 , ,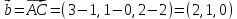 , ,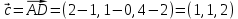 . .Тогда объем этой пирамиды можно найти по готовой формуле 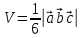 . .Найдем смешанное произведение 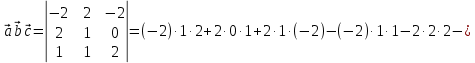 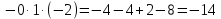 . .Тогда 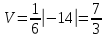 . . |
