лекции по геодезии. Общие сведения по геодезии. Предмет геодезии
 Скачать 15.89 Mb. Скачать 15.89 Mb.
|
Тема: Элементы теории ошибок измерений.
Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений. При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые, систематические и случайные. К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения. Систематические ошибки происходят от неизвестного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях. Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений. В основу теории ошибок положены следующие свойства случайных ошибок: 1. Малые ошибки встречаются чаще, а большие реже. 2. Ошибки не превышают известного предела. 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются. 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений. По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения. Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами. Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей. , 2. Арифметическая средина. Если одна величина измерена n раз и получены результаты: l1, l2, l3, l4, l5, l6,….., ln, то  Величина x называется арифметической срединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений: l 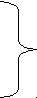 1 – x = v1 1 – x = v1 l2 – x = v2 l3 – x = v3 . . . . . . . . ln – x = vn Или в общем виде получим: [ l ] – nx = [v] Тогда [v] = 0. 2. Средняя квадратическая ошибка. Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле: 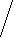  [v2] m  = √ n - 1 = √ n - 1где [v2] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле: 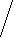  m [v2] M = ----------- = √ --------------  √n n ( n – 1 ) √n n ( n – 1 )Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3m. Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной ве- личины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м, при m = 2 см равна m/l = 1/5500. Пример. Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:
По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна 2,3 1 ---------- = ----------- 22520 9 800
Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:
измеренной величины по формуле арифметической средины х = [1]/n.
которая может служить допустимым значением погрешностей аналогичных измерений. ЛЕКЦИЯ 7 Тема: Геодезические сети. Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками). Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат. Геодезические сети подразделяют на плановые и высотные: первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот. Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин. Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным. Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.
Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети. 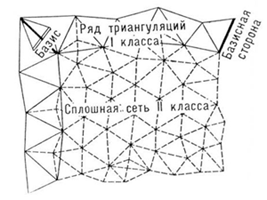 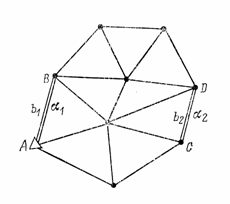 Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон. 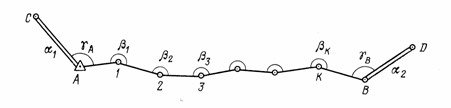 При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны. 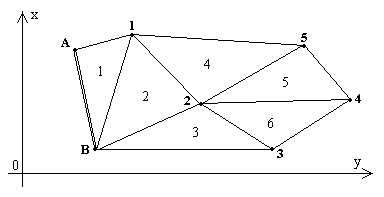 Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды. Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов. Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства. Государственные высотные геодезические сети создают для распространения по всей территории страны единой системы высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металличе- ской пластине, укрепленной в устое моста через обводной канал в Кронштадте. Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколь- ко пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны. На незастроенной территории расстояния между реперами составляют 5...7 км, в го- родах сеть реперов в 10 раз плотнее. Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса. Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.
Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению — постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д. Постоянные знаки. Их закрепляют подземными знаками — центрами. Конструкции центров обеспечивают их сохранность и неизменность положения в течение длительного периода времени. Как правило, подземный центр представляет собой бетонный монолит , закладываемый ниже глубины промерзания грунта и не в насыпной массив. У поверхности земли в монолите устанавливают чугунную марку, на которой наносят центр в виде креста или точки. Положению этого центра соответствуют коор- динаты Хи Y и во многих случаях отметки.  Для того чтобы с одного знака был виден другой (смежный), над подземными центрами устанавливают наружные знаки в виде металлических или деревянных трех- или четырехгранных пира- мид или сигналов.  Пирамиды или сигналы имеют высоту 3...30 м и более. Геодезический сигнал с под- земным центром и столиком предназначен для установки измерительных приборов и на- стила при работе на нем наблюдателя. Верх сигнала или пирамиды заканчивается визир- ной целью , на которую при измерении углов направляют зрительную трубу теодолита. На столик устанавливают также отражатель, если измеряют расстояния между пунктами светодалъномером. Для спутниковых измерений сигналы и пирамиды строить не надо. Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными. Координаты всех пунктов плановой геодезической сети, а также отметки пунктов высотной геодезической сети заносятся в специальные каталоги, в которых кроме названия пунктов дается описание их местоположения. Иногда для различных целей могут создаваться местные геодезические сети. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей). Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ. ЛЕКЦИЯ 8 Тема: Угловые измерения на местности. Основными элементами любых геодезических работ на местности являются угловые и линейные измерения. Для производства угловых измерений служат специальные приборы, называемые теодолитами. 1. Теодолит. Устройство теодолита Теодолит – это геодезический прибор, предназначенный для измерения горизонтальных углов, углов наклона и расстояний.  В соответствии с действующим ГОСТом в настоящее время промышленностью выпускаются теодолиты следующих типов:  Основными частями любого теодолита являются лимб, алидада, зрительная труба. 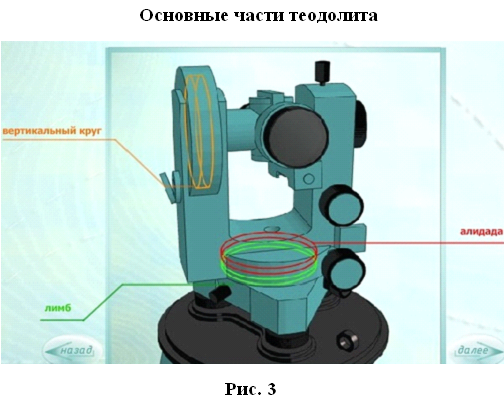 Угломерный круг, по краю которого нанесена шкала с градусными делениями, называется лимбом. В плоскости угломерного круга с лимбом вращается второй круг – алидада. 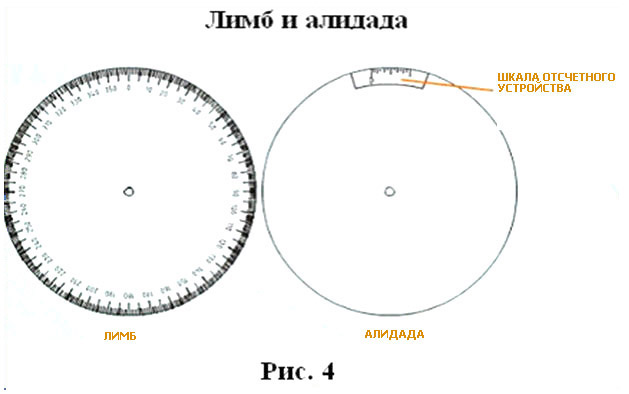 На алидаде имеется устройство для отсчета по лимбу. В современных теодолитах угломерные круги стеклянные, такие теодолиты называются оптическими. Алидада жестко связана со зрительной трубой с помощью колонок. Лимб, алидада и зрительная труба имеют закрепительные и наводящие винты.  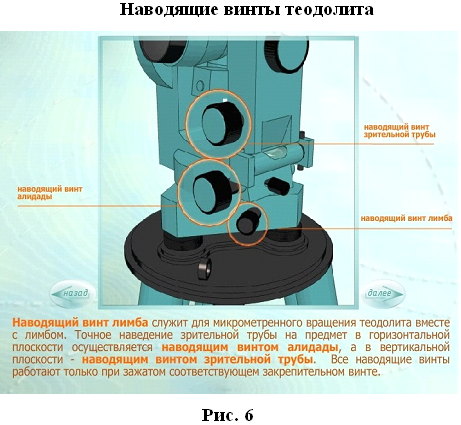 Плоскость лимба приводится в горизонтальное положение с помощью трех подъемных винтов и цилиндрического уровня. Центр лимба устанавливается над вершиной измеряемого угла. Для грубой наводки трубы на предмет служит оптический визир. Для измерения вертикальных углов наклона имеется вертикальный круг. Для производства отсчетов по лимбу рядом с окуляром зрительной трубы располагается микроскоп, свет в который направляется с помощью специального зеркальца. Для прикрепления теодолита к штативу служит становой винт. 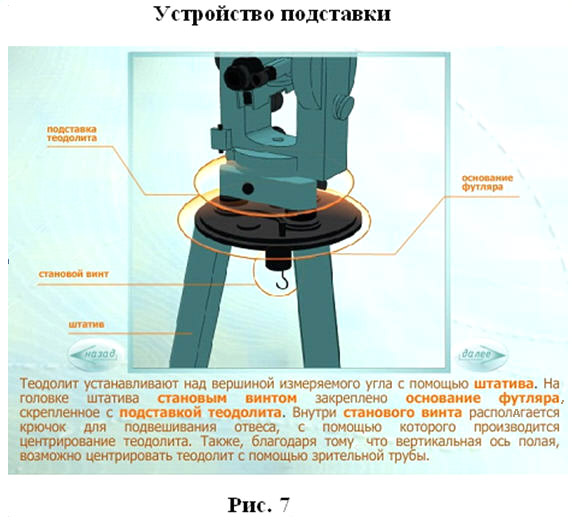 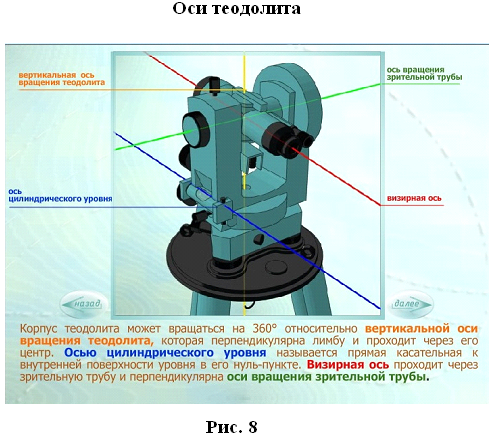 2. Отсчетные устройства При измерении углов производится отсчет по лимбу. Угловая величина дуги, соответствующая одному делению шкалы лимба, называется ценой деления лимба. 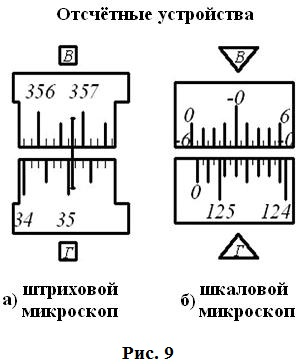 Отсчет по лимбу производится относительно индекса, нанесенного на алидаду. Для оценки долей деления лимба служат отсчетные устройства. В оптических теодолитах в качестве отсчетных устройств служат штриховые (Т30) и шкаловые (2Т30 и Т15) микроскопы.  3. Уровни Уровни бывают круглыми и цилиндрическими. Цилиндрический уровень состоит из стеклянной трубки, верхняя часть которой представляет дугу большого радиуса. На верхней части ампулы имеется шкала делений через 2 мм. Центральный штрих шкалы называется нуль – пунктом. Прямая, касательная к внутренней поверхности уровня в его нуль–пункте, называется осью цилиндрического уровня. Чем больше радиус, тем меньше цена деления и тем уровень точнее. 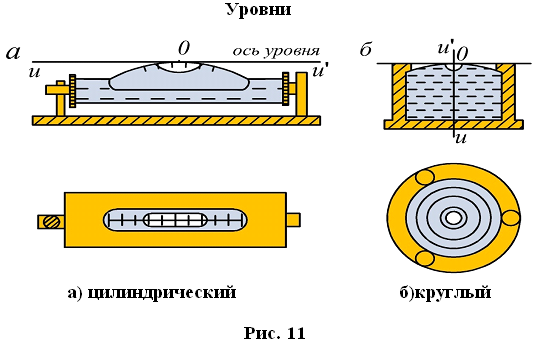 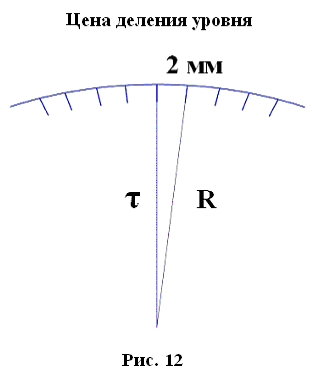 4. Зрительные трубы Зрительная труба геодезических приборов состоит из объектива и окуляра. Трубы большинства геодезических приборов дают обратное (перевернутое) изображение предмета. Вблизи переднего фокуса окуляра помещается металлическое кольцо, называемое диафрагмой со стеклянной пластинкой, на которой награвированы тонкие нити, составляющие сетку нитей. Сетка нитей снабжена четырьмя исправительными винтами, позволяющими перемещать сетку нитей в своей плоскости. 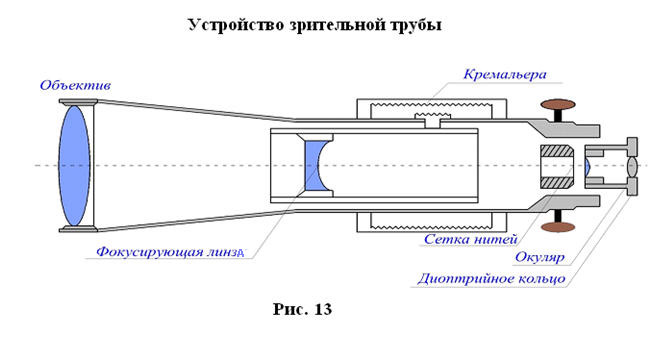 Прямая, соединяющая перекрестки сетки нитей с оптическим центром объектива, называется визирной осью трубы. Установка трубы для наблюдений складывается из установки ее «по глазу» и «по предмету». При недостаточно тщательной фокусировке трубы будет наблюдаться перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром. Перемещение предмета относительно сетки при изменении положения глаза наблюдателя перед окуляром называется параллаксом сетки нитей. Устраняется дополнительным вращением кремальеры. 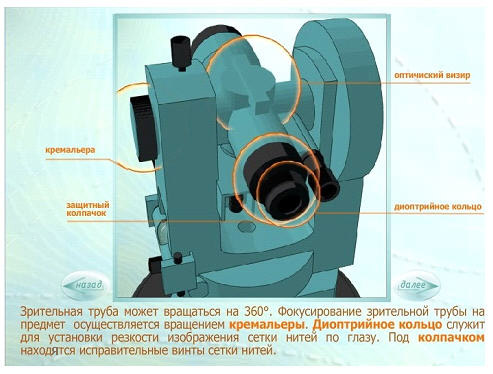 Установка трубы «по глазу» заключается в получении резкого изображения сетки нитей. Выполняется перемещением диоптрийного кольца.  Установка трубы «по предмету» выполняется с помощью кремальеры, при этом внутри трубы перемещается фокусирующая линза (труба с внутренней фокусировкой). ЛЕКЦИЯ 9 | ||||||||||||||||||||||||||||||||||
