Решение. Результат измерения в соответствии с указанным методом определяется на основании закона Ома по показаниям приборов
 Скачать 41.43 Kb. Скачать 41.43 Kb.
|
|
5.1 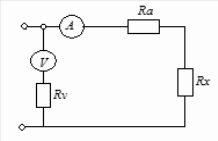 1) Методом амперметра-вольтметра 1) Методом амперметра-вольтметраизмеряется сопротивление RX (см. рису- нок). При этом RX определяется в соот- ветствии с законом Ома по показаниям амперметра IA и вольтметра UV . Извест- но, что IA= 0,03 А, UV = 9В, RA = 3 Ом, RV =10 кОм. Определить абсолютную погрешность измерения, величину поправки, исправленный результат измерения, относительную погрешность измерения RX . Классифицировать вид измерения, погрешность измерения, метод устранения погрешности. Решение. Результат измерения в соответствии с указанным методом определяется на основании закона Ома по показаниям приборов Rх изм = 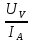 = =  = 300 Ом = 300 ОмАбсолютная методическая погрешность измерения ∆R = Rх изм – Rx ист = 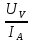 - Rx ист = - Rx ист = 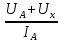 - Rx ист = - Rx ист =  + +  - Rx ист = - Rx ист =  + Rx ист - Rx ист = + Rx ист - Rx ист =  = RA = 3 Ом, = RA = 3 Ом,где Ux и UA – падения напряжения на Rx и RA соответственно, Ix – ток через Rx Относительная методическая погрешность измерения δ = 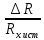 Найдем RΧ ист, это исправленный результат измерения с учетом внесенной поправки ΑR = −ΔR = −RΑ = - 3 Οм , тогда RΧ ист = RΧ изм + ΑR = (300 − 3) Οм = 297 Οм δ = 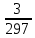 ·100% = 1,01 % ·100% = 1,01 %Погрешность измерения является в данном случае методической, т.к. обусловлена неидеальностью метода измерения (по условию задачи амперметр измеряет силу тока абсолютно точно, т.е. инструментальные погрешности отсутствуют); систематической (т.к. при многократных измерениях погрешность остается постоянной). Метод амперметра—вольтметра является косвенным, так как основан на использовании закона Ома, по которому измеряемое сопротивление прямо пропорционально падению напряжения на нем и обратно пропорционально силе тока, протекающего по нему. Отсюда следует общеизвестный вывод: для обеспечения малой методической погрешности измерения амперметр должен обладать малым сопротивлением, т.е. должно выполняться условие RА << Rх, а также использовать при подключении приборы высокого класса точности. Ответ: ∆R = 3 Ом, ΑR = -3 Ом, RΧ ист = 297 Ом, δ = 1,01 % 5.2 10) При измерении мощности сигнала были получены следующие результаты: Р′ = 25,2 мВт; составляющие систематической погрешности θ1 = 0,4 мВт, θ2 = 0,3 мВт; составляющие случайной погрешности в виде границ доверительных интервалов ε0,95 = 0,15 мВт, ε0,9 = 0,1 мВт. Случайные погрешности распределены по нормальному закону. Записать результат измерения при доверительной вероятности РД = 0,95. Решение. Для определения общей погрешности измерения необходимо просуммировать отдельно составляющие систематической погрешности θi , отдельно составляющие случайной погрешности Si и затем сложить полученные суммарные значения НСП и случайной погрешности в соответствии с правилами суммирования погрешностей. Границы доверительного интервала случайной погрешности ε = tн (ΡД ) ⋅ Si, где tН (PД ) — коэффициент нормального закона распределения. При PД = 0,95 tН = 1,96, 0,15 = 1,96 · S1; S1 = 0,08 мВт PД = 0,90 tН = 1,65, 0,10 = 1,65 · S2; S2 = 0,06 мВт Границы систематической погрешности равны: θ∑ (РД) = k (РД) 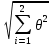 = k (0,95) = k (0,95)  = 1,1 = 1,1 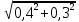 = 0,55 мВт = 0,55 мВтСКП систематической погрешности: Sθ = 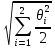 = = 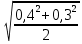 = 0,35 = 0,35 В условии задачи отсутствует указание величин коэффициента корреляции, следовательно, составляющие случайной погрешности некоррелированы (независимы) и суммарная СКП: S∑ = 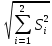 = =  = = 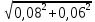 = 0,1 мВт = 0,1 мВтГраницы доверительного интервала случайной погрешности εΣ = tн (ΡД )⋅ SΣ =1,96 ⋅ 0,1 = 0,196 Далее необходимо сложить систематическую и случайные составляющие погрешности. Сначала определяем соотношение 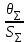 = =  = 5,5 = 5,5Тогда ∆Робщ (РД) = K∑ · Sобщ, где K∑ = 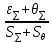 = = 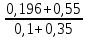 = 1,66 = 1,66Sобщ =  = = 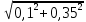 = 0,36 = 0,36∆Робщ (0,95) = 1,66 · 0,36 = 0,5976 мВт Результат измерения с учетом правил округления погрешности и результата запишется в следующем виде Р = Р´ ± ∆Робщ , РД, Р = (25,2 ± 0,6) мВт, РД = 0,95 Ответ: Р = (25,2 ± 0,6) мВт, РД = 0,95 5.3 1) Вольтметр имеет предел измерения Uшк1 =1В , класс точности γ1 = 1.0 , входное сопротивление Rv = 1 кОм. Рассчитать величину и допустимую относительную погрешность добавочного сопротивления, необходимого для изменения предела измерения до Uшк2 = 10В и достижения общего класса точности γ2 = 0.5. Решение. Для расширения шкалы в n раз измерений вольтметру последовательно подключают добавочное сопротивление, величина которого рассчитывается по формуле: R доб = R V · (n − 1), где RV — внутреннее сопротивление вольтметра; n – коэффициент расширения предела измерения: n = 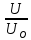 , ,U0 — максимальное напряжение, которое можно было измерять до подключения добавочного сопротивления; U — максимальное напряжение, которое необходимо измерять данным вольтметром (после подключения добавочного сопротивления). 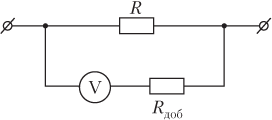 R доб = 1000 ·( 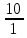 -1) = 9000 Ом = 9 кОм -1) = 9000 Ом = 9 кОмОсновная погрешность прибора с добавочным резистором: δR = 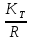 · 100 % = · 100 % =  · 100 % = ± 0,01 % · 100 % = ± 0,01 %Ответ: δR = ± 0,01 % 5.4 5) При многократных измерениях индуктивности получены следующие результаты: 45; 45.4; 45.8; 44.2; 44.6; 45; 44.6; 45.4; 48.2; 45 мкГн. Записать результат измерения при доверительной вероятности PД = 0.9. Решение. Найдем среднее арифметическое значение измеряемой величины по формуле: 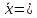 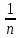 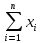 , ,где n – число измерений.  · (45+45,4+45,8+44,2+44,6+45+44,6+45,4+48,2+45) = · (45+45,4+45,8+44,2+44,6+45+44,6+45,4+48,2+45) = 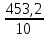 = 45,3 мкГн = 45,3 мкГн Вычисляем среднее квадратическое отклонение единичных результатов: S =  S = 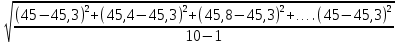 S = 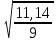 = 1,1 = 1,1Предполагая, что погрешность распределена по нормальному закону, исключаем «промахи», т.е. измерения с грубыми погрешностями, для которых  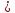 tгр (РД, n), tгр (РД, n),где xi- подозрительный на наличие промаха результат измерения из полученной выборки; tгр (РД, n) - коэффициент допускаемых нормированных отклонений, выбирается при заданных РД и n из таблицы П.2 Приложения. Определяем для нашей задачи, tгр(0,95; 10) = 2,414  = 1 < 2,414 = 1 < 2,414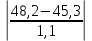 = 2,636 > 2,414 = 2,636 > 2,414Условие промаха выполняется, то есть L9 = 48,2 мкГн — промах. Его удаляем из ряда многократных измерений. Теперь n = 9 . Продолжаем проверку на наличие промахов. Пересчитываем вновь значения 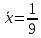 · (45+45,4+45,8+44,2+44,6+45+44,6+45,4+45) = · (45+45,4+45,8+44,2+44,6+45+44,6+45,4+45) =  = 45 мкГн = 45 мкГн S =  S = 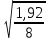 = 0,5 = 0,5По таблице определяем новые границы tгр (0,95;9) = 2,349. Проверяем условие промаха: 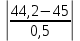 = 1,6 < 2,349 = 1,6 < 2,349 = 1,6 < 2,349 = 1,6 < 2,349Грубые промахи исключены. Вычисляем среднее квадратическое отклонение среднего арифметического (СКО результата измерений): 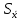 = = 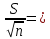 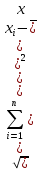 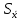 = =  = 0,2 = 0,2Определяем доверительные границы случайной погрешности при заданной доверительной вероятности Р = 0,90: ɛ =  · ·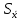 , ,где  – коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа измерений n. Выбираем коэффициент t из таблицы – коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа измерений n. Выбираем коэффициент t из таблицы (t = 1,9) ɛ = 1,9 · 0,2 = 0,4 Запишем окончательный вариант: (45,0 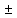 0,4) мкГн 0,4) мкГнОтвет: (45,0 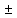 0,4) мкГн 0,4) мкГн5.5 2) Определить результат и абсолютную погрешность косвенного измерения реактивной мощности Q =U × I sinϕ по результатам прямых измерений: – показания вольтметра класса точности 2.5 с пределом измерения 100 В ,  U = 75 В ; U = 75 В ;– показания амперметра класса точности 1.0 с пределом измерения 10 А, I = 4 А , ϕ = 30° ±1° . Записать результат измерения. Решение. Известно, что результат косвенных измерений определяется представленной функциональной зависимостью при подстановке в нее результатов измерений аргументов. В нашем случае Q = U · I · sinϕ = 75 · 4 · sin30˚ = 150 Вт В общем виде погрешность косвенного измерения ∆y = 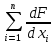 · ∆xi · ∆xiгде xi- аргументы функции F, Δxi - их абсолютные погрешности, y - измеряемая косвенным образом величина, 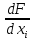 - частные производные функции по соответствующим аргументам. - частные производные функции по соответствующим аргументам. Определим абсолютные погрешности аргументов заданной зависимости: максимальная абсолютная погрешность амперметра:  = =  = =  = ± 0,04 А = ± 0,04 Агде  - относительная погрешность прибора, заданная классом точности, в данной задаче δ = ± 1,0 %; - относительная погрешность прибора, заданная классом точности, в данной задаче δ = ± 1,0 %; - нормирующее значение шкалы, равно пределу измерения. - нормирующее значение шкалы, равно пределу измерения.Аналогично для вольтметра:  = = 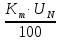 = =  = ± 2,5 В = ± 2,5 Вгде Кт - класс точности прибора Так как погрешности аргументов заданы границами интервалов, которые определены, в том числе, и с помощью измерительных приборов, то можно считать, что эти погрешности распределены равновероятно. Тогда, в соответствии с правилами суммирования погрешностей, общая погрешность при заданной доверительной вероятности PД может быть определена выражением: ∆Q(РД) = k (РД)  Величина доверительной вероятности в условии задачи не указана. Необходимо воспользоваться известными рекомендациями, в которых для технических электрорадиоизмерений применяется PД = 0,95. Тогда ∆Q(0,95) = 1,1 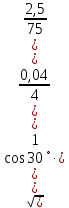 = 1,04 Вт = 1,04 ВтЗапишем результат измерения с учетом правил округления Q = (150 ± 1) Вт, РД = 0,95 Ответ: Q = (150 ± 1) Вт, РД = 0,95 |
