Практическое задание №2. ПЗ2 — копия. 2 Необходимо определить числовое значение конечного объекта

• Название: 2 Необходимо определить числовое значение конечного объекта
• Анкор: Практическое задание №2
• Дата: 21.06.2022
• Размер: 133.02 Kb.
• Имя файла: ПЗ2 — копия.docx
• Тип: Документы; #607025

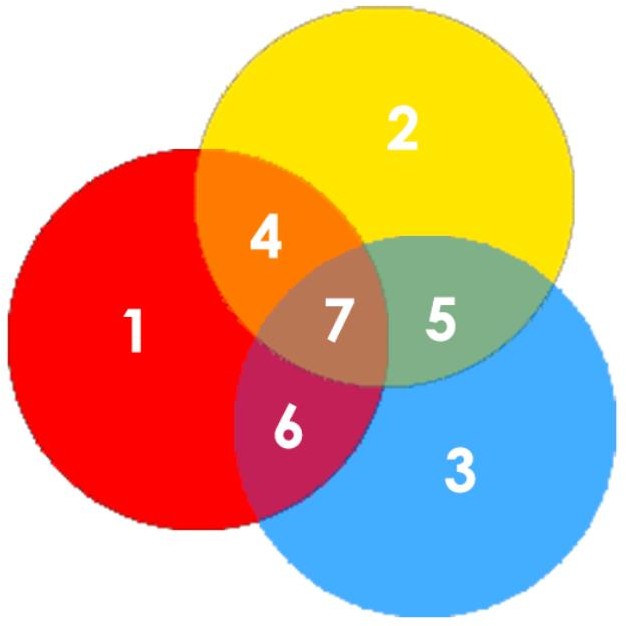
Задание №1

№2 Необходимо определить числовое значение конечного объекта.

№3 Необходимо определить числовое значение величины начального состояния объекта.

№4 Необходимо определить числовое значение конечного объекта.

№5 Необходимо определить числовое значение величины отношения между начальным и конечным состояниями

№6 Необходимо определить числовое значение величины отношения между начальным и конечным состояниями.

№7 Необходимо определить числовое значение величины отношения между начальным и конечным состояниями

№8 Необходимо определить числовое значение величины отношения между начальным и конечным состояниями

Задание №2

1. 
    
   60% - рисование;
   
2. 
   50% - гимнастика;
   
3. 
   50% - музыка;
   
4. 
   30% - рисование и гимнастика;
   
5. 
   20% - гимнастика и музыка;
   
6. 
   40% - рисование и музыка
   
7. 
   10% - все кружки
   

1. 
   Не желают водить детей в кружки – 40% родителей
   
2. 
   Выбрали не менее двух кружков (30-10)+(20-10)+(40-10)+10= 70 (%)
   

Задание №3

Построим вариационный ряд – выборку в порядке возрастания: 5, 5, 5, 10, 10, 15, 20, 20, 20, 20 Запишем таблицу частот:

	5	10	15	20
	3	2	1	4

Построим полигон частот: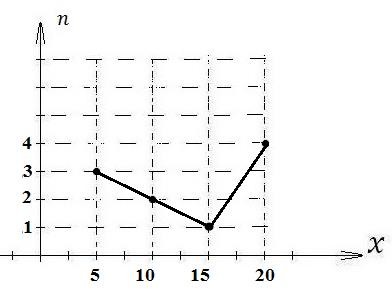


Общее число значений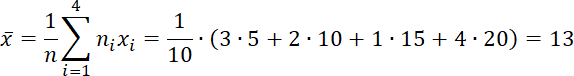



 Найдем выборочное среднее :

 Найдем выборочную дисперсию   :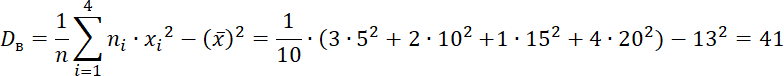


^{Поскольку наибольшая вероятность достигается при   равном 20, то мода}
 .
^{Медианой дискретной случайной величины   с 10 значениями называется среднее арифметическое 5 и} 6 элемента:



Частоты   определим по формуле:

	5	10	15	20
	3	2	1	4
	0,3	0,2	0,1	0,4

Функция распределения имеет вид: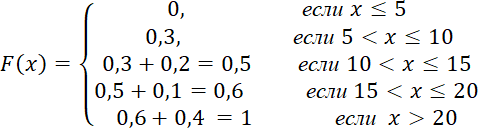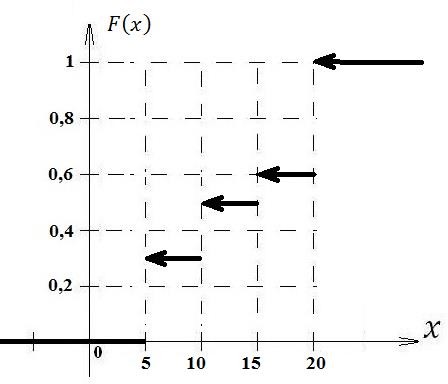
 

Задание №4

1. 
   4,45575250 до шести знаков = 4,455753
   
   4,45575250 до пяти знаков = 4,45575
   
   4,45575250 до четырёх знаков = 4,4558
   
   4,45575250 до трех знаков = 4,456
   
   4,45575250 до двух знаков = 4,46
   
   4,45575250 до одного знака = 4,5
   
   4,45575250 до целого числа = 4
   
   b) Округляя число 12,75 получаем 12,8. Прибавляем 1 к десятым, потому что сотые больше 5.
   Абсолютная погрешность равна модулю разницы между точным и округленным числом, 12,8 – 12,75 = 0,05
   Относительная погрешность равна абсолютной, деленной на приближенное значение, выраженное в процентах, 0,05 / 12,8 * 100% = 0,003%
   
   c) Определение: «Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не больше единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной».
   х = 13,75 ± 0,03
   0,03 - граница абсолютной погрешности
   Единица последнего разряда - 0,01 (сотые)
   0,03 > 0,01
   значит цифра 5 - сомнительная
   0,03 < 0, 1 - значит цифра 2 - верная
   Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.
   Значит 3; 1 - также верные цифры
   В записи приближенного  значения числа сохраняют только верные цифры, а сомнительные цифры округляют, значит
   х = 13,3
   

З 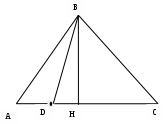адание №5

Дано: треугольник ABC, AD=3см, DC=10см, S треугольника ABC=39 см².
Найти: S треугольника ABD
Решение:
BH – общая высота, следовательно S_ABC/S_ABD = AC/AD
39/S_ABD = 13/3
13 S_ABD = 39*3
S_ABD = 39*3/13 = 9

Ответ: 9 см².

Задание №6

Д ано: параллелограмм ABCD, BF=4 см, FC=2 см, ∠ABC=150⁰.

Найти: S параллелограмма ABCD

Решение: Накрест лежащие углы BFA и FAD равны, AF — биссектриса ∠BAD, следовательно, ∠ BFA и ∠ FAD = ∠ BAF

Значит, треугольник BFA равнобедренный и  AB=BF=4
По формуле площади параллелограмма находим: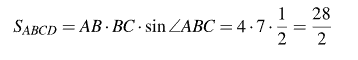


Ответ: 14

Задание №7

Дано: АBCDA1B1C1D1 – прямая призма

A 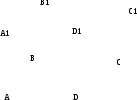BCD – ромб
АА1=12

BD =6

AC = 8
Найти: Sпов
Решение:
Сторона ромба a выражается через его диагонали  и  формулой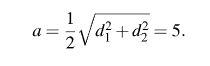

Найдем площадь ромба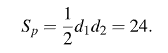

Тогда площадь поверхности призмы равна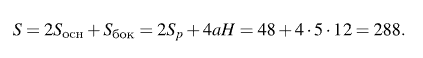

Ответ: 288.

Пермь - 2022