Обязан поставить незачёт неудовл оценку
 Скачать 19.34 Kb.
|
|
КАФЕДРА ТВ И ПМ ДЛЯ СЛУЖЕБНОГО ПОЛЬЗОВАНИЯ НА КАФЕДРЕ Преподаватель обязан поставить незачёт (неудовл. оценку), если студент не знает даже один из перечисленного ниже перечня вопросов. Какие значения может принимать вероятность? Математическое ожидание? Дисперсия? Вероятность наступления события принимает действительное значение из промежутка [0; 1] Средневзвешенная величина всех возможных значений, которые может принимать эта случайная величина. Неотрицательная если КОНСТАНТА то ее десперсия = 0 Что характеризуют параметры распределения МХ, DX, 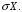 МХ - Математи́ческое ожида́ние (мера среднего значения случайной величины в теории вероятностей) DX – Вероятность (степень возможности наступления некоторого события) oX – Дисперсия (Мера разброса значений случайной величины относительно её математического ожидания.) Формулы для вычисления МХ, DX, 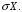(для непрерывного и дискретного случая) .Формулы для DX , DX = М(Х — MX)2 — формула по определению DX — мера рассеяния Определение и вид графика (для непрерывного и дискретного случая) функции распределения. Функция, характеризующая распределение случайной величины или случайного вектора Условие нормировки плотности распределения вероятностей (с объяснением смысла). Вероятность того что случайная величина X жет принять хотя бы какое нибудь значение (из всех возможных) равна ЕДЕНИЦЫ ( 1 ) По интервалу всех возможных значений X Коэффициент корреляции равен 0.9 (0.5; 0,1; -0.7; -1). Что можно сказать про случайные величины X и Y? Вид плотности нормального распределения. Также называемое распределением Гаусса которое в одномерном случае задаётся функцией плотности вероятности совпадающей с функцией Гаусса Почему закон Гаусса называют нормальным? Большинство событий происходят именно с вероятностью нормального распределения например, что когда Вы видите на упаковке хлеба обозначение «Вес: 400±16г» — вес батона имеет нормальное распределение со средним значением 400г и стандартным отклонением 16г. В чём смысл закона больших чисел? Гарантирует устойчивость для средних значений некоторых случайных событий Вероятность попадания в интервал для случайной величины, распределённой по нормальному закону Какие задачи решает математическая статистика? Касаются вопросов обработки наблюдений над массовыми случайными явлениями в зависимости от разных факторов может принимать разную форму (практического вопроса и от объема имеющегося экспериментального материала) Что является оценкой МХ, DX, Что является оценкой функции распределения и плотности |