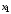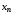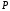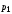Лабораторная работа 1_Модел_случ.чисел. Лабораторная работа 1 Моделирование случайных чисел и событий
 Скачать 283.41 Kb. Скачать 283.41 Kb.
|
Лабораторная работа №1Моделирование случайных чисел и событийМоделирование случайных чисел в среде табличного процессора может быть выполнено двумя способами: с помощью встроенных функций и путем использовании инструмента «Генератор случайных чисел» дополнения «Анализ данных». Так же существуют способы моделирования случайных чисел и событий с использованием встроенных функций. Моделирование простого события Рассмотрим механизм моделирования простого события. Пусть имеется событие 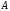 , вероятность наступления которого равна , вероятность наступления которого равна  . Выберем с помощью датчика случайных чисел, равномерно распределенных в интервале (0,1) некоторое число . Выберем с помощью датчика случайных чисел, равномерно распределенных в интервале (0,1) некоторое число  . Известно, что вероятность попадания в интервал (0, . Известно, что вероятность попадания в интервал (0, ) случайной величины ) случайной величины  равна величине равна величине  . Поэтому если при розыгрыше число . Поэтому если при розыгрыше число  попало в этот интервал, то следует считать, что событие попало в этот интервал, то следует считать, что событие 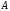 произошло. Противоположное событие (не произошло. Противоположное событие (не 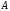 ) произойдет с вероятностью (1 – ) произойдет с вероятностью (1 – ) в том случае, если ) в том случае, если 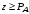 . .Процедура моделирования простого события в имитационной модели описывается алгоритмом, схема которого показана на рис. 1 [23]. Оператор 1 обращается к датчику случайных чисел, генерирующему случайную величину  . Оператор 2 проверяет условие . Оператор 2 проверяет условие . Если оно выполняется, считается, что произошло событие . Если оно выполняется, считается, что произошло событие 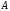 . В противном случае считается, что произошло противоположное событие (не . В противном случае считается, что произошло противоположное событие (не 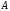 ). ).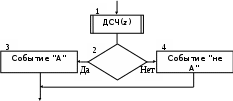 Рис.1 – Моделирование простого события Задание 1: Реализовать в среде табличного процессора данную операцию Моделирование полной группы несовместных событий Пусть имеется полная группа несовместных событий  с вероятностями с вероятностями  . При этом выполняется условие . При этом выполняется условие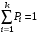 . .Процедура моделирования полной группы несовместных событий описывается алгоритмом, схема которого показана на рис. 2. Здесь  - кумулятивная вероятность - кумулятивная вероятность  . . Рис. 2 – Алгоритм моделирования полной группы несовместных событий Оператор 1 обращается к датчику случайных чисел с равномерным распределением в интервале (0,1). Условный оператор 1 проверяет условие попадания случайной величины  в интервал (0, в интервал (0, ). Если это условие выполняется, то считается, что произошло событие ). Если это условие выполняется, то считается, что произошло событие  . Если условие в операторе 2 не выполняется, то алгоритм осуществляет проверку условий попадания случайной величины в другие интервалы. Одно из событий . Если условие в операторе 2 не выполняется, то алгоритм осуществляет проверку условий попадания случайной величины в другие интервалы. Одно из событий  обязательно произойдет. обязательно произойдет.Задание 2 Выполнить данные операции в среде табличного процессора. Для этого записать в ячейки С2:С4 значения вероятностей  событий событий 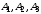 (рис.3). (рис.3). В ячейке С5 смоделировать случайную величину, распределенную равномерно на интервале (0,1). В С6 смоделировать определение произошедшего события 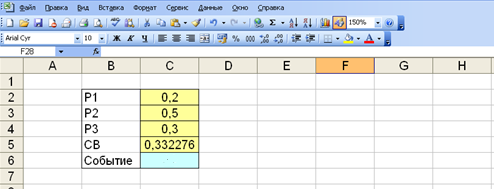 Рис. 3 – Моделирование полной группы несовместных событий Моделирование дискретной случайной величины Дискретная случайная величина может быть задана табличной зависимостью:
Здесь 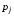 – вероятность того, что дискретная случайная величина – вероятность того, что дискретная случайная величина  примет значение примет значение  . При этом . При этом 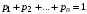 . Разделим интервал (0,1) на . Разделим интервал (0,1) на  отрезков, длины которых равны заданным вероятностям. Если случайное число отрезков, длины которых равны заданным вероятностям. Если случайное число  , вырабатываемое датчиком случайных чисел, равномерно распределенных в интервале (0,1), попадет в интервал , вырабатываемое датчиком случайных чисел, равномерно распределенных в интервале (0,1), попадет в интервал  , то случайная величина , то случайная величина  примет значение примет значение 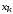 . Таким образом, при моделировании дискретных случайных величин фактически используется та же процедура, что и при моделировании полной группы несовместных событий. . Таким образом, при моделировании дискретных случайных величин фактически используется та же процедура, что и при моделировании полной группы несовместных событий.Моделирование непрерывной случайной величины Задание 3. Выполнить способы моделирования Приведем способы моделирования непрерывных случайных чисел (на рис. 4 показаны формы распределения вероятностей) [23-24]. Показательное распределение  , ,где  - случайная величина, распределенная по показательному закону; - случайная величина, распределенная по показательному закону; - интенсивность потока (среднее значение - интенсивность потока (среднее значение  ); ); - случайная величина, равномерно распределенная на интервале (0,1). - случайная величина, равномерно распределенная на интервале (0,1).В Excel данное вычисление выглядит следующим образом (пусть в ячейке А1 дано среднее значение, а в А2 - результат) А2=-А1*LN(СЛЧИС()). Равномерное распределение на интервале (  ) ) , ,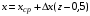 , ,где  - случайная величина, распределенная по равномерному закону; - случайная величина, распределенная по равномерному закону; и и 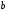 - нижняя и верхняя границы интервала ( - нижняя и верхняя границы интервала ( ) соответственно; ) соответственно; - среднее значение интервала ( - среднее значение интервала ( ); ); - величина интервала ( - величина интервала ( ); ); - случайная величина, равномерно распределенная на интервале (0,1). - случайная величина, равномерно распределенная на интервале (0,1).В Excel это реализуется посредством формулы (пусть в ячейке А1 дана нижняя граница; в ячейке А2 – верхняя граница, а в А3 - результат) А3=А1+СЛЧИС()*(А2-А1) Нормальное распределение Процедура розыгрыша нормально распределенной случайной величины заключается в следующем. Сложим 12 случайных величин 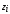 с равномерным распределением в интервале (0,1), т. е. составим сумму с равномерным распределением в интервале (0,1), т. е. составим сумму 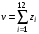 . .Нормируем и центрируем случайную величину  , т. е. перейдем к величине , т. е. перейдем к величине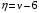 . .От нормированной и центрированной величины  перейдем к случайной величине перейдем к случайной величине  , распределенной по нормальному закону, с заданными параметрами , распределенной по нормальному закону, с заданными параметрами  и и  по формуле по формуле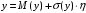 , ,где  – известное математическое ожидание случайной величины – известное математическое ожидание случайной величины  ; ;  – известное среднее квадратическое отклонение случайной величины – известное среднее квадратическое отклонение случайной величины  . .Для реализации данного генератора в среде табличного процессора нужно выполнить следующий расчет (в ячейке А1 дано среднее значение, А2 – среднее квадратическое отклонение, а в А3 - результат) А3=А1+А2*((СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС())-6)).  Рис. 4 – Графики законов распределения Отчет по лабораторной работе №1 Для защиты лабораторной работы необходимо создать: а) отчет (файл «Отчет_Иванов_лаб_1») о проделанной работе в соответствии с требованиями http://www.osu.ru/docs/official/standart/standart_101-2015.pdf, с описанием последовательности действий по каждому заданию. б) Файл xls («Модель_Иванов_лаб_1»), в который включаются выполненные задания 1, 2 и 3 2. Файлы «Отчет_Иванов_лаб_1» и («Модель_Иванов_лаб_1» сдать на проверку в системе Moodle. |