КиТГ. китг. Является бинарным отношением, т к. возвращает в случае верности неравенства единицу и ноль в противном случае

• Название: Является бинарным отношением, т к. возвращает в случае верности неравенства единицу и ноль в противном случае
• Дата: 04.12.2022
• Размер: 65.24 Kb.
• Имя файла: китг.docx
• Тип: Документы; #826673

Демидов М. А.

Гр. 1363

Вариант 10

ИДЗ №1



Функция №1



Является бинарным отношением, т.к. возвращает в случае верности неравенства единицу и ноль в противном случае.

1. Проверка рефлексивности, симметричности и транзитивности:

1. 
   F (x, x): (x – z)*(x – z) < 0 => (x-z)² < 0
   

Но (x-z)² ≥ 0 => F (x, x) = 0 => Не рефлексивно;

2. 
   Арефлексивно, т.к. не рефлексивно;
   
3. 
   Фиксируем a, b ∈ M, ∃z ∈ M: (a – z)*(b – z) < 0 => F (a, b) = 1
   

Из коммутативности умножения натуральных чисел следует:

(b – z)*(a – z) < 0 => F (b, a) = 1
Значит, симметрично;

4. 
   Не асимметрично, т.к. симметрично;
   
5. 
   Не антисимметрично, т.к. симметрично;
   
6. 
   Не транзитивно. Контрпример:
   

(97 – 61)*(56 ­– 61) < 0

(56 – 61)*(88 – 61) < 0

Но (97 – 61)*(88 – 61) > 0.

2. Матрица и граф:

0	97	15	17	20	56	88	61	30
97
15
17
20
56
88
61
30

3. Проверка на отношение эквивалентности, частичного порядка и т.д:

Не рефлексивно => не отношение эквивалентности;

Не рефлексивно => не частичный порядок;

Не частичный порядок => не линейный порядок;

Не асимметрично и не транзитивно => не строгий порядок.

4. Не отношение эквивалентности;

5. Не отношение частичного порядка;

6. Алгоритм Уоршелла:

Функция №2



Является бинарным отношением, т.к. возвращает в случае верности неравенства единицу и ноль в противном случае. Для натуральных чисел определена операция сравнения как бинарная операция.

1. 
   Проверка рефлексивности, симметричности и транзитивности:
   

1. 
   Рефлексивно, т.к. x ≥ x поразрядно => F (x, x);
   
2. 
   Не арефлексивно, т.к. рефлексивно;
   
3. 
   Не симметрично: F (97, 15) = 1, т.к. 97 ≥ 15 поразрядно, но F (15, 97) = 0;
   
4. 
   Не асимметрично, т.к. рефлексивно;
   
5. 
   Антисимметрично, т.к. ∀ a, b ∈ M: F (a, b) =1 и F (b, a) = 1 => a = b;
   
6. 
   Транзитивно, т.к. ∀ a, b, c ∈ M: если a ≥ b поразрядно и b ≥ c поразрядно, то a ≥ c поразрядно.
   

2. 
   Матрица и граф:
   

0	97	15	17	20	56	88	61	30
97	1	1	1	1	1	0	1	1
15	0	1	0	0	0	0	0	0
17	0	1	1	0	0	0	0	0
20	0	0	0	1	0	0	0	0
56	0	1	0	1	1	0	0	1
88	0	1	1	1	1	1	1	1
61	0	0	0	1	0	0	1	1
30	0	0	0	0	0	0	0	1

3. 
   Проверка на отношение эквивалентности, частичного порядка и т.д:
   

Не симметрично => не отношение эквивалентности;

Не асимметрично => не строгий порядок;

Рефлексивно, транзитивно и антисимметрично => частичный порядок;

∃ 65 и 81: F (65, 81) = 0 и F (81, 65) = 0 => не линейный порядок.

4. 
   Не отношение эквивалентности;
   
5. 
   
   
6. 
   Транзитивно.
   

Функция №3



Является бинарным отношением, т.к. операция сравнения определена для натуральных чисел.

1. 
   Проверка рефлексивности, симметричности и транзитивности:
   

1. 
   Рефлексивно, т.к. [x/5] = [x/5] => F (x, x) = 1;
   
2. 
   Не арефлексивно, т.к. рефлексивно;
   
3. 
   Симметрично, исходя из симметричности равенства целых чисел;
   
4. 
   Не асимметрично, т.к. симметрично;
   
5. 
   Не антисимметрично, т.к. симметрично;
   
6. 
   Транзитивно, исходя из транзитивности равенства целых чисел.
   

2. 
   Матрица и граф:
   

0	97	15	17	20	56	88	61	30
97	1	0	0	0	0	0	0	0
15	0	1	1	0	0	0	0	0
17	0	1	1	0	0	0	0	0
20	0	0	0	1	0	0	0	0
56	0	0	0	0	1	0	0	0
88	0	0	0	0	0	1	0	0
61	0	0	0	0	0	0	1	0
30	0	0	0	0	0	0	0	1

3. 
   Проверка на отношение эквивалентности, частичного порядка и т.д:
   

Рефлексивно, транзитивно, симметрично => отношение эквивалентности;

Не антисимметрично => не частичный порядок;

Не частичный порядок => не линейный порядок;

Не асимметрично => не строгий порядок.

4. 
   Построение классов эквивалентности: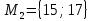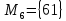
   

5. 
   Не отношение частичного порядка;
   
6. 
   Транзитивно.
   

Функция №4



Является бинарным отношением, т.к. целые числа, получаемые в результате разности, могут быть либо четными, либо нечетными.

1. 
   Проверка рефлексивности, симметричности и транзитивности:
   

1. 
   Проверка рефлексивности на данном множестве:
   

F (97, 97): 97³ – 97³ = –903264 — четное => F (97, 97) = 0;

F (15, 15): 15² – 15³ = –3150 — четное => F (15, 15) = 0;

F (17, 17): 17² – 17³ = –4624 — четное => F (17, 17) = 0;

F (20, 20): 20² – 20³ = –7600 — четное => F (20, 20) = 0;

F (56, 56): 56² – 56³ = –172480 — четное => F (56, 56) = 0;

F (88, 88): 88² – 88³ = –673 728 — четное => F (88, 88) = 0;

F (61, 61): 61² – 61³ = –223 260 — четное => F (61, 61) = 0;

F (30, 30): 30² – 30³ = –26 100 — четное => F (30, 30) = 0;

Отношение не рефлексивно.

2. 
   Арефлексивно, т.к. не рефлексивно;
   
3. 
   Не антисимметрично. Контрпример:
   

F (97, 20): 97² – 20³ = 1 409— нечетно => F = 1

F (20, 97): 20² – 97³ = -912 273 — четно => F = 1

4. 
   Не асимметрично. Контрпример: F (97, 20) = 0 и F (20, 97) = 0;
   
5. 
   Если четное число умножить на четное, то в результате получится четное число. Если из четного числа вычесть четное число, то получится четное число.
   Если нечетное число умножить на нечетное, то получится нечетное число. Если из нечетного числа вычесть нечетное, то будет четное число.
   Если из нечетного числа вычесть четное число, то получится нечетное число. Если из четного числа вычесть нечетное число, то получится нечетное.
   Значит, для a, b ∈ M: F (a, b) = 1  a и b либо одновременно четные, либо одновременно нечетные. И если поменять аргументы данного бинарного отношения местами, четность не изменится.
   

F (a, b) = 1  a² – b³ — четное

F (b, a) = 1  b² – a³ — четное

Значит, бинарное отношение симметрично

6. 
   Транзитивно, т.к. ∀ a, b, c ∈ M: F (a, b) = 1  a и b либо одновременно четные, либо одновременно нечетные. F (b, c) = 1  четность b совпадает с четностью c. Поскольку четность b совпадает с четностью a, то и четность c совпадает с четностью a.
   

Значит если F (a, b) = 1 и F (b, c) = 1, то F (a, c) =1.

2. 
   Матрица и граф:
   

0	97	15	17	20	56	88	61	30
97	0	0	0	1	1	1	0	1
15	0	0	0	1	1	1	0	1
17	0	0	0	1	1	1	0	1
20	1	1	1	0	0	0	1	0
56	1	1	1	0	0	0	1	0
88	1	1	1	0	0	0	1	0
61	0	0	0	1	1	1	0	1
30	1	1	1	0	0	0	1	0

3. 
   Проверка на отношение эквивалентности, частичного порядка и т.д:
   

Не рефлексивно, симметрично, транзитивно => не отношение эквивалентности

Не антисимметрично => не частичный порядок

Не асимметрично => не строгий порядок

Не частный порядок => не линейный порядок

4. 
   Не отношение эквивалентности
   
5. 
   Не отношение частичного порядка;
   
6. 
   Транзитивно.
   

Функция №5



Является бинарным отношением, операция взятия модуля и сравнения определена для целых чисел.

1. 
   Проверка рефлексивности, симметричности и транзитивности:
   

1. 
   Рефлексивно, т.к. ∀ x ∈ M: F (x, x): |x-x| < 10 => 0 < 10 — верно => F (x, x) = 1;
   
2. 
   Не арефлексивно, т.к. рефлексивно;
   
3. 
   Симметрично, т.к. ∀ x, y ∈ M: |x – y| = |y – x|;
   
4. 
   Не асимметрично, т.к. симметрично;
   
5. 
   Не антисимметрично, т.к. симметрично;
   
6. 
   Транзитивно.
   

Матрица и граф:

0	97	15	17	20	56	88	61	30
97	1	0	0	0	0	1	0	0
15	0	1	1	1	0	0	0	0
17	0	1	1	1	0	0	0	0
20	0	1	1	1	0	0	0	0
56	0	0	0	0	1	0	1	0
88	1	0	0	0	0	1	0	0
61	0	0	0	0	1	0	1	0
30	0	0	0	0	0	0	0	1

2. 
   Проверка на отношение эквивалентности, частичного порядка и т.д:
   

Не транзитивно => не частичный порядок

Не частичный порядок => не линейный порядок

Не транзитивно => не строгий порядок

Не транзитивно => не отношение эквивалентности

3. 
   Не отношение эквивалентности;
   
4. 
   Не частичный порядок;
   
5. 
   Транзитивно.