5 лабораторная Хасанов Х.А.. Оценка динамики явления
 Скачать 55.69 Kb. Скачать 55.69 Kb.
|
|
Лабораторная работа №5 Хасанов Х.А. 19лл3 Вариант 15 Тема : Оценка динамики явления. Задание 1. Определите абсолютный прирост, темпы роста и прироста, показатели наглядности.
Вывод: показатель случаев на 100 работающих увеличился на 6 пунктов с 1995 до 2000, по динамике показателей, они увеличивались с 1995 по 1997, в 1998 наблюдали упадок, а затем снова рост по 2000 год Задание 2. Показатели состояния здоровья детей, поступающих в первый класс, по результатам заключительной диспансеризации, характеризовались данными представленными в таблице. Проведите выравнивание ряда по способу наименьших квадратов, фактические и выравненные данные представьте графически. Сделайте вывод.
A=1057,7/12=88,14 B= -699.7/572=-1.223 при х=13 y2002= 74,24 при х=15 y2003= 69,8 при х=17 y2004= 67,36 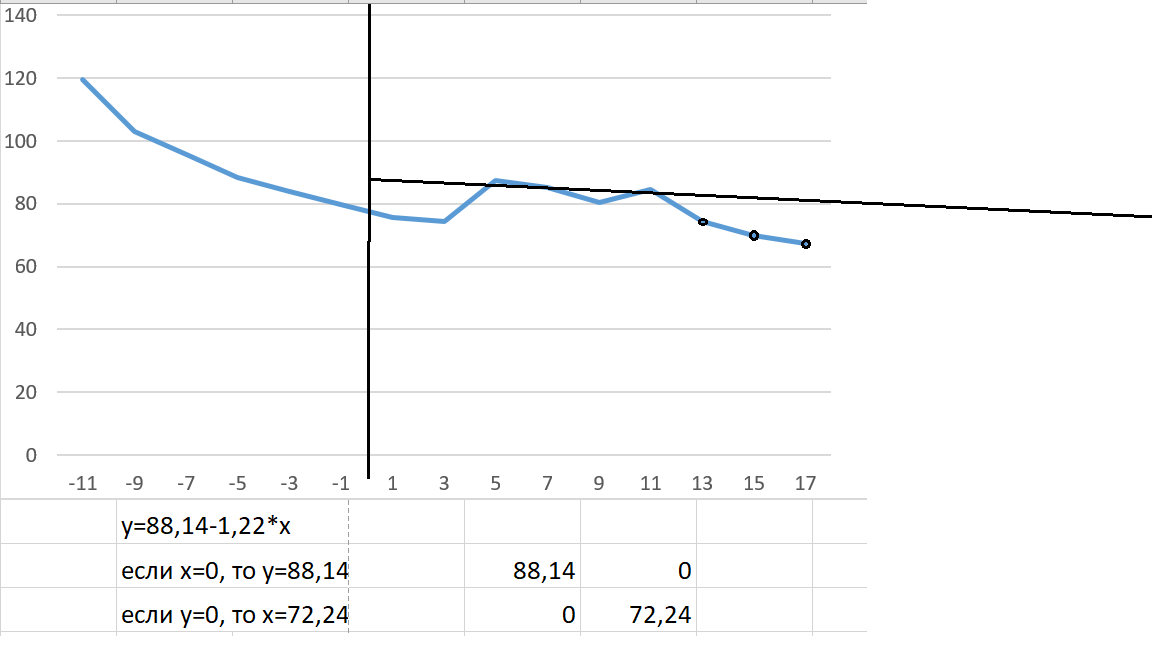 После проведённого выравнивания по способу наименьших квадратов наметилась отчётливая тенденция на уменьшение данного явления на 1000 детей, по результатам диспансеризации. Прогноз на 2002 год – 74,24 человек, на 2003 год – 69,8 человек, на 2004 год – 67,36 человек. Задание 3. Оцените и проанализируйте сезонность заболеваемости по индексам сезонности.
Удельный вес заболеваемости вызванной влиянием сезонных факторов A-число заболеваний за год B -число заболеваний за период сезонного подъема m-число месяцев сезонного подъема S-удельный вес заболеваемости B (A B)*m S12m *100% A Месяцы с индексом сезонности = или больше 100, всего 6 месяцев Сумма заболеваний в месяцы с индексом сезонности больше 100= 25+25+26+26+28+26=156 S=(156-(291-156)*6)/((12-6)/291)*100=7.2% Вывод: S меньше 12, сезонный фактор не влияет на рост заболеваемости. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
