Главная страница
Навигация по странице:

  • Функция трудоемкости алгоритма (для лучшего и худшего случаев)

  • Результаты асимптотический анализ временной эффективности алгоритма

    		•

    Совместная. Оценка правильности и эффективности алгоритмов


    Скачать 86.39 Kb.
    НазваниеОценка правильности и эффективности алгоритмов
    Дата15.05.2023
    Размер86.39 Kb.
    Формат файлаdocx
    Имя файлаСовместная.docx
    ТипДокументы
    #1132527

    «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

    Индивидуальное задание №1

    "Оценка правильности и эффективности алгоритмов"

    Выполнил студент группы №0721

    Поречин П.С

    Проверил преподаватель

    Егорова О.В

    Томск-2023

    Задание


    1. Провести тестирование алгоритма методами черного и белого ящиков.

    2. Провести теоретическое доказательство правильности алгоритма с использованием наиболее подходящих аналитических методов (перечисления вариантов, индукции, и т.п.).

    3. Получить функцию трудоемкости для лучшего и худшего случаев.

    Провести асимптотический анализ временной эффективности алгоритма (оценить порядок роста функции трудоемкости при бесконечно большом размере входных данных) в O, , - обозначениях. Определить класс сложности анализируемого алгоритма в O-обозначении.

    Формулировка задания из лабораторной работы №3:

    Дан действительный массив максимальной размерности 20*20. Найти элемент с наибольшим значением из тех, которые расположены в заштрихованной части области, определить его номер. В случае, если в выделенной области имеется несколько элементов с таким значением, также определить их номера. Ввод исходного массива организовать с терминала, при вводе учесть возможность ввода массива меньшей размерности. Вывести в файл и на экран исходный массив, преобразованный массив и найденные элементы и их номера.

    Алгоритм решения задания лабораторной работы №3


    Код программы:

    #include

    #include

    int main ()

    {

        char ch;

        int i, j, n, m, z, num0, num1,  key;

        float g[20][20];

        do{

            z=5;

            num0=0;

            num1=0;

        FILE *f = fopen("massiv.txt","w");

        do

        {  

            printf("Введите количество строк массива: ");

            scanf("%d", &n);

            if (n<1 || n>20) printf("Вы превысели лимит доступных строк 20 на 20. Осталось попыток %d\n",z);

                z--;

            if (z==0)

                {

                    printf("Превышен лимит попыток!\n");

                    return 0;

                }

        } while (n<1 || n>20);

       do

        {

            printf("Введите количество столбцов массива: ");

            scanf("%d", &m);

            if (m<1 || m>20) printf("Вы превысели лимит доступных столбцов 20 на 20.Осталось попыток %d\n",z);

                z--;

            if (z==0)

                {

                    printf("Превышен лимит попыток!\n");

                    return 0;

                }

        } while (m<1 || m>20);

        printf("Выберите способ заполения массива.\nВведите 1 для ручного заполнения или введите 2 для генерации псевдо случайными числами:");

        scanf("%d",&key);

        if (key==1)

        {

            printf("Введите элементы массива\n");

            for (i = 0; i < n; i++)

            {

                for (j = 0; j < m; j++)

                {

                printf("[%d] [%d]: ", i, j);

                scanf("%f",&g[i][j]);// ввод элеметов массива при j < m в терминале

                }

                fprintf(f, "\n");

                printf("\n");

            }

        }

        else if (key==2)

        {

        for (int i = 0; i < n; i++)

        {

            for (int j = 0; j < m; j++)

            {

                g[i][j] = rand() % 100;

                printf("%.1f\t", g[i][j]); //заполнение элеменатами массива строки при j < m в терминале

                fprintf(f, "%.1f\t", g[i][j]);//заполнение элеменатами массива строки при j < m в файле

            }

            fprintf(f, "\n");//переход на новую строку в файле при j > m

            printf("\n");//переход на новую строку в терминале при j > m

        }

        }

        else

        {

            printf("Ошибка выбора действий !\n");

            getchar();

            return 0;

        }

        printf("\n\n");

        fprintf(f, "\n\n");

        float max = g[0][0];

        for (int i = 0, k = m - 1, t = m - 1; i < n; i++, k--)

        {

            for (int j = 0; j < m; j++, t--)

            {

                if (i == t || (j >= i && j >= k) || (j <= i && j <= k))

                {

                    if (g[i][j] > max)

                    {

                        max = g[i][j];

                        num0=i;

                        num1=j;

                    }

                    printf("%.1f\t", g[i][j]);

                    fprintf(f, "%.1f\t", g[i][j]);

                }

                else

                {

                    printf("*\t");

                    fprintf(f, "*\t");

                }

            }

            t=m-1;

            printf("\n");

            fprintf(f,"\n");

        }

        printf("max[%d][%d] = %.1f\n", num0+1, num1+1, max);

        fprintf(f,"max[%d][%d] = %.1f\n", num0+1, num1+1, max);

        fclose(f);

        printf("Хотите запустить программу снова ? (Y/N)\n");

        scanf(" %c",&ch);

        }while(ch=='Y' || ch=='y');

        return 0;

    }

    Результаты тестирования методом черного ящика


    Тестирование данным методом можно осуществить способом эквивалентного разбиения. Для тестирования данным методом определяем различные классы эквивалентности входных данных и их ожидаемый результат.

    В данном случае, программа запрашивает у пользователя количество строк и столбцов массива, а затем заполняет его либо псевдослучайными числами, либо вручную. Затем программа находит максимальный элемент в определенной части массива и выводит его координаты и значение.

    Можно провести тестирование программы на основе следующих критериев:

    1. Ввод корректных данных:

    - Ввод числа строк и столбцов в пределах от 1 до 20;

    - Выбор способа заполнения массива (1 или 2);

    - Ввод элементов массива вручную (если выбран способ 1);

    - Генерация псевдослучайных чисел (если выбран способ 2);

    - Ввод символа Y для повторного запуска программы.
    2. Ввод некорректных данных:

    - Ввод числа строк и столбцов меньше 1 или больше 20;

    - Ввод значения, не являющегося числом, при вводе элементов массива вручную;

    - Ввод значения, не являющегося 1 или 2, при выборе способа заполнения массива;

    - Ввод значения, не являющегося Y, при запросе на повторный запуск программы.
    3. Проверка правильности работы программы:

    - Проверка нахождения максимального элемента в заданной части массива;

    - Проверка вывода координат и значения максимального элемента.
    Примеры данных для всех 3-й сценариев:

    1. Ввод корректных данных:

    - Ввод числа строк и столбцов: 5, 5;

    - Выбор способа заполнения массива: 1;

    - Ввод элементов массива вручную;

    - Ввод символа Y для повторного запуска программы.
    Ожидаемый результат: программа завершается без ошибок.
    2. Ввод некорректных данных:

    - Ввод числа строк и столбцов: -1, 30;

    - Ввод значения, не являющегося числом, при вводе элементов массива вручную;

    - Ввод значения, не являющегося 1 или 2, при выборе способа заполнения массива;

    - Ввод значения, не являющегося Y, при запросе на повторный запуск программы.
    Ожидаемый результат: программа выдает сообщение об ошибке и запрашивает корректный ввод.
    3. Проверка правильности работы программы:

    - Ввод числа строк и столбцов: 4, 4;

    - Выбор способа заполнения массива: 2;

    - Генерация псевдослучайных чисел;

    - Проверка вывода координат и значения максимального элемента.
    Ожидаемый результат: программа находит максимальный элемент в заданной части массива и выводит его координаты и значение.

    Результаты тестирования методом белого ящика


    Тестирование будем проводить на примере цикла, реализующего поиск максимального элемента и его координат:

    float max = g[0][0];

        for (int i = 0, k = m - 1, t = m - 1; i < n; i++, k--)

        {

            for (int j = 0; j < m; j++, t--)

            {

                if (i == t || (j >= i && j >= k) || (j <= i && j <= k))

                {

                    if (g[i][j] > max)

                    {

                        max = g[i][j];

                        num0=i;

                        num1=j;

                    }

                    printf("%.1f\t", g[i][j]);

                    fprintf(f, "%.1f\t", g[i][j]);

                }

                else

                {

                    printf("*\t");

                    fprintf(f, "*\t");

                }

            }

            t=m-1;

            printf("\n");

            fprintf(f,"\n");

        }

        printf("max[%d][%d] = %.1f\n", num0+1, num1+1, max);

        fprintf(f,"max[%d][%d] = %.1f\n", num0+1, num1+1, max);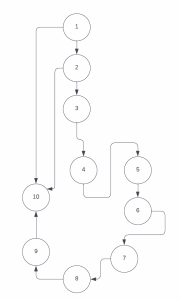



    Рисунок 1. Граф базового пути.


    Поток выполнения алгоритма методом белого ящика на основе потоковых графов:

    1. Поток выполнения, когда n и m равны 0: 1-10.

    Результат: программа завершается без вывода.

    2. Поток выполнения, когда вводятся корректные значения для n и m:

    1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 -10.

    n = 2, m = 2, элементы матрицы g - 1 2 3 4.

    Результат: программа выводит элементы матрицы g и максимальный элемент с его индексами:

    1.0 2.0

    3.0 4.0

    max[2][2] = 4.0

    - n = 3, m = 3, элементы матрицы g - 1 2 3 4 5 6 7 8 9.

    Результат: программа выводит элементы матрицы g и максимальный элемент с его индексами:

    1.0 * 3.0

    4.0 5.0 6.0

    7.0 * 9.0

    max[3][3] = 9.0

    - n = 4, m = 4, элементы матрицы g - 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16.

    Результат: программа выводит элементы матрицы g и максимальный элемент с его индексами:

    1.0 * * 4.0

    5.0 6.0 7.0 8.0

    9.0 10.0 11.0 12.0

    13.0 * * 16.0

    max[4][4] = 16.0

    3. Поток выполнения, когда вводятся некорректные значения для n и m:

    1 - 2 - 10.

    - n = -1, m = -2.

    Результат: программа завершается без вывода.

    - n = 0, m = 5.

    Результат: программа завершается без вывода.

    - n = -1, m = 10.

    Результат: программа завершается без вывода.

    - n = 5, m = 0.

    Результат: программа завершается без вывода.

    Результаты аналитическое доказательство правильности алгоритма


    for (int i = 0, k = m - 1, t = m - 1; i < n; i++, k--)

        {

            for (int j = 0; j < m; j++, t--)

            {

                if (i == t || (j >= i && j >= k) || (j <= i && j <= k))

                {

                    if (g[i][j] > max)

                    {

                        max = g[i][j];

                        num0=i;

                        num1=j;

                    }

                    printf("%.1f\t", g[i][j]);

                    fprintf(f, "%.1f\t", g[i][j]);

                }

                else

                {

                    printf("*\t");

                    fprintf(f, "*\t");

                }

            }

            t=m-1;

            printf("\n");

            fprintf(f,"\n");

        }

        printf("max[%d][%d] = %.1f\n", num0+1, num1+1, max);

        fprintf(f,"max[%d][%d] = %.1f\n", num0+1, num1+1, max);
    Алгоритм находит максимальный элемент в матрице g, который расположен ниже главной или побочной диагонали, или расположен на диагоналях. Для этого происходит перебор всех элементов матрицы, начиная от первого элемента первой строки до последнего элемента последней строки, и проверка условия, удовлетворяет ли текущий элемент матрицы условию для вывода на экран и записи в файл. Если текущий элемент удовлетворяет условию и больше максимального элемента, то он становится новым максимальным элементом.
    Алгоритм правильный, так как он проверяет все элементы матрицы и находит максимальный элемент, который расположен на главной или побочной диагонали. Условие для проверки элемента матрицы на то, что он находится на главной или побочной диагонали, является корректным, так как диагонали матрицы являются линиями, на которой i и j равны, а побочная диагональ матрицы имеет индексы i + j = m - 1.
    Кроме того, алгоритм закончится за конечное число раз, так как он использует два вложенных цикла, которые перебирают все элементы матрицы. Таким образом, количество итераций циклов будет равно произведению n и m, что является конечным числом. Таким образом, алгоритм правильный и будет работать корректно для любой матрицы.
    Функция трудоемкости алгоритма (для лучшего и худшего случаев)

    Алгоритм выполняет одинаковое количество операций при фиксированных значениях n и m, и, следовательно, является количественно-зависимым. Его функция трудоемкости зависит только от размерности конкретного входа.

    for (int i = 0, k = m - 1, t = m - 1; i
    for (int j = 0; j < m; j++, t--) \\ запись j=0, логическая операция j < m, 2 арифметические записи и 2 записи в память j++, t--.

    if (i == t || (j >= i && j >= k) || (j <= i && j <= k)) \\ 9 логических операций.

    if (g[i][j] > max) \\ 1 логическая операция, чтение.

    max = g[i][j] \\ чтение, запись в память.

    num0=i \\ чтение, запись в память.

    num1=j \\ чтение, запись в память.

    t=m-1 \\ запись, арифметическая операция.

    Для лучшего случая: T(n) = 3+(n+1)+6n+n*(1+(n+1)+4n+((n+9)+((n+1)+2n)+2n+2n+2n))+n+2n=6n2+19n+19

    Для худшего случая: T(n) = 3+(n-1)+6n+n*(1+(n-1)+4n+((n-9)+((n-1)+2n)+2n+2n+2n))+n+2n=6n2+19n+13
    Результаты асимптотический анализ временной эффективности алгоритма

    T(n) = f(n) – функция трудоемкости анализируемого алгоритма g(n) –функция, с которой осуществляется сравнение.

    О – обозначение.



    Функция трудоемкости f(n) = 6n2+19n+19 = О(n).

    f(n) ≤ c× g(n) для всех n ≥ n0

    Возьмем С = 7+19/n+100/n2, n0 = 0. Данные значения обеспечивают выполнение неравенства 0 ≤ 6n2+19n+19 ≤ 7n2+19n +100 для любых n ≥ 0.

    Функция g(n)= 7n2+19n +100 проходит выше функции f(n)= 6n2+19n+19, т.е. порядок роста анализируемой функции трудоемкости f(n)= 6n2+19n+19 не выше n2 (рис. 2).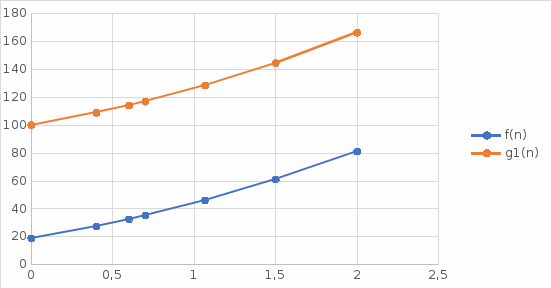



    Рисунок 2. График О – обозначение

    - обозначение


    Функция трудоемкости f(n) = 6n2+19n+19 =n

    f(n) ≤ c× g(n) для всех n ≥ n0

    Возьмем С = 20-25/n+50/n2, n0 = 1.0663. Данные значения обеспечивают выполнение неравенства 0 ≤ 6n2+19n+19 ≤ 20n2-25n+50 для любых n ≥ 1.0663.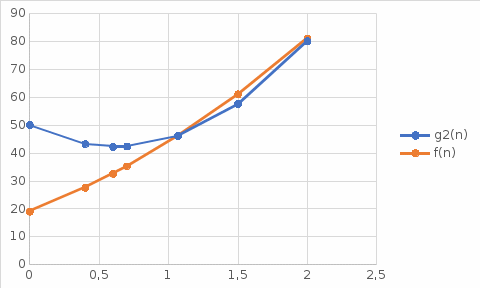


    Рисунок 3. График - обозначения

    обозначение

    Функция трудоемкости f(n) = 6n2+19n+19= n2

    c1 × g(n) ≤ f(n) ≤ c2 × g(n)

    Правая часть неравенства – верхняя граница: возьмем c1 = 7+19/n+100/n2, n0 = 0 , данные значения обеспечивают выполнение неравенства 6n2+19n+19 ≤ 7n2+19n +100 для любых n >= 0.

    Левая часть – нижняя граница: возьмем c2 = 20-25/n+50/n2, n0 = 1.0663, данные значения обеспечивают выполнение неравенства 6n2+19n+19 ≤ 20n2-25n+50 для любых n >= 1.0663.

    Таким образом функция f(n) ограничена сверху и снизу функцией g(n) для любых

    n >= 1.0663, с точностью до постоянных множителей 7+19/n+100/n2 и 20-25/n+50/n2 (рис. 4).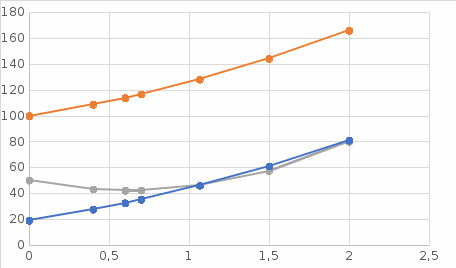



    Рисунок 4. График обозначение (оранжевая – g(n) = 7n2+19n +100, серая – f(n) = 6n2+19n+19, а синяя g(n) =20n2-25n+50)
    Поскольку функция трудоемкости имеет вид квадратичного уравнения T(n) = 6n2+19n+19, можно сделать вывод, что класс сложности алгоритма квадратичный, т.е. О(n2).

    Вывод


    В результате выполнения задания была проведена оценка правильности и эффективности алгоритма, использованного при выполнении лабораторной работы № 3. Тестирования методами белого и черного ящиков, а также аналитическое доказательство правильности алгоритма показали, что задача была решена верно. На основе результата асимптотического анализа временной эффективности алгоритма и оценки трудоемкости алгоритма был определен линейный класс сложности представленного решения.

    написать администратору сайта