Лаба №1мояяяяяя. Оценка точности прямых и косвенных измерений

• Название: Оценка точности прямых и косвенных измерений
• Дата: 26.10.2022
• Размер: 0.56 Mb.
• Имя файла: Лаба №1мояяяяяя.doc
• Тип: Лабораторная работа; #754890

Министерство образования Российской Федерации

Национальный минерально-сырьевой университет «Горный»


Кафедра физики

Лабораторная работа №1

По дисциплине: механика .

(наименование учебной дисциплины согласно учебному плану)

Тема: Оценка точности прямых и косвенных измерений
Выполнила: студентка гр. АПН-12 _________ Малкова Ю.В.



^{(подпись) (Ф.И.О.)}

Дата: 16.09.12

ПРОВЕРИЛ: доцент Тупицкая Н.А.

^{(должность) (подпись) (Ф.И.О.)}
Санкт-Петербург

2012

Цель работы – провести прямые и косвенные измерения физических величин. Сделать оценку точности измерений.

Общие сведения:

R– величина, характеризующая сопротивление проводника электрическому току.

[R] = [Ом] – сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток 1А. Сопротивление зависит от формы, размеров и материала проводника.

Каждую из физических величин – длина проводника, диаметр сечения, напряжение и сила тока( , d, U, I) – прямые измерения (можно измерить непосредственно соответствующими приборами с определенной точностью). Величина удельного сопротивления (ρ) – косвенные измерения (вычисляется при помощи формул).

В общем случае результат измерения величины Х представляют в виде:

,

где погрешность или ошибка измерения; - среднее значение величины.

Для однократных измерений за величину ошибки принимается систематическая погрешность, которую вносит сам прибор, а средним считается измеренное значение физической величины.

Измерение длины проволоки проводится однократно линейкой. Погрешность измерения линейкой определяется как половина цены наименьшего деления.

Значения тока I и напряжения U измеряют однократно с помощью электромагнитных приборов (амперметра и вольтметра) для десяти значений длины . Погрешность и этих измерений определяется по классу точности, который указан на шкале приборов, значению силы тока и напряжения, которые могут быть измерены по шкале прибора.

Диаметр проволоки измеряется многократно штангенциркулем и микрометром. Проведя n измерений, получим результаты: d1, d2, d3,…, dn. Диаметр определяется как среднее арифметическое. Если ошибка меньше точности используемого прибора, то за величину ошибки следует принять последнюю.

Основные расчётные формулы:

Сила тока: [ ]

Сопротивление проводника: [ ],

Удельное сопротивление: [ ] = [Ом∙м]

Среднее значение диаметра:

Графическое вычисление среднего значения удельного сопротивления:

, где

Формулы погрешности:

При прямых измерениях:

Средняя абсолютная ошибка измерений диаметра:

Средняя квадратичная ошибка измерений диаметра:

Абсолютная погрешность прибора: , , где К – класс точности приборов; и - наибольшие значения силы тока и напряжения, которые могут быть измерены по шкале прибора.

При косвенных измерениях:

Средняя абсолютная погрешность измерения сопротивления:



Средняя квадратичная погрешность измерения сопротивления: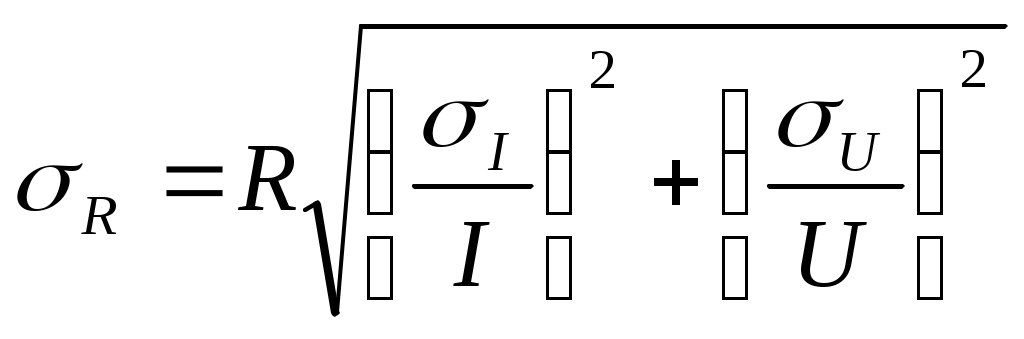



Средняя абсолютная погрешность измерения удельного сопротивления:



Средняя квадратичная погрешность измерения удельного сопротивления: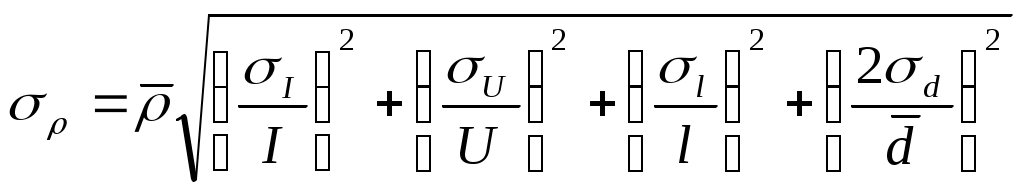


Схема установки: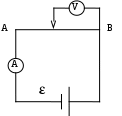


АВ - исследуемый участок

 - источник тока

V – вольтметр

А - амперметр

Таблица 1. Результаты измерений диаметра проволоки штангенциркулем и микрометром

Диаметр	Штангенциркуль	Микрометр
	Размерность
	мм	мм
d1	0,50	0,52
d2	0,48	0,49
d3	0,49	0,49
d4	0,51	0,52
d5	0,52	0,49
d6	0,50	0,52
d7	0,50	0,48
d8	0,48	0,48
d9	0,51	0,49
d10	0,51	0,52
	0,50	0,50
d
d	0,0042	0,0056
	0,02	0,032
	0,0084	0,0112

Таблица 2. Результаты измерений тока и напряжения.

Номер опыта
	м	мм	A	A			Ом	Ом	Ом
1	0,50		0,065		0,29		4,46	0,805	0,5751
2	0,45		0,065		0,27		4,15	0,780	0,5610
3	0,40		0,065		0,25		3,85	0,758	0,5489
4	0,35		0,065		0,23		3,54	0,734	0,5362
5	0,30		0,065		0,20		3,08	0,699	0,5193
6	0,25		0,065		0,18		2,77	0,675	0,5086
7	0,20		0,065		0,16		2,46	0,651	0,4986
8	0,15		0,065		0,14		2,15	0,626	0,4896
9	0,10		0,065		0,12		1,85	0,604	0,4839
10	0,05		0,065		0,10		1,54	0,580	0,4770

Примеры расчетов:






















График зависимости R = f(l).
Таблица данных для графика:

l, м	R, Ом
0,50	4,46
0,45	4,15
0,40	3,85
0,35	3,54
0,30	3,08
0,25	2,77
0,20	2,46
0,15	2,15
0,10	1,85
0,05	1,54

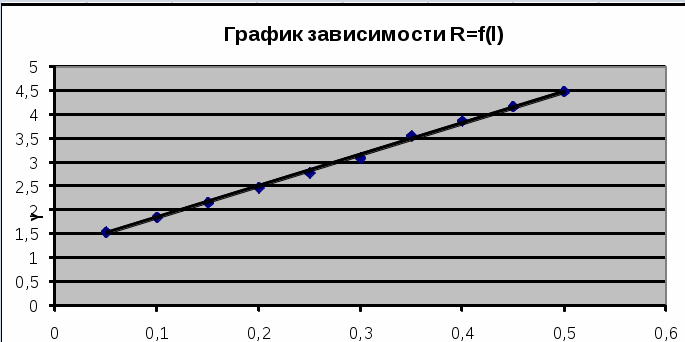Графически среднее значение удельного сопротивления:

, где




Конечные результаты:









Вывод:

В данной лабораторной работе я провела измерения и вычисления, необходимые для определения удельного сопротивления предложенного проводника. Для измерений я использовала штангенциркуль и микрометр, но для уменьшения погрешности, при вычислении были использованы показания штангенциркуля. Результаты получились следующие:









Полученная погрешность имеет небольшое значение, что даёт право говорить об отсутствии грубых ошибок при измерениях и вычислениях. Следуя из всего вышесказанного можно сделать вывод, что данный метод вычисления, при данных приборах можно использовать для определения удельного сопротивления.