Лабораторная работа № 1 Демина. Метрология, стандартизация и сертификация
 Скачать 28.71 Kb. Скачать 28.71 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Ухтинский государственный технический университет» (УГТУ) Кафедра электроэнергетики и метрологии Отчёт по лабораторной работе № 2 «Косвенные измерения и их погрешности» по дисциплине «Метрология, стандартизация и сертификация» Выполнил: обучающаяся гр. ТБ-20з Н.С. Демина шифр 200872 Проверил: К.С. Отев Ухта, 2022 Порядок выполнения работы: 1. Опытным путем были произведены однократные измерения диаметра и высоты двух цилиндров средствами измерений различной точности: штангенциркулем, микрометром и линейкой. 2. Определить средние значения диаметра ͞d высоты цилиндра ͞h 3. Определить усредненный объем цилиндра используя соотношение: 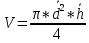 4. Определить абсолютную погрешность каждого измерения диаметра и высоты: Δdi = di - 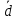 ; Δhi = hi - ; Δhi = hi - 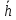 5. Определить усредненную абсолютную погрешность измерения диаметра и высоты: 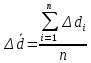 ; ; 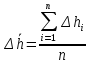 6. Определить относительную погрешность измерения диаметра и высоты, выраженную в относительных единицах: δd = 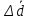 / / 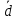 ; δh = ; δh = 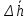 / / 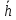 7. Определить относительную погрешность измерений: V = 2d h 8. Определить абсолютную погрешность измерения объема: ΔV= V*V 9. Округлить погрешности измерений и записать результат измерений объемов цилиндров (мм3): V (V V). 10.Заполнить таблицу 1. Таблица 1
Вывод: В данной лабораторной работе мною были произведены измерения и вычисления для определения объёмов цилиндров. В процессе измерений мною были использованы три прибора: микрометр, штангенциркуль и линейка, но наименьшие погрешности, при вычислении были получены штангенциркулем и микрометром. Полученная погрешность имеет небольшое значение, что даёт право говорить об отсутствии грубых ошибок при измерениях и вычислениях. 11.Ответить кратко на контрольные вопросы и представить отчет о выполнении в утвержденной форме. Контрольные вопросы: 1. Назовите основные виды измерений. Ответ: Основными видами измерений физических величин, в том числе и линейно-угловых (ГОСТ 16263–70), являются прямые, косвенные, совокупные, совместные, абсолютные и относительные. 2. По каким признакам классифицируются погрешности измерения? Ответ:- По способу выражения: абсолютная погрешность, относительная погрешность;- По источнику возникновения: инструментальная погрешность, методическая погрешность, субъективная погрешность;- По характеру проявления: случайная погрешность, систематическая погрешность, грубая погрешность;3. Назовите и охарактеризуйте основные виды погрешностей измерений. Ответ: Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины. Относительная погрешность – это число, отражающее степень точности измерения. Это значение вычисляемое как отношение значения абсолютной погрешности к действительному значению измеряемой величины. Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению. 4. Как определить погрешность записи числа? Ответ: Погрешность записи числа определяется как отношение половины единицы младшего разряда числа к значению числа. 5. Как определить погрешность результата косвенного измерения? Ответ: Определить погрешность результата косвенного измерения это определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
