Метрология размеры теория. метрология — копия. Обработка результатов многократных измерений
 Скачать 54.27 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра метрологии, приборостроения и управления качеством Практическая работа на тему «Обработка результатов многократных измерений» Выполнил: студент гр. ПГС-21-1 _____________ Богородский Н.В. (подпись) Проверил: доцент _____________ Радушинский Д.А. (подпись) Санкт-Петербург 2022 Ход работы: Согласно варианту, распределили числа в порядке возрастания. Нашли среднее арифметическое данных измерений Находим разницу между данным значением и ср. арифметическим, полученным в пункте 2. Результат возводим в квадрат, и повторяем для всех измерений. Среднее квадратическое отклонение группы из пункта 3, содержащей 93 результатов измерений, вычисляют по формуле:  Определяем количество интервалов по формуле: 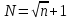 Определяем ширину интервала h по формуле: 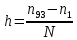 Находим середины интервалов, для этого берем границы интервалов и делим на два. Определяем число результатов измерений в интервале Используя формулы из ГОСТов, заполним таблицу: 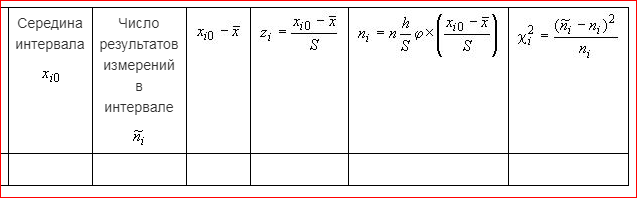 Найдем среднее значение критерия К. ПирсонаНаходим число степеней свободы по формуле f=N-3 Определяем верхнее и нижнее квантили Проводим оценку случайной погрешности. Ср. арифм. и ср. кв. отклонения были получены ранее, доверительную вероятность примем 0.95, коэффициент по Чебышеву равен корень из 20. Получим доверительный интервал, умножим ср. кв. отклонение на коэф. по Чебышеву, получим отклонение по формуле:  Если есть нулевые интервалы, то объединяем соседние интервалы и проводим аналогичные вычисления Построим график теоретического распределения ф. Построим график для фактического распределения ф. Построим гистограмму фактического и теоретического распределения вероятности для каждого случая |