МСС. Оценка условий бурения интервала пористых горных пород, слагающих стенку скважины, по показателям их механических свойств
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра “Бурение нефтяных и газовых скважин” Домашнее задание по курсу «Механика сплошных сред» “ ОЦЕНКА УСЛОВИЙ БУРЕНИЯ ИНТЕРВАЛА ПОРИСТЫХ ГОРНЫХ ПОРОД, СЛАГАЮЩИХ СТЕНКУ СКВАЖИНЫ, ПО ПОКАЗАТЕЛЯМ ИХ МЕХАНИЧЕСКИХ СВОЙСТВ ” Вариант 16-16 Выполнил: студент группы ГБз-19-01 Кузнецов К.К. Проверил: доцент, кандидат техн. наук Трушкин О.Б. Уфа 2022 СОДЕРЖАНИЕ ВВЕДЕНИЕ Целью расчетных домашних заданий является приобретение практических навыков решения технологических задач бурения с использованием знаний, полученных при изучении "Механики сплошных сред". Расчетные задания включают следующие задачи: 1) определение статистических характеристик показателей механических свойств горных пород; 2) расчет естественных давлений и напряжений в горной породе как двухкомпонентной среде, расчет предельной зависимости для горной породы заданного интервала бурения (пласта) по теории прочности Мора-Кулона; 3) обоснование плотности бурового раствора из условий сохранения стенок скважины в упругом состоянии с учетом длительной прочности горной породы, предупреждения притока пластового флюида в скважину и открытия поглощения в результате гидроразрыва пласта. Исходные данные для решения задач: - интервал бурения – 2700-3250 м; - литология интервала (пласта) – алевролиты; - средняя плотность вышележащих горных пород, = 2430 кг/м3; - относительное пластовое давление – p'= 1,06; - ожидаемые колебания давления бурового раствора в скважине рс =3,25 МПа. Задание содержит таблицу показателей механических свойств горной породы в виде вариационных рядов по глубине бурения от кровли до подошвы пласта: - сж = 208 МПа – предел прочности породы при одноосном сжатии; - 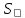 = 27 МПа – среднее квадратичное отклонение предела прочности породы при одноосном сжатии; = 27 МПа – среднее квадратичное отклонение предела прочности породы при одноосном сжатии;- р0 = 670 МПа – предел текучести горной породы по штампу; - 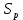 = 26 МПа – среднее квадратичное отклонение предела текучести горной породы по штампу; = 26 МПа – среднее квадратичное отклонение предела текучести горной породы по штампу;- = 0,29 - коэффициент Пуассона; - 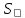 = 0,009 – среднее квадратичное отклонение коэффициента Пуассона; = 0,009 – среднее квадратичное отклонение коэффициента Пуассона;- m = 0,105 – общая пористость горной породы в долях единицы; - 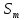 = 0,027 – среднее квадратичное отклонение общей пористости горной породы в долях единицы. = 0,027 – среднее квадратичное отклонение общей пористости горной породы в долях единицы.РАСЧЕТ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПОКАЗАТЕЛЕЙ МЕХАНИЧЕСКИХ СВОЙСТВ ГОРНОЙ ПОРОДЫ В задании приведены показатели механических свойств горной породы интервала, измеренные на образцах, представляющих случайную выборку равномерно распределенную по глубине. Показатели образуют вариационные ряды значений соответствующих случайных величин (показателей свойств). При статистическом анализе данных маловероятные события характеризуются уровнем значимости. Односторонний уровень значимости q может составлять: q = 0,025 – редкие события; q = 0,005 – очень редкие события; q = 0,0005 – чрезвычайно редкие события. В бурении уровень значимости принимается 0,025. В ответственных случаях уровень значимости может быть принят равным 0,005, т. к. он характеризует “меру риска”, с которым принимается то или иное техническое или технологическое решение. Определение нижней xн и верхней хв границ показателей свойств горной породы: 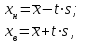 где t – параметр распределения Стьюдента при принятой вероятности 0,95. Принимаем t = 2,06 σсж: 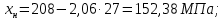 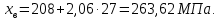 р0: 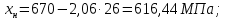 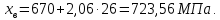 μ: 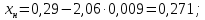 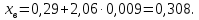 m: 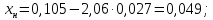 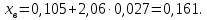 Заполненная таблица является основным результатом статистической обработки измерений показателей механических свойств горной породы и содержит исходные данные для дальнейших расчетов. Таблица 1 - Статистические характеристики показателей механических свойств горных пород
РАСЧЕТ СТЕНОК СКВАЖИНЫ НА ПРОЧНОСТЬ τmax < τs 1. Расчет предельной зависимости Мора-Кулона В соответствии с теорией прочности Мора-Кулона предел текучести материала зависит от среднего нормального напряжения. Для горных пород эту зависимость принимаем в виде τs = τ0 +Ā·σср, где τ0 – начальная ордината (сцепление горной породы); σср- среднее нормальное напряжение в скелете горной породы; Ā – коэффициент пропорциональности. Параметры Ā и τ0 можно определить на основании испытаний горных пород на одноосное сжатие и вдавливание штампа: при одноосном сжатии  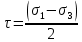 , , 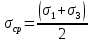 Одноосное сжатие: σ1=0; σ3= σсж τs = σсж /2; σср = σсж /2; при вдавливании штампа: τs = k1·p0; σср = k2·p0, где k1 и k2 – коэффициенты пропорциональности, зависящие от коэффициента Пуассона: k1 = 0,348 – 0,114 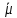 = 0,348-0,114·0,29=0,315; = 0,348-0,114·0,29=0,315; k2 = 0,509 + 0,020 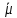 = 0,509+0,020·0,29 = 0,515. = 0,509+0,020·0,29 = 0,515.При испытании на одноосное сжатие и вдавливание штампа принимаем рп = 0. Тогда для определения параметра Ā получим систему, 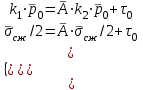 решение которой относительно Ā следующее: Ā = (k1·p0 – 0,5сж )/(k2p0 – 0,5сж) = (0,315·670 – 0,5·208)/(0,515·670–0,5·208) = 0,444. Возможность выхода стенки скважины из упругого состояния тем выше, чем меньше прочность породы и чем выше коэффициент Пуассона. Поэтому параметр 0 определяется по показателям р0н, сж.н. Тогда: 0 = (k1–Ā·k2 )p0н = (0,315–0,444·0,515)·616,44 = 53,22 МПа; τ0″ = (1–Ā)0,5σсж.н = (1–0,444) ∙0,5·152,38 = 42,36 МПа. Из двух значений 0, рассчитанных по формулам, выбираем меньшее. Итогом расчета будет уравнение, записанное с числовыми коэффициентами Ā = 0,444 и 0 = 42,36 МПа s = 0,444ср + 42,36, МПа, которое и будет характеризовать прочностные свойства горной породы заданного интервала бурения. 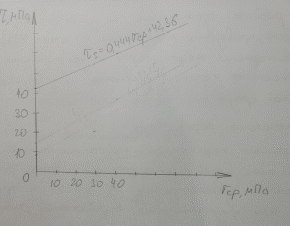 2. Расчёт естественных давлений и напряжений в горных породах Естественные напряжения в горных породах обусловлены весом вышележащих пород и пластовым давлением рп. Осредненные напряжения в горной породе называются горным давлением и характеризуются двумя компонентами: геостатическим рг и боковым рб давлениями (рис. 2.1). Геостатическое давление равно: рг = ρ·g·z = 2430·9,81·3250 = 77,47 МПа, где ρ – плотность горных пород по заданию; g – ускорение свободного падения; z – глубина залегания пород по подошве заданного интервала. 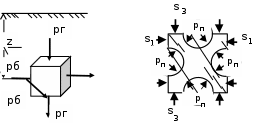 а) б) Рис. 2.1 – Схемы к расчету компонент горного давления (а) и напряжений в скелете горной породы (б) Характеристикой бокового давления является коэффициент бокового распора λ, значения которого с заданной вероятностью лежат в интервале от λн до λв: λн = μн /(1 – μн)=0,271/(1-0,271)=0,372; λв = μв /(1 – μв)=0,308/(1-0,308)=0,445; Давление жидкостей и газов в порах и трещинах породы называется пластовым (поровым) и в данной задаче определяется по формуле: рп = р΄∙рв = р΄ρв∙g∙z=1,06·1000·9,81·3250=33,8 МПа, где р΄ – заданное относительное пластовое давление; рв – давление столба воды на глубине z; ρв – плотность воды ( ρв = 1 г/см3 = 1000 кг/м3). Пластовое давление оказывает существенное влияние на напряжения в скелете горной породы. Учет этого влияния дал следующие формулы: 3в = pп + (pг – рп)/сн = 33,8+(77,47 – 33,8)/0,610 = 105,39 МПа; σ1н = λнрг + рп(1 н)(1 сн) = 0,372·77,47+33,8·(1 – 0,372)∙(1 – 0,610) = 37,1 МПа; сн = ехр(-19,05mв2) = exp(-19,05· 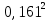 ) = 0,610, ) = 0,610, где σ3в и σ1н – расчетные вертикальные и горизонтальные напряжения в скелете породы; сн – коэффициент, учитывающий влияние пористости на долю сечения, занятую скелетом; mв - верхнее значение пористости в долях единицы. 3. Расчёт предельных давлений в скважине из условия сохранения стенок в упругом состоянии Для осадочных пород предпочтительней теория Мора-Кулона, в соответствии с которой условие упругого состояния стенок скважины τmax < kдл∙τs , где τmax – максимальные касательные напряжения в стенке скважины; kдл – коэффициент длительной прочности; τs – предел текучести горной породы. Поскольку управление напряжениями в стенке скважины осуществляется изменением давления жидкости в скважине, то рsн < рс < psв , где psн и рsв – нижнее и верхнее значения давления в скважине. Отличие касательных напряжений в окрестности скважины от естественных обусловлено неравенствами естественных напряжений и давления бурового раствора в скважине (рс). Заведомо соотношение их величин неизвестно, а поэтому выполняются три расчета: 1) если ztR , то max = (z - R)/2; cр = (z + R)/2; 2) если tzR , то max = (t - R)/2; cр = (t + R)/2; 3) если zRt , то max = (z - t)/2; cр = (z + t)/2, где z , t и R – вертикальная, тангенциальная и радиальная компоненты напряжений, действующих в стенке скважины: z = 3в; R = pп + (ps – рп)/сн; σt = 21н R , где ps – предельное давление жидкости в скважине при max = kдлs, τmax = kдл (Аср +τ0) Первые два случая имеют место, когда давление жидкости в скважине меньше бокового давления горных пород и расчет дает ограничение давления бурового раствора снизу. В третьем случае давление жидкости в скважине больше бокового давления горных пород и расчет дает ограничение давления бурового раствора сверху. Расчетные формулы для определения рs имеют вид: при kдл = 1 в первом случае: ps1 = pп∙(1сн)+[сн3в∙ (1kдл∙Ā)–2kдл∙0]/(1+kдл∙Ā) = 33,8·(1–0,610)+[0,610·105,39∙(1–1·0,444)–2·1·42,36]/(1+1·0,444) = -20,73 МПа; во втором случае: ps2 = pп∙(1сн) + сн∙1н∙(1kдл∙Ā) – kдл∙0 = 33,8·(1–0,610)+ 0,610·37,1·(1–1·0,444)–1·42,36 = -16,59 МПа; в третьем случае: ps3 = pп∙(1сн)+ 2сн∙1н+[2kдл∙0 сн∙3в (1kдл∙Ā)]/(1+kдл∙Ā) = 33,8· (1–0,610)+2·0,610·37,1+[2·1·42,36–0,610·105,39·(1–1·0,444)]/(1+1·0,444) = 92,36 МПа. при kдл = 0,64 ps1 = pп∙(1сн)+[сн3в∙ (1kдл∙Ā)–2kдл∙0]/(1+kдл∙Ā) = 33,8·(1–0,610)+[0,610·105,39∙(1–0,64·0,444)–2·0,64·42,36]/(1+0,64·0,444) = 6,8 МПа; во втором случае: ps2 = pп∙(1сн) + сн∙1н∙(1kдл∙Ā) – kдл∙0 = 33,8·(1–0,610)+ 0,610·37,1·(1–0,64·0,444)–0,64·42,36 = 2,27 МПа; в третьем случае: ps3 = pп∙(1сн)+ 2сн∙1н+[2kдл∙0 сн∙3в (1kдл∙Ā)]/(1+kдл∙Ā) = 33,8· (1–0,610)+2·0,610·37,1+[2·0,64·42,36–0,610·105,39·(1–0,64·0,444)]/(1+0,64·0,444) = 64,83 МПа. Из полученных ps1 и ps2 взяли большее и обозначили его psн . Величина ps3 = psв. Тогда при kдл = 1: pcн = -16,59 МПа, pсв = 92,36 МПа; при kдл = 0,64: pсн = 6,8 МПа, pсв = 64,83 МПа. 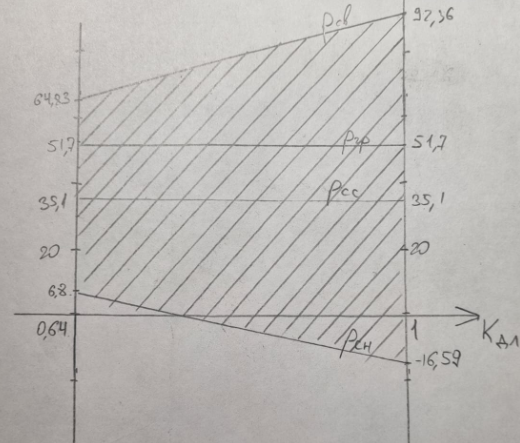 4. Расчёт предельных давлений в скважине из условий предупреждения притока пластовых флюидов и гидроразрыва. При бурении скважины присутствуют две текучие среды: буровой раствор в скважине и пластовый флюид во вскрываемых скважиной горных породах. Для обеспечения нормальных условий бурения каждая из сред должна находиться на своем месте: скважинная жидкость в скважине и циркуляционной системе буровой, а пластовая - в пласте. В соответствии с «Едиными техническими правилами…» для предупреждения притока флюидов в скважину необходимо, чтобы рс > рп, а именно: При глубинах более 2500 м статическое давление в скважине должно быть больше пластового на 4…7 %, но не более, чем на 3,5 МПа. Отсюда рсс = р΄·ρв·g(125 + z)·10-6, МПа = 1,06·1000∙9,81∙(125+3250) = 35,1 МПа Если рсс − рп > 3,5 МПа, то принять рсс = 3,5 + рп, МПа. рсс − рп = 35,1 – 33,8 = 1,3 МПа Результатом расчета является величина рсс, называемая нормальным противодавлением бурового раствора по отношению к пластовым флюидам. В реальных условиях бурения возможны ситуации, когда необходимо бурить при равенстве давления бурового раствора в скважине и пластового давления (бурение на равновесии), и при превышении пластового давления над давлением в скважине (бурение на депрессии). Это специальные виды бурения, которые требуют специального оборудования устья скважины. Гидроразрыв обусловлен возникновением на стенке скважины растягивающих напряжений. ргр =рг + рп(1 ) = 0,4177,47+33,8(1–0,41) = 51,7 МПа. = μср/(1- μср) = 0,29/(1-0,29)=0,41 5. Принятие решения о давлении бурового раствора в скважине и выбор его плотности Выбранная плотность бурового раствора для заданного интервала бурения (пласта) является основным итогом расчетных домашних заданий. pcc = ρ1gz–Δp; ρ1 = (pcc+Δp)/(gz) = (35,1+3,25)/(9,813250) = 1202 кг/м3; ppc = ρ1gz = 1,20210-39,813250 = 38,35 МПа. Расчет напряжений в стенке скважины: z = 3в = 105,39 МПа; R = pп + (ppc – рп)/сн = 33,8+(38,35-33,8)/0,610 = 41,26 МПа; σt = 21н R = 237,1–41,26 = 32,94 МПа, Анализ соотношения напряжений zRt , поэтому max = (z - t)/2 = (105,36–32,94)/2 = 36,21 МПа; cр = (z + t)/2 = (105,36+32,94)/2 = 69,15 МПа. ВЫВОД Для заданного интервала бурения требуется плотность промывочной жидкости 1202 кг/м3. При этом не будет осыпей, обвалов, поглощений и гидроразрыва. Оценка условий бурения проводится по взаимному расположению графиков предельных давлений: осыпей, обвалов стенок скважины не будет, потому что гидростатическое (pс) давление в скважине больше предельного наименьшего (pнм); не будет пластического деформирования (внутрь массива горной породы) стенок скважины, потому что гидростатическое (pс) давление в скважине меньше предельного наибольшего (pнб); возможен гидроразрыв пласта, так как давление гидроразрыва (pГ) меньше предельного наибольшего давления (pнб);  |