вариант ОГЭ по математике. задание. Огэ математика 52
 Скачать 138.91 Kb.
|
|
ОГЭ математика 52 вариант 1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
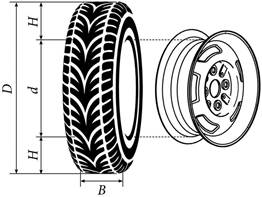
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть  Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13. 2. На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14? 3. На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15? 4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах. 5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых. 6. Найдите значение выражения  7. На координатной прямой отмечены числа  . Какое из следующих утверждений неверно? 1)  2)  3)  4)  8. Найдите значение выражения  при a = 9, b = 36.9. Найдите корни уравнения  Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. 10. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3. 11. Установите соответствие между графиками функций и формулами, которые их задают.  1)  2)  3)  Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах. 13. Решение какого из данных неравенств изображено на рисунке? В ответе укажите номер правильного варианта.  1)  2)  3)  4)  14. Ире надо подписать 880 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Ира подписала 10 открыток. Определите, сколько открыток было подписано за восьмой день, если вся работа была выполнена за 16 дней. 15. 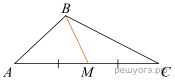 В треугольнике  известно, что  ,  - медиана,  . Найдите  .16.  Сторона  треугольника проходит через центр описанной около него окружности. Найдите  , если  . Ответ дайте в градусах.17.  В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.18.  На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите длину его большей диагонали. 19. Укажите номера верных утверждений. 1) Если при пересечении двух прямых третьей прямой соответственные углы равны 37°, то эти две прямые параллельны. 2) Через любые три точки проходит не более одной прямой. 3) Сумма вертикальных углов равна 180°. Если утверждений несколько, запишите их номера в порядке возрастания. 20. Сократите дробь  21. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе? 22. Постройте график функции  Определите, при каких значениях  прямая  имеет с графиком ровно три общие точки.23. В треугольнике угол  равен 56°, угол  равен 64°,  . Найдите радиус описанной около этого треугольника окружности.24. Окружности с центрами в точках  и  пересекаются в точках  и  , причём точки и лежат по одну сторону от прямой  . Докажите, что прямые  и перпендикулярны.25. Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC. | |||||||||||||||||||||||||||||||||
