лабораторная матлаб. Лабораторная. Оглавление Цель работы 3 Теоретические положения 3 Триангуляция области 5

Название	Оглавление Цель работы 3 Теоретические положения 3 Триангуляция области 5
Анкор	лабораторная матлаб
Дата	06.03.2021
Размер	137.6 Kb.
Формат файла
Имя файла	Лабораторная.docx
Тип	Документы #182340

_{Титульный лист}

Цель работы 3

1.Теоретические положения 3

2.Триангуляция области 5

3.Восстановлении координат тестовой точки по пеленгу 8

4.Расчеты с погрешностями (белый гауссовский шум для пеленгов) 9

Вывод 10

Список использованной литературы 11

Цель работы

Научиться определять местоположение транспортного средства по радиолокационным ориентирам.

Теоретические положения

Классическая задача оценивания векторных параметров по косвенным измерениям предполагает, что результаты измерений (показания приборов) z_i функционально связаны с параметрами ₁,,_m:

z_i_i(₁,,_m, x_i_,1,, x_i_,_l)  e_i,i 1, M, (1)

где _i(₁,,_m, x_i_,1,, x_i_,_l) - некоторые известные скалярные функции; e_i–ошибки измерений;^xi,1 ^,^^,^xi,l– входные переменные, которые измеряются точно или отсутствуют.

Требуется по измерениям найти оценки неизвестных параметров ₁,,_m

Задача в таком виде была сформулирована Гауссом. Для ее решения Гаусс предложил свой знаменитый метод наименьших квадратов (МНК).В настоящее время эта задача формулируется и решается с использованием векторно-матричного подхода.

Зависимости (1) записывают в векторной форме:

Z  (, X)  E

где

Z^T (z₁,, z_M) ,^T(, X)  (₁(, X₁),,_M(, X_M)),^T (₁,,_m) ;

X (X₁,, X_M) ;E^T (e₁,, e_M) . Вектор ошибок E считается распределенным по нормальному закону N_M(0, R_E) .

Требуется по результатам измерений Z, Xнайти оценку ^вектора параметров .

После линеаризации функции (, X) в окрестности некоторой опорной точки ₀ получают МНК-оценку в виде

^^NK ₀ (Q^T R ^¹Q)^¹Q^TR ^¹(Z  (, X)) , (3)

Полученную оценку (3) используем в задаче оценивания декартовых координат объекта на плоскости xoy угломерным способом в многопозиционных локационных системах. Из M базовых точек (позиций) A₁ (x₁, y₁),…,A_M (x_M, y_M) измеряются углы на объект, в результате чего получают значения углов ₁,,_M(рис. 1). Величины ₁,,_M независимы и распределены по нормальному закону N(a_i,) , где a_iточное значение i -го угла, ²–дисперсия ошибок измерений углов. Координаты x_i, y_i базовых точек будем считать известными. По имеющимся измерениям необходимо оценить вектор координат объекта ^T (x_c, y_c) .

Опишем алгоритм расчета МНК-оценки (3). Соотношения (1) в данном случае имеют вид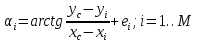

так что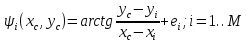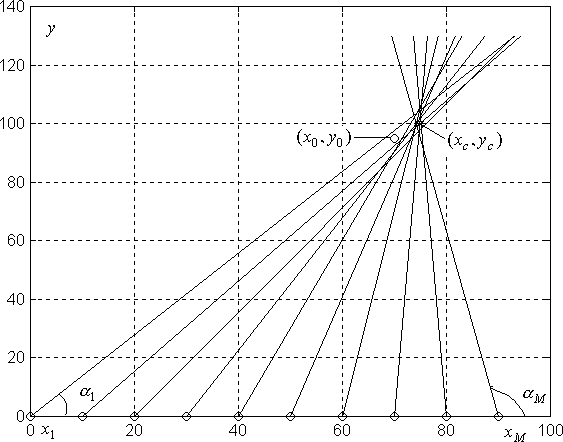

Рисунок 1. Графическая иллюстрация задачи оценивания местоположения объекта по измерениям пеленгов

В векторной форме записи (2) будем иметь следующие обозначения:

Z^T (_i) ,^T(x_c, y_c)  (_i(x_c, y_c)), E^T (e_i) , i  1,M .

Поскольку ошибки измерений e_iнезависимы и имеют одну и ту же дисперсию ², то ковариационная матрица вектора E равна R_E ²I ,где I – единичная (M  M )-матрица. В этом случае оценка (3) приводится к

^^NK ₀ (Q^TQ)^¹Q^T(Z  (₀)),

0
где ^T (x₀, y₀) опорная точка.

Триангуляция области

clear all;

close all;

rand('state',0);

x=[0 0 1 1 rand(1) rand(1)];

y=[0 1 0 1 rand(1) rand(1)];

x=x';

y=y';

TRI = delaunay(x,y);

disp('Матрица инцидентности');

disp(TRI);

trimesh(TRI,x,y,zeros(size(x)));

axis([0 1 0 1]); hold on;

plot(x,y,'o');

x0=rand(1);

y0=rand(1);

Возьмем в локальной системе координат 6 ориентиров. По этим 6 ориентирам построим матрицу инцидентности и определим различные сочетания между ориентирами для построения треугольников.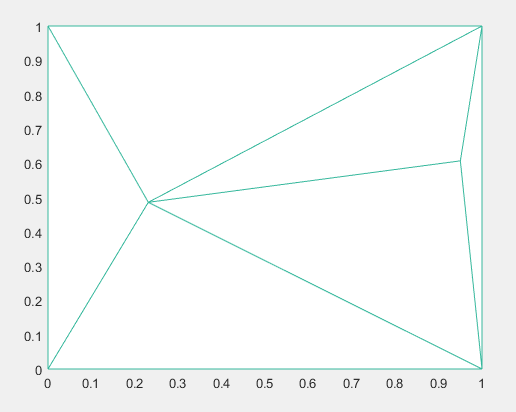

Рисунок 2 – Триангулированная область

Определение тестовой точки и треугольника, в котором она находится

figure();

trimesh(TRI,x,y,zeros(size(x)));

axis([0 1 0 1]); hold on;

plot(x,y,'o');

T=tsearchn([x y],TRI,[x0 y0]);

while isnan(T)

x0=rand(1);

y0=rand(1);

T=tsearchn([x y],TRI,[x0 y0]);

end;

TT=TRI(T,:);

x1=[x(TT(1)); x(TT(2)); x(TT(3))];

y1=[y(TT(1)); y(TT(2)); y(TT(3))];

TRI1 = delaunay(x1,y1);

t=trimesh(TRI1,x1,y1,zeros(size(x1)));

t.FaceColor = 'g';

t.LineStyle = '--';

p=plot(x0,y0,'o');

p.MarkerFaceColor='r';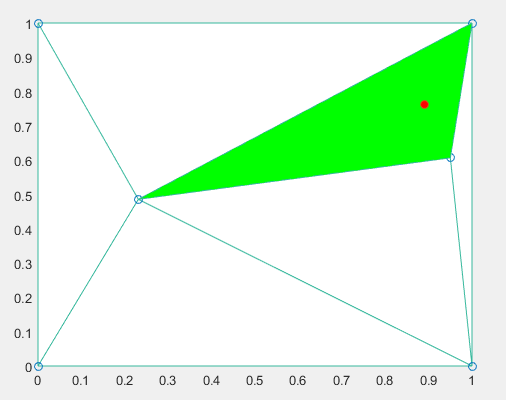

Рисунок 3 – Найденный треугольник

Рассмотренный метод получения местоположения точек однозначно определяет нужный нам картированный треугольник.

figure();

hold on;

x2=[x1; x1(1)];

y2=[y1; y1(1)];

plot(x2,y2);

title('Картированный треугольник');

p=plot(x0,y0,'o');

p.MarkerFaceColor='r';

%Пеленги

T1=[x1(1);y1(1);0];

T2=[x1(2);y1(2);0];

T3=[x1(3);y1(3);0];

X0=[x0 ;y0;0];

a=X0-T1;

b=T2-T1;

Pel(1)= atan2(norm(cross(a,b)),dot(a,b));

a=X0-T2;

b=T1-T2;

Pel(2) = -atan2(norm(cross(a,b)),dot(a,b));

%Восстановление по пеленгу

k0=-(y1(1)-y1(2))./(x1(2)-x1(1));

b0=-(x1(1).*y1(2)-x1(2).*y1(1))./(x1(2)-x1(1));

PP(1)=Pel(1)+atan(k0);

PP(2)=Pel(2)+atan(k0);

Tg=tan(PP);

b1=y1(1)-Tg(1)*x1(1);

b2=y1(2)-Tg(2)*x1(2);

xx=(b2-b1)./(Tg(1)-Tg(2));

yy=(Tg(1).*b2-Tg(2).*b1)./(Tg(1)-Tg(2));

plot(xx,yy,'*g');

hold off;

Восстановлении координат тестовой точки по пеленгу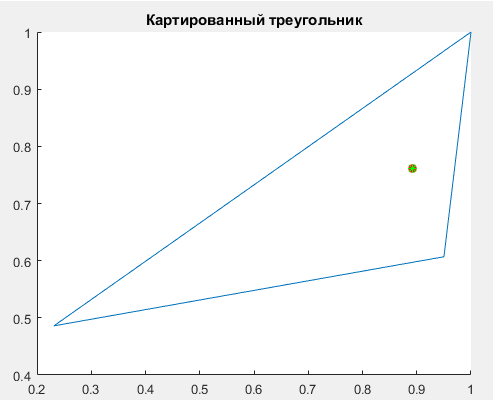

Рисунок 4 – Тестовая и восстановленная точка без погрешности измерения

На рисунке видно, что без введения погрешностей координаты точки восстанавливаются точно.

%Восстановление с белым шумом

figure();

hold on;

plot(x2,y2);

title('Сигма = 0,1');

p=plot(x0,y0,'o');

p.MarkerFaceColor='r';

sigma=0.1;

Pel1=Pel+(randn * sigma);

PP(1)=Pel1(1)+atan(k0);

PP(2)=Pel1(2)+atan(k0);

Tg=tan(PP);

b1=y1(1)-Tg(1)*x1(1);

b2=y1(2)-Tg(2)*x1(2);

xx=(b2-b1)./(Tg(1)-Tg(2));

yy=(Tg(1).*b2-Tg(2).*b1)./(Tg(1)-Tg(2));

plot(xx,yy,'*g');

%Зависимость точности восстановления коордитан от величины sigma

sigma=1;

for i=0:100

Pel1=Pel+(randn * sigma);

for j=1:10

PP(1)=Pel1(1)+atan(k0);

PP(2)=Pel1(2)+atan(k0);

Tg=tan(PP);

b1=y1(1)-Tg(1)*x1(1);

b2=y1(2)-Tg(2)*x1(2);

xx=(b2-b1)./(Tg(1)-Tg(2));

yy=(Tg(1).*b2-Tg(2).*b1)./(Tg(1)-Tg(2));

KK(j+1)=norm([x0 y0]-[xx yy]);

randn;

end;

Porg(i+1,1)=sigma;

Porg(i+1,2)=mean(KK).*100;

sigma=sigma./2;

end;

figure();

hold on;

title('Звисимость погрешности восстановления от Sigma');

plot(Porg(:,1),Porg(:,2),'-');

xlabel('Сигма');

ylabel('Значение погрешности, %');

Расчеты с погрешностями (белый гауссовский шум для пеленгов)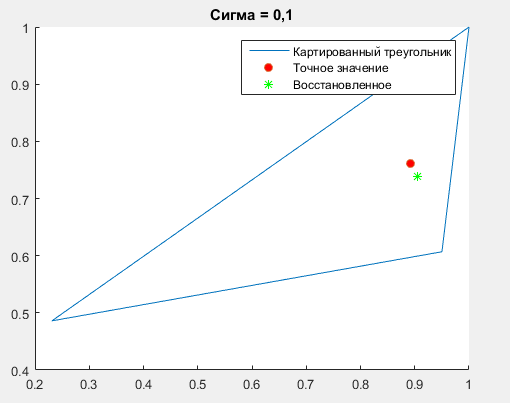

Рисунок 5 – Погрешность измерения Сигма =0,1

При введении погрешности измерения пеленгов явно получаем погрешность определения координат тестовой точки.

Рассмотрим оценку погрешности полученного результата как расстояние от восстановленной точки до тестовой. Проведем эксперименты по опредлению координат точки при изменении дисперсии введенной ошибки.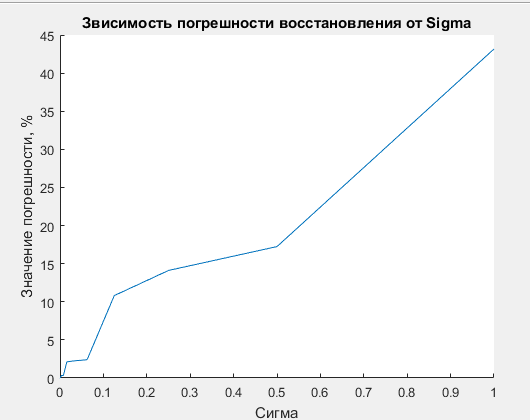

Рисунок 6 – Зависимость точности определения точки от погрешности измерения.

По графику видно, что при увеличении дисперсии введенной ошибки увеличивается погрешность полученного результата.

Вывод

В процессе выполнения работы мы изучили методы получения координат точки по пеленгам в идеальных условиях и в присутствии ошибки измерерния. Полученные результаты экспериментов говорят о том, что точность получения координат точки по пеленгам напрямую зависит от погрешности измерений, в данном случае – от введенной случайной составляющей

Список использованной литературы

Kovacs, P. ECG signal generator based on geometrical features / Р. Kovacs // Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Computatorica. – 2012. – № 37. – P. 247-260.
Jokic, S. Efficient ECG Modeling using Polynomial Functions / S. Jokic, V. Delic, Z. Peric, S.Krco, D. Sakac // Electronics and Electrical Engineering – Kaunas: Technologija. – 2011. – N. 4(110). – P. 121-124.
Вайсман, М. В. Алгоритм синтеза имитационных электрокардиосигналов для испытания цифровых электрокардиографов / М. В. Вайсман, Д. А. Прилуцкий, С. В. Селищев // Электроника. – 2000. – № 4. – С. 21-24.
Белоцерковский, О. М. Способ кодирования данных ЭКГ в модели контурного и динамического анализа ЭКГ / О. М. Белоцерковский, А. В. Виноградов, Э. Э. Галатян, А. С. Тарасов, С. В. Шебко // Компьютер и мозг. Новые технологии. – М.: Наука, 2005. – С. 241-255.
Костенков, С. Ю. Методика формирования математических моделей электрофизиологических сигналов / С. Ю. Костенков // Научно-методический журнал: XXI век: итоги прошлого и проблемы настоящего плюс Периодическое научное издание Серия: «Технические науки. Информационные технологии». – Пенза 03(19). – 2014. – С. 125-132.