Охарактеризуйте гипотезы случайного блуждания: ГСБ-1, ГСБ-2, ГСБ-3. Какие особенности характерны для финансового процесса броуно. Эссе Финансовая эконометрика Васьков. Охарактеризуйте гипотезы случайного блуждания гсб1, гсб2, гсб какие особенности характерны для финансового процесса броуновского движения Что такое арифметическое и геометрическое броуновское движение
 Скачать 38.21 Kb. Скачать 38.21 Kb.
|
|
«Охарактеризуйте гипотезы случайного блуждания: ГСБ-1, ГСБ-2, ГСБ-3. Какие особенности характерны для финансового процесса броуновского движения? Что такое «арифметическое» и «геометрическое» броуновское движение?» Большое число моделей, рассматриваемых в рамках финансовой эконометрики, основывается на предположении о тождественности приростов цен случайному процессу, приросты которого и функциональные преобразования этих приростов имеют свои определенные распределения. Это предположение является так называемой “гипотезой случайного блуждания” (ГСБ). На данный момент существует три версии гипотезы случайного блуждания, различия которых заключаются в особенностях указанных распределений. Первая версия гипотезы случайного блуждания – ГСБ-1 – гласит, что случайные приросты финансового показателя, а также их любые функциональные изменения и преобразования независимы и удовлетворяют условию стационарности (то есть предполагается соблюдение условий постоянства математического ожидания, дисперсии и автокорреляционной функции указанного процесса независимо от временного интервала), или же иначе указанные процессы имеют одинаковые условные распределения на уровни финансовых показателей в рассматриваемые моменты времени. Таким образом, ГСБ-1 утверждает, что динамика приростов цены по своим свойствам соответствует процессу “строгого белого шума”, где все взаимные моменты (кроме центрального и начального) равны нулю. Рассмотрим ГСБ-1 на примере ортогонального условия: Применимо к нему, в рамках ГСБ-1 f(zt) b g(zt-k) могут рассматриваться и как линейные, и как степенные функции от приростов z. Теперь рассмотрим ГСБ-2. Ее отличия от ГСБ-1 обусловлены неодинаково распределенными приращениями, и таким образом, ГСБ-2 уже не является стационарным процессом. Смягчающее обстоятельство обусловливается тем, что по результатам анализа динамики многих финансовых показателей на мировых рынках было отмечено, что при сохранении вида самого закона параметры распределение приростов изменяются, и чаще всего такое происходит с дисперсией. Дальнейшие послабления условия полной независимости процесса приращений цен приводит к третьей версии ГСБ – ГСБ-3, согласно которой автокорреляционные связи между приростами отсутствуют, однако автокорреляция между их степенями может иметь место. Стандартное одномерное броуновское движение – это непрерывный стохастический процесс z={zt}, определенный на вероятностном пространстве (Ω, F, P), такой что: - Значение в начальный момент времени zt0 = 0 почти всюду; - zti+1−zti ∼ N(0,ti+1−ti). Приращение zti+1−zti имеет нормальное распределение с математическим ожиданием, равным нулю, и дисперсией равной ti+1 – ti; ∀i = 0,...,n − 1; Для любых промежутков времени 0 = t0 < t1 < t2 < ... < tn приращения zt1 − zt0 , zt2 − zt1 ,..., ztn−1 − ztn независимы ∀i = 0,...,n − 1. Стандартное броуновское движение характеризуется следующими особенностями: — это процесс с непрерывным временем. — это случайный процесс, в котором наилучшим предсказанием поведения процесса в будущем является его настоящее состояние. Величина дисперсии за время h есть V ar(zt+h − zt)2 = h. Арифметическое броуновское движение x˜ = {x˜t}t≥0 можно определить с помощью стандартного броуновского движения, описанного выше. Его характеризует ненулевое начальное значение и ожидаемое значение тренда. 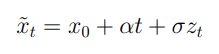 Арифметическое броуновское движение можно представлять себе как аккумуляцию независимых, стационарных и нормально распределенных приращений dx в течение множества непересекающихся малых интервалов времени длины dt, с приращениями, имеющими математическое ожидание αdt и дисперсию σ2dt. 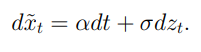 Геометрическое броуновское движение - случайный процесс с непрерывным временем, являющийся экспоненциальной формой броуновского движения. Широко используется для моделирования изменений цен на актив во времени, так как может принимать только положительные значения, что является хорошей аппроксимацией поведения цен, который, однако не учитывает редкие события (выбросы). 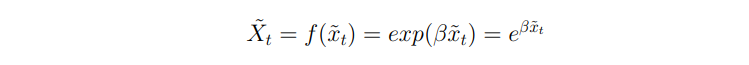 |
