Задачи. Финальная версия задач. Омский колледж библиотечноинформационных технологий
 Скачать 21.69 Kb.
|
|
Бюджетное профессиональное образовательное учреждение Омской области "Омский колледж библиотечно-информационных технологий" ДОМАШНЕЕ ЗАДАНИЕ
Омск 2021 Теория вероятности Задача 1 На конкурсе выступают 11 участников из Казани, 6 участников из Нижнего Новгорода, 3 участника из Москвы и 7 участников из Твери. Порядок выступления в конкурсе определяется жеребьевкой. Какова вероятность того, что последним будем выступать конкурсант из Нижнего Новгорода? Результат округлите до сотых. Решение. Итак, представим, что все конкурсанты подошли к барабану, где лежат номерки и тянут по одному номерку. Общее количество конкурсантов n = 11 + 6 + 3 + 7 = 27. Нас интересует, какова вероятность того, что один из конкурсантов из Нижнего Новгорода вытянет номерок с цифрой 27. Конкурсантов из Нижнего Новгорода всего 6, следовательно m = 6. Таким образом, вероятность будет равна: 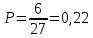 Ответ: 0,22. Задача 2 В соревнованиях по борьбе участвуют 73 участника. Из них 25 участников из Москвы, в том числе Б. Егоров. На пары участники разбиваются с помощью жеребьевки. Какова вероятность того, что противником Б. Егорова станет участник из Москвы? Результат округлите до сотых. Решение. В этой задаче есть фиксированный элемент – Б. Егоров. Это фиксированный элемент мы должны вычесть из элементов m и n. Итак, общее количество участников – 73. Но Б. Егоров у нас уже выбран, поэтому он не участвует в жеребьевке. Следовательно, его мы исключаем из общего количества и получаем n = 72. Нас интересуют только участники из Москвы, их 25. Но опять же Б. Егоров у нас уже выбран, поэтому он не участвует в жеребьевке. Следовательно, количество устраивающих нас вариантов m = 24. Тогда: 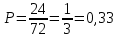 Ответ: 0,33. Задача 3 Стрелок стреляет 6 раз по мишеням. Вероятность попадания стрелка в мишень при каждом выстреле равна 0,8. Какова вероятность того, что стрелок попадет в мишень все 6 раз подряд? Результат округлите до сотых. Решение. В задаче происходит 6 независимых событий – 6 выстрелов. Вероятность каждого из них – 0,8. Чтобы найти вероятность возникновения этих независимых событий одновременно необходимо перемножить вероятности этих событий. Таким образом: 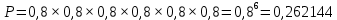 Ответ: 0,26. Задача 4 Стрелок стреляет 6 раз по мишеням. Вероятность попадания стрелка в мишень при каждом выстреле равна 0,8. Какова вероятность того, что стрелок первые 2 раза промахнется, а остальные 4 раза попадет в цель? Результат округлите до сотых. Решение. В задаче происходит 6 независимых событий – 6 выстрелов. Вероятность того, что стрелок попадет или не попадет в мишень, равна 1. Вероятность того, что стрелок попадет в мишень, равна 0,8. Тогда вероятность того, что не попадет в мишень, равна 1 — 0,8 = 0,2. Нам нужно найти вероятность, когда стрелок два раза промахнется, а потом четыре раза попадет. Перемножаем соответствующие вероятности: 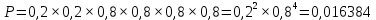 Ответ: 0,02. Задача 5 В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать? Решение: старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т. е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно: 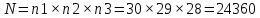 Ответ: 24360. Комбинаторика Задача 1 Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей? Решение: различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить 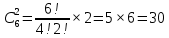 ( 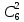способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот). Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше з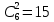наменателя):  способами выбираем два числа из 6, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя.Ответ:30,15. Задача 2 Из 15 школьников нужно отправить 2 учеников на дежурство. Сколькими способами можно это сделать? Решение: 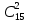 = 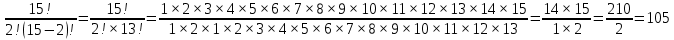Ответ: 105 способов. Задача 3 Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду? Решение: т.к. известно, что двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям). Следовательно, выборки – сочетания из n различных элементов по m элементов, их число: 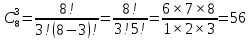 Ответ: 56. Задача 4 Сколько слов можно получить, переставляя буквы в слове Гора и Институт? Решение: В слове «гора» четыре буквы, все они различны, поэтому можно получить всего 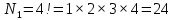 различных слова.В слове «институт» 8 букв, из них две буквы «и», три буквы «т» и по одной букве «н», «с» и «у». Поэтому всего можно получить перестановками бук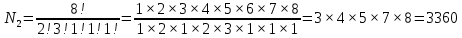в  различных слов.Ответ: 24 и 3360 слов. Задача 5 В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах? Решение: т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n=9, m=4. Число таких размещений находим по формуле: 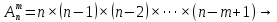 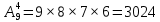 Ответ: 3024 способа рассадить 4 человека. | ||||||||||||||||||||||||||||||||