Эмм Ш. Задачи по теории вероятностей с решениями Комбинаторика

• Название: Задачи по теории вероятностей с решениями Комбинаторика
• Анкор: Эмм Ш
• Дата: 13.11.2021
• Размер: 0.65 Mb.
• Имя файла: Zadaniya_s_rech_kMod1(18.02.13).doc
• Тип: Задача; #271277
• страница: 1 из 3

Задачи по теории вероятностей с решениями
1. Комбинаторика
Задача 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n₁=30, n₂=29, n₃=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно N=n₁n₂n₃=302928=24360.

Задача 2. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?

Решение. Первое письмо имеет n₁=2 альтернативы – либо его относит к адресату первый почтальон, либо второй. Для второго письма также есть n₂=2 альтернативы и т.д., т.е. n₁=n₂=…=n₁₀=2. Следовательно, в силу правила умножения общее число способов распределений писем между двумя почтальонами равно

.

Задача 3. В ящике 100 деталей, из них 30 – деталей 1-го сорта, 50 – 2-го, остальные – 3-го. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?

Решение. Деталь 1-го сорта может быть извлечена n₁=30 способами, 2-го сорта – n₂=50 способами. По правилу суммы существует N=n₁+n₂=30+50=80 способов извлечения одной детали 1-го или 2-го сорта.

Задача 5. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение. Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число равно



Задача 6. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по всем номинациям установлены различные премии?

Решение. Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций, как составом, так и их порядком. Так как каждый фильм может получить призы как по одной, так и по нескольким номинациям, то одни и те же фильмы могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 10 элементов по 5:

Задача 7. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно

Задача 8. В условиях задачи 6 определить, сколько существует вариантов распределения призов, если по всем номинациям установлены одинаковые призы?

Решение. Если по каждой номинации установлены одинаковые призы, то порядок фильмов в комбинации 5 призов значения не имеет, и число вариантов представляет собой число сочетаний с повторениями из 10 элементов по 5, определяемое по формуле



Задача 9. Садовник должен в течении трех дней посадить 6 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?

Решение. Предположим, что садовник сажает деревья в ряд, и может принимать различные решения относительно того, после какого по счету дерева остановиться в первый день и после какого – во второй. Таким образом, можно представить себе, что деревья разделены двумя перегородками, каждая из которых может стоять на одном из 5 мест (между деревьями). Перегородки должны стоять там по одной, поскольку иначе в какой-то день не будет посажено ни одного дерева. Таким образом, надо выбрать 2 элемента из 5 (без повторений). Следовательно, число способов .

Задача 10. Сколько существует четырехзначных чисел (возможно, начинающихся с нуля), сумма цифр которых равна 5?

Решение. Представим число 5 в виде суммы последовательных единиц, разделенных на группы перегородками (каждая группа в сумме образует очередную цифру числа). Понятно, что таких перегородок понадобится 3. Мест для перегородок имеется 6 (до всех единиц, между ними и после). Каждое место может занимать одна или несколько перегородок (в последнем случае между ними нет единиц, и соответствующая сумма равна нулю). Рассмотрим эти места в качестве элементов множества. Таким образом, надо выбрать 3 элемента из 6 (с повторениями). Следовательно, искомое количество чисел

Задача 11. Сколькими способами можно разбить группу из 25 студентов на три подгруппы А, В и С по 6, 9 и 10 человек соответственно?

Решение. Здесь n=25, k=3, n₁=6, n₂=9, n₃=10. Согласно формуле, число таких разбиений равно

Задача 12. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?

Решение. Каждое семизначное число отличается от другого порядком следования цифр, при этом фактически все семь мест в этом числе делятся на три группы: на одни места ставится цифра «4», на другие места – цифра «5», а на третьи места – цифра «6». Таким образом, множество состоит из 7 элементов (n=7), причем n₁=3, n₂=2, n₃=2, и, следовательно, количество таких чисел равно


2. Классическая вероятностная модель. Геометрическая вероятность
Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?

Решение. Элементарными исходами здесь являются наборы, включающие 3 фрукта. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний . Число благоприятствующих исходов равно числу способов выбора 3 апельсинов из имеющихся 5, т.е. . Тогда искомая вероятность

.

Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут.

Решение. Вначале подсчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел и имеет n₁=10 возможностей, второй тоже имеет n₂=10 возможностей, наконец, третий также имеет n₃=10 возможностей. В силу правила умножения общее число способов равно: n= n₁n₂n₃=10³ = 1000, т.е. все пространство содержит 1000 элементарных исходов. Для вычисления вероятности события A удобно перейти к противоположному событию, т.е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет m₁=10 способов выбора числа. Второй студент имеет теперь лишь m₂=9 возможностей, поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента. Третий студент еще более ограничен в выборе — у него всего m₃=8 возможностей. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно m=1098=720. Случаев, в которых есть совпадения, остается 280. Следовательно, искомая вероятность равна Р=280/1000= 0,28.

Задача 3. Найти вероятность того, что в 8-значном числе ровно 4 цифры совпадают, а остальные различны.

Решение. Событие А={восьмизначное число содержит 4 одинаковые цифры}. Из условия задачи следует, что в числе пять различных цифр, одна из них повторяется. Число способов её выбора равно числу способов выбора одной цифры из 10 цифр. Эта цифра занимает любые 4 места в числе, что возможно сделать способами, так как порядок здесь не важен. Оставшиеся 4 места занимают различные цифры из неиспользованных девяти, и так как число зависит от порядка расположения цифр, то число способов выбора четырех цифр равно числу размещений . Тогда число благоприятствующих исходов . Всего же способов составления 8-значных чисел равно ||=10⁸. Искомая вероятность равна

.

Задача 4. Шесть клиентов случайным образом обращаются в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратится.

Решение. Рассмотрим противоположное событие , состоящее в том, что в каждую из 5 фирм обратился клиент, тогда в какую-то из них обратились 2 клиента, а в остальные 4 фирмы – по одному клиенту. Таких возможностей . Общее количество способов распределить 6 клиентов по 5 фирмам . Отсюда . Следовательно, .

Задача 5. Пусть в урне имеется N шаров, из них М белых и N–M черных. Из урны извлекается n шаров. Найти вероятность того, что среди них окажется ровно m белых шаров.

Решение. Так как порядок элементов здесь несущественен, то число всех возможных наборов объема n из N элементов равно числу сочетаний . Число испытаний, которые благоприятcтвуют событию А – "m белых шаров, n–m черных", равно , и, следовательно, искомая вероятность равна Р(А)= .

Задача 6. Точку наудачу бросили на отрезок [0; 2]. Какова вероятность ее попадания в отрезок [0,5; 1,4]?

Решение. Здесь пространство элементарных исходов весь отрезок , а множество благоприятствующих исходов , при этом длины этих отрезков равны и соответственно. Поэтому

.

Задача 7 (задача о встрече). Два лица А и В условились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них может произойти наудачу в течении указанного часа и моменты прихода независимы?

Решение. Обозначим момент прихода лица А через х и лица В – через у. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы ôх-уô£20. Изобразим х и у как координаты на плоскости, в качестве единицы масштаба выберем минуту. Всевозможные исходы представляются точками квадрата со стороной 60, а благоприятствующие встрече располагаются в заштрихованной области. Искомая вероятность равна отношению площади заштрихованной фигуры (рис. 2.1) к площади всего квадрата: P(A) = (60²–40²)/60² = 5/9.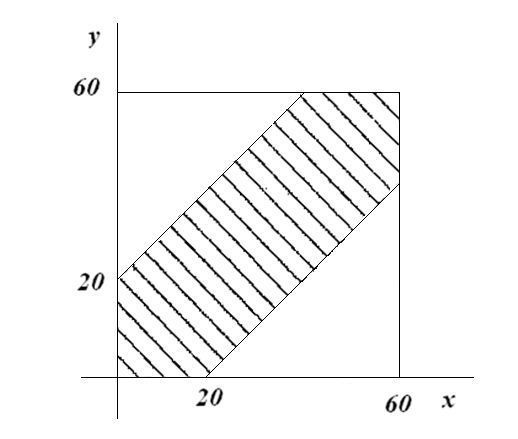



Рис. 2.1.
3. Основные формулы теории вероятностей
Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?

Решение. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы , где события и означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна , а вероятность вытащить две синие пуговицы 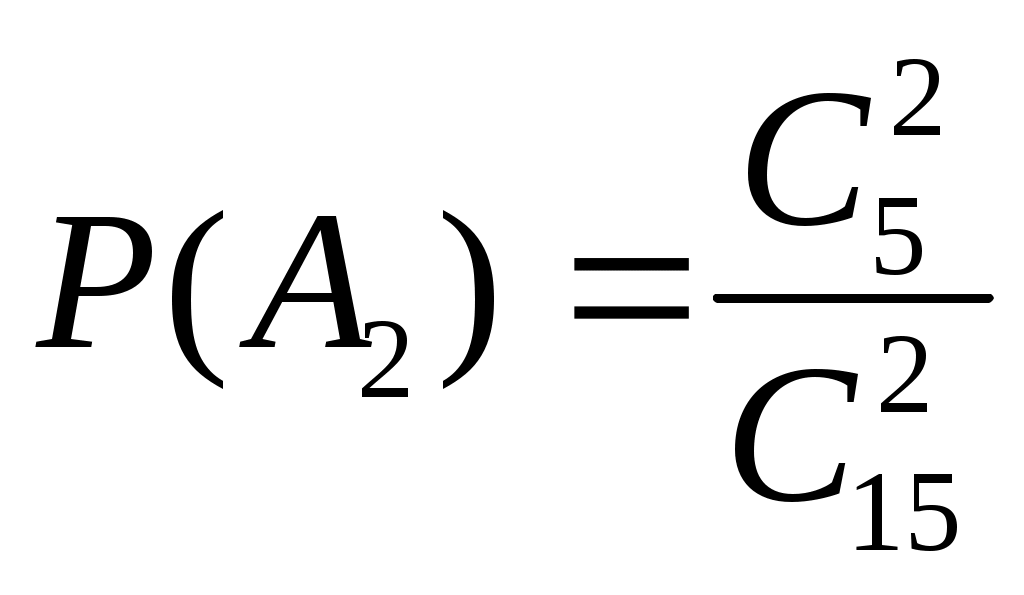. Так как события и не могут произойти одновременно, то в силу теоремы сложения



Задача 2. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.

Решение. Обозначим через A, B и С события, заключающиеся в том, что случайно выбранный сотрудник фирмы владеет английским, немецким или французским соответственно. Очевидно, доли сотрудников фирмы, владеющих теми или иными языками, определяют вероятности этих событий. Получаем:

а) P(AB)=P(A)+P(B) P(AB)=0,28+0,30,08=0,5;

б) P(ABC)=P(A)+P(B)+P(C)(P(AB)+P(AC)+P(BC))+P(ABC)=0,28+0,3+0,42

(0,08+0,1+0,05)+0,03=0,8;

в) 1P(ABC)=0,2.

Задача 3. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?

Решение. Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождение мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола. Старший ребенок – мальчик, следовательно, второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и



Задача 4. Мастер, имея 10 деталей, из которых 3 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?

Решение. Событие А={мастер проверил ровно две детали} означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит, , где ={ первая деталь оказалась нестандартной } и ={вторая деталь – стандартная}. Очевидно, что вероятность события А₁ равна кроме того, , так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных. По теореме умножения



Задача 5. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.

Решение. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы , где события и означают появление белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна , а вероятность вытащить белый шар из второго ящика . Кроме того, в силу независимости и имеем: . По теореме сложения получаем: .

Задача 6. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим через гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

, , .

Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи

, , .

По формуле полной вероятности получаем:

.

Задача 7. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?

Решение. Пусть событие G – появление годной детали. Вероятности гипотез о том, что деталь поставлена фирмами А, B, С, равны сответственно Р(А)=0,5, Р(В)=0,3, Р(С)=0,2. Условные вероятности появления при этом годной детали равны Р(G|A)=0,9, P(G|B)=0,95, P(G|C)=0,94 (как вероятности противоположных событий к появлению бракованной). По формуле полной вероятности получаем:

P(G)=0,50,9+0,30,95+0,20,94=0,923.

Задача 8 (см. задачу 6). Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?

Решение. Вероятность получить «неуд» равна . Требуется вычислить условные вероятности. По формулам Байеса получаем:

, и аналогично,

, .

Отсюда следует, что, вероятнее всего, слабо подготовившийся студент сдавал экзамен третьему экзаменатору.