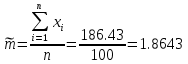Вариант 13
В урне один белый и пять черных шаров. Два игрока по очереди вынимают из урны шар и возвращают его обратно, после чего шары в урне перемешиваются. Выигрывает тот, кто первый извлекает белый шар. Какова вероятность того, что выиграет игрок, начинающий игру?
Решение
Вероятность появления белого шара равна
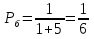
Вероятность появления черного шара равна

Для первого игрока возможны следующие исходы
Вынут белый шар 
Первый игрок вынул черный шар, второй игрок вынул черный шар, первый игрок вынул белый шар
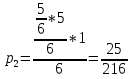
Первый игрок вынул черный шар, второй игрок вынул черный шар, первый игрок вынул черный шар, второй игрок вынул черный шар, первый игрок вынул белый шар
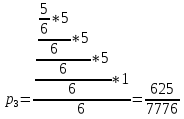
Искомая вероятность
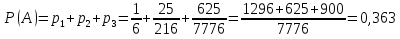
Ответ: Р(А)=0,363
По каналу связи, подверженному воздействию помех, передается одна из двух команд управления в виде кодовых комбинации 11111 или 00000, причем априорные вероятности передачи этих команд соответственно равны 0,7 и 0,3. Из-за наличия помех вероятность правильного приема каждого из символов (1 и 0) уменьшается до 0,6. Предполагается, что символы кодовых комбинаций искажаются независимо друг от друга. На входе приемного устройства зарегистрирована комбинация 10110. Определить, какая команда была передана?
Решение
Пусть А - событие, состоящее в приеме комбинации 10110. К этому событию ведут две гипотезы: Н1 - была передана комбинация 11111; Н2 - была передана комбинация 00000. По условию  ; ;  . Условная вероятность приема кодовой комбинации 10110 вместо 11111 равна . Условная вероятность приема кодовой комбинации 10110 вместо 11111 равна
 ; условная вероятность приема 10110 вместо 00000 равна ; условная вероятность приема 10110 вместо 00000 равна  . .
По формуле гипотез находим


На основании сравнения найденных условных вероятностей заключаем, что при появлении на выходе комбинации 10110 с вероятностью 0,78 была передана команда 11111.
На окружность радиуса R брошено две точки. Считая, что длина хорды – случайная величина с равномерным распределением, найти плотность распределения вероятностей дуги между брошенными точками.
Решение



Каждая повторная передача сигнала по каналу связи увеличивает вероятность искажения сигнала на 0,1%. При передаче первого сигнала эта вероятность равна 0,05. Передано 100 сигналов. Найти границы, в которых с вероятность 0,9 заключено число переданных без искажения сигналов.
Решение
Вероятность того, что будет искажен 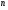 -й сигнал -й сигнал
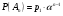 , ,
где  . .
Вероятность искажения последнего сигнала
 , ,
Поскольку вероятности  отличаются незначительно, будем приближенно считать случайную величину отличаются незначительно, будем приближенно считать случайную величину  - количество исказившихся сигналов – распределенной по биномиальному закону. Так как з=0,001 , а значение - количество исказившихся сигналов – распределенной по биномиальному закону. Так как з=0,001 , а значение 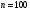 достаточно велико, можно считать случайную величину достаточно велико, можно считать случайную величину  распределенной нормально с математическим ожиданием распределенной нормально с математическим ожиданием 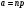 и средним квадратическим отклонением и средним квадратическим отклонением  : :
 , ,
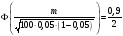 , ,
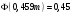 , ,
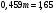 , ,
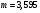 . .
Таким образом, количество искаженных сигналов из числа всех переданных с доверительной вероятностью  лежит в интервале лежит в интервале
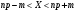 , ,
 , ,
 . .
Число 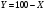 сигналов, переданных без искажений, будет, таким образом, заключено в интервале сигналов, переданных без искажений, будет, таким образом, заключено в интервале 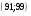 . .
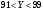 . .
Случайная величина (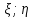 ) распределена по нормальному закону с математическим ожиданием ) распределена по нормальному закону с математическим ожиданием 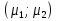 и ковариационной матрицей и ковариационной матрицей
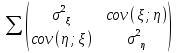
Найти 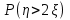  
Решение
P{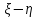 > 0} > 0}
Рассмотрим  ; ; 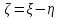


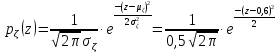

P{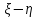 > 0} = > 0} =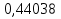
Для заданной выборки:
постройте: а) статистический ряд; б)интервальный статистический ряд, предварительно определив число интервалов;
найдите значения точечных оценок математического ожидания и дисперсии
постройте гистограмму
на основе анализа результатов наблюдений выдвинете гипотезу о виде закона распределения генеральной совокупности
1,8
|
1,4
|
1,12
|
2,3
|
2,7
|
3,3
|
1,3
|
1,13
|
1,7
|
1,4
|
1,25
|
1,9
|
1,64
|
1,47
|
1,65
|
1,5
|
1,85
|
1,68
|
1,51
|
1,48
|
1,95
|
0,8
|
2,8
|
2,4
|
2,95
|
2,5
|
2,3
|
2,9
|
1,84
|
2,2
|
1,68
|
2,5
|
2,52
|
1,29
|
3,3
|
1,85
|
2,1
|
3,6
|
2,4
|
2,55
|
1,5
|
1,29
|
1,85
|
1,58
|
1,31
|
1,69
|
1,28
|
1,9
|
1,87
|
1,7
|
1,49
|
2,1
|
1,9
|
1,49
|
1,8
|
2,45
|
2,3
|
3,0
|
3,1
|
3,1
|
1,6
|
1,88
|
2,2
|
1,63
|
0,8
|
1,63
|
1,45
|
1,29
|
1,47
|
2,55
|
1,49
|
2,4
|
2,55
|
1,26
|
0,8
|
1,25
|
2,1
|
0,7
|
2
|
1,85
|
0,9
|
1,9
|
2,1
|
2,55
|
2,55
|
2,4
|
0,6
|
2,1
|
0,4
|
2,5
|
1,5
|
1,69
|
2,7
|
1,48
|
1,5
|
1,69
|
1,46
|
1,48
|
1,52
|
1,3
|
Решение
а) статистический ряд
0,4
|
0,6
|
0,7
|
0,8
|
0,9
|
1,12
|
1,13
|
1,25
|
1,26
|
1,28
|
1,29
|
1,3
|
1,31
|
1,4
|
1,45
|
1,46
|
1,47
|
1,48
|
1,49
|
1,5
|
1
|
1
|
1
|
3
|
1
|
1
|
1
|
2
|
1
|
1
|
3
|
2
|
1
|
2
|
1
|
1
|
2
|
3
|
3
|
4
|
1,51
|
1,52
|
1,58
|
1,6
|
1,63
|
1,64
|
1,65
|
1,68
|
1,69
|
1,7
|
1,8
|
1,84
|
1,85
|
1,87
|
1,88
|
1,9
|
1,95
|
2
|
2,1
|
2,2
|
1
|
1
|
1
|
1
|
2
|
1
|
1
|
2
|
3
|
2
|
2
|
1
|
4
|
1
|
1
|
4
|
1
|
1
|
5
|
2
|
2,3
|
2,4
|
2,45
|
2,5
|
2,52
|
2,55
|
2,7
|
2,8
|
2,9
|
2,95
|
3
|
3,1
|
3,3
|
3,6
|
3
|
4
|
1
|
3
|
1
|
5
|
2
|
1
|
1
|
1
|
1
|
2
|
2
|
1
|
интервальный статистический ряд - 9 интервалов
[0;0,4)
|
[0,4;0,8)
|
[0,8;1,2)
|
[1,2;1,6)
|
[1,6;2,0)
|
[2,0;2,4)
|
[2,4;2,8)
|
[2,8;3,2)
|
[3,2;3,6]
|
1
|
2
|
6
|
29
|
26
|
11
|
16
|
6
|
3
|
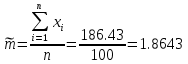

Гистограмма
Полигон
Нельзя однозначно сказать о законе распределения, но можно выдвинуть гипотезу о нормальном распределении совокупности.
Для исследования стабильности температуры в термостате, в который помещается кварцевый генератор с интервалом в 15 часов проведены две серии замеров температуры t0C
серия
|
Замер
|
1
|
2
|
3
|
4
|
5
|
6
|
1-я
|
17,85
|
17,98
|
18,01
|
18,2
|
17,9
|
18,0
|
2-я
|
18,01
|
17,98
|
18,05
|
17,9
|
18,0
|
-
|
Проверить гипотезу о неизменности температуры в термостате, если точность измерения температуры характеризуется средним квадратичным отклонением  , случайные ошибки измерения подчинены нормальному закону распределения, а уровень значимости , случайные ошибки измерения подчинены нормальному закону распределения, а уровень значимости 
Решение
Определим среднее значение и дисперсию для каждой серии испытаний


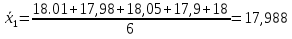
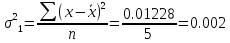
Проверим гипотезу  (о равенстве дисперсий) при альтернативной гипотезе (о равенстве дисперсий) при альтернативной гипотезе  . .

распределение Фишера со степенями свободы  и и  . .
По таблице квантилей распределения Фишера находим  . .
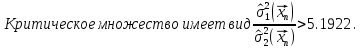

Гипотезу 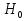 отвергаем , т.к. отвергаем , т.к. 
Известно, что измерительный прибор не имеет систематических ошибок, а случайные ошибки каждого измерения подчиняются одному и тому же нормальному закону распределения. Сколько надо провести измерений для определения оценки измерений величины, чтобы с доверительной вероятностью 0,7 абсолютное значение ошибки в определении этой величины было не более 20%?
Решение
Результаты каждого измерения – независимые нормально распределенные случайные величины. Пусть математическое ожидание каждой из них равно  , а среднее квадратическое отклонение , а среднее квадратическое отклонение 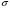 . Тогда среднее арифметическое этих величин . Тогда среднее арифметическое этих величин  – нормально распределенная случайная величина с математическим ожиданием – нормально распределенная случайная величина с математическим ожиданием  и средним квадратическим отклонением и средним квадратическим отклонением 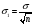 . Вероятность того, что она отклонится от своего математического ожидания не более, чем на . Вероятность того, что она отклонится от своего математического ожидания не более, чем на 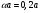
 . .
Предполагая, что  (в противном случае погрешности будут сопоставимы с результатами измерений), получим: (в противном случае погрешности будут сопоставимы с результатами измерений), получим:
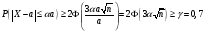 , ,
 , ,
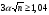 , ,
 , ,
 . .
Таким образом, достаточно трех измерений, чтобы с доверительной вероятностью 0,7 абсолютное значение ошибки в определении величины не превышало 20%.
Т.о, 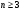 |
 Скачать 99.28 Kb.
Скачать 99.28 Kb.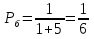

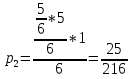
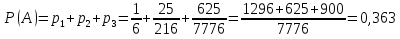





 -й сигнал
-й сигнал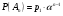 ,
, .
. ,
, отличаются незначительно, будем приближенно считать случайную величину
отличаются незначительно, будем приближенно считать случайную величину  - количество исказившихся сигналов – распределенной по биномиальному закону. Так как з=0,001 , а значение
- количество исказившихся сигналов – распределенной по биномиальному закону. Так как з=0,001 , а значение  достаточно велико, можно считать случайную величину
достаточно велико, можно считать случайную величину  распределенной нормально с математическим ожиданием
распределенной нормально с математическим ожиданием 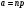 и средним квадратическим отклонением
и средним квадратическим отклонением  :
: ,
,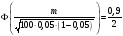 ,
,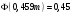 ,
,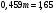 ,
,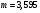 .
. лежит в интервале
лежит в интервале 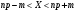 ,
, ,
, .
.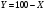 сигналов, переданных без искажений, будет, таким образом, заключено в интервале
сигналов, переданных без искажений, будет, таким образом, заключено в интервале 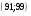 .
.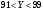 .
.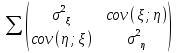
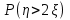


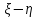 > 0}
> 0} ;
; 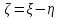


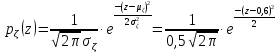

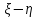 > 0} =
> 0} =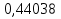

 , случайные ошибки измерения подчинены нормальному закону распределения, а уровень значимости
, случайные ошибки измерения подчинены нормальному закону распределения, а уровень значимости 


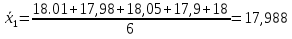
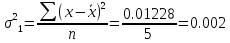
 (о равенстве дисперсий) при альтернативной гипотезе
(о равенстве дисперсий) при альтернативной гипотезе  .
.
 и
и  .
.  .
. 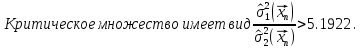

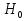 отвергаем , т.к.
отвергаем , т.к. 
 , а среднее квадратическое отклонение
, а среднее квадратическое отклонение 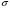 . Тогда среднее арифметическое этих величин
. Тогда среднее арифметическое этих величин  – нормально распределенная случайная величина с математическим ожиданием
– нормально распределенная случайная величина с математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением 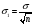 . Вероятность того, что она отклонится от своего математического ожидания не более, чем на
. Вероятность того, что она отклонится от своего математического ожидания не более, чем на 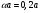
 .
. (в противном случае погрешности будут сопоставимы с результатами измерений), получим:
(в противном случае погрешности будут сопоставимы с результатами измерений), получим: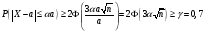 ,
, ,
,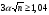 ,
, ,
, .
.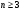


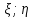 ) распределена по нормальному закону с математическим ожиданием
) распределена по нормальному закону с математическим ожиданием 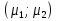 и ковариационной матрицей
и ковариационной матрицей