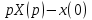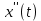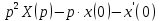Шамиль Раимов. Операционный метод интегрирования линейных дифференциальных уравнений и линейных систем дифференциальных уравнений
 Скачать 131.52 Kb. Скачать 131.52 Kb.
|
|
Курсовая работа на тему «Операционный метод интегрирования линейных дифференциальных уравнений и линейных систем дифференциальных уравнений.» 2023 Содержание Введение……………………………………………………………………………...3 Глава 1. Теоретические аспекты курсовой работы………………………………..5 Операционное исчисление. Функции оригинал..…………………………...5 Преобразование Лапласа. Теоремы преобразования Лапласа……………..6 Решение линейных систем обыкновенных дифференциальных уравнений…………………………………………………………………….11 Глава 2. Эмпирические аспекты курсовой работы……………………………….14 2.1. Пример №1 решения линейных систем обыкновенных дифференциальных уравнений……………………………………………………14 2.2. Пример №2 решения линейных систем обыкновенных дифференциальных уравнений……………………………………………………21 Заключение………………………………………………………………………….24 Список использованных источников……………………………………………...25 Введение Актуальность исследования заключается в том, что операционное исчисление в настоящее время стало одной из важнейших глав практического математического анализа. Операционный метод непосредственно используется при решении обыкновенных дифференциальных уравнений и систем таких уравнений; его можно использовать и при решении дифференциальных уравнений в частных производных. Операционное исчисление обратило на себя внимание после того, как английский инженер-электрик Хевисайд, используя символическое исчисление, получил ряд важных результатов. Но недоверие к символическому исчислению сохранялось до тех пор, пока Джорджи, Бромвич, Карсон, А. М. Эфрос, А. И. Лурье, В. А. Диткин и другие не установили связи операционного исчисления с интегральными преобразованиями. Идея решения дифференциального уравнения операционным методом состоит в том, что от дифференциального уравнения относительно искомой функции-оригинала f ( t ) переходят к уравнению относительно другой функции F ( p ), называемой изображением f ( t ) . Полученное операционное уравнение обычно уже алгебраическое (значит более простое по сравнению с исходным). Решая его относительно изображения F ( p ) и переходя затем к соответствующему оригиналу, находят искомое решение данного дифференциального уравнения. Все вышеизложенное указывает на актуальность выбранной нами темы – «Операционное исчисление. Преобразование Лапласа. Решение линейных систем обыкновенных дифференциальных уравнений, примеры.» Проблемой нашего исследования является то, что операционное исчисление- одна из важных тем математического анализа, она в трудах ученых не получила должного математического обоснования. Целью нашего исследования является: изучение особенностей операционного метода и преобразований Лапласа при решении линейных систем обыкновенных дифференциальных уравнений. Объект исследования: математический анализ. Предмет исследования: решение линейных систем обыкновенных дифференциальных уравнений использую операционный метод и преобразования Лапласа. В соответствии с целью, объектом и предметом исследования были поставлены следующие задачи: Изучить состояние операционных исчислений. Выявить основные преобразования Лапласа. Определить теоретические основы операционных исчислений, преобразований Лапласа. Привести примеры решений линейных систем обыкновенных дифференциальных уравнений. Глава 1. Теоретическое обоснование курсовой работы Операционные исчисления. Функции оригинал Операционное исчисление- один из наиболее экономичных методов интегрирования линейных дифференциальных уравнений с постоянными коэффициентами и пользуется большой популярностью у инженеров. Метод был предложен известным американским электротехником и физиком О. Хевисайдом (1892 г.). Он предложил формальные правила обращения с оператором d, dx и некоторыми функциями от этого оператора, используя которые решил ряд важнейших задач электродинамики. Однако операционное исчисление не получило в трудах О. Хевисайда математического обоснования (его математика возникала в физическом контексте, из которого ее нелегко было выделить, многие его результаты оставались недоказанными. Лишь в 20-е годы XX века метод получил обоснование в работах Бромвича и Карсона. Операционный метод решения дифференциальных уравнений можно сравнить с вычислением различных выражений при помощи логарифмов, когда, например, при умножении вычисления ведутся не над самими числами, а над их логарифмами, что приводит к замене умножения более простой операцией – сложением. Так же как и при логарифмировании, при использовании операционного метода нужны: 1) таблица оригиналов и соответствующих им изображений; 2) знание правил выполнения операций над изображением, соответствующих действиям, производимым над оригиналом. Определение. Функцией- оригиналом - называют функцию f(t) действительного аргумента t, удовлетворяющую условиям: 1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е. f(t) 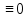 при t<0 при t<02) функция f(t) при t>0 возрастает не быстрее показательной функции, т.е. существуют такие постоянные M>0, S ≥0 , что |f(t)|≤M 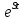 при t>0 при t>03) на любом конечном отрезке положительной полуоси Ot функция f(t)и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода. Простейшей функцией - оригиналом является единичная функция Хевисайда: 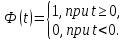 (1) (1)Если функция 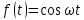 не удовлетворяет условию (1), то произведение не удовлетворяет условию (1), то произведение 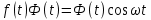 уже ему удовлетворяет, т.е. будет оригиналом. уже ему удовлетворяет, т.е. будет оригиналом.Преобразование Лапласа. Теоремы преобразования Лапласа. Преобразование Лапласа — интегральное преобразование, связывающее функцию F(S) комплексного переменного (изображение) с функцией f(x)  действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Виды преобразований Лапласа: 1. Прямое преобразование Лапласа. Преобразованием Лапласа функции действительной переменной f(t), называется функция F(S) комплексной переменной 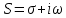 , такая что: , такая что: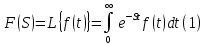 Правая часть этого выражения называется интегралом Лапласа. 2. Обратное преобразование Лапласа. Обратным преобразованием Лапласа функции комплексного переменного 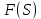 , называется функция , называется функция 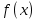 действительного переменного, такая что: действительного переменного, такая что: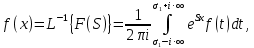 где 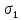 — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича. — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.3. Двустороннее преобразование Лапласа. Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции 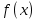 участвуют значения x < 0/ участвуют значения x < 0/Двустороннее преобразование Лапласа определяется следующим образом: 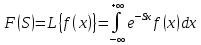 4. Дискретное преобразование Лапласа. Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций. Различают D-преобразование и Z-преобразование. D-преобразование Пусть 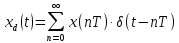 - решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени 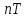 , где n- целое число, а , где n- целое число, а 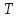 - период дискретизации. Тогда применяя преобразование Лапласа получим: - период дискретизации. Тогда применяя преобразование Лапласа получим: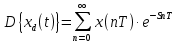 Z-преобразование Если применить следующую замену переменных: 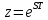 получим Z-преобразование: 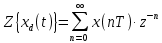 Преобразование Лапласа обладает следующими линейными свойствами: Преобразование суммы функций равно сумме преобразований этих функций: 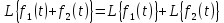 Постоянный множитель можно выносить за знак преобразования: 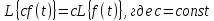 Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований: 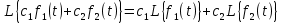 На конкретном примере рассмотрим преобразование Лапласа. Пример. Найти изображение функции 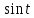 . .Решение: Используем формулу: 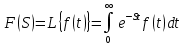 для функции 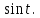 Тогда получим: 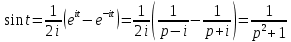 Перейдем к изучению некоторых основных свойств преобразования Лапласа: Теорема подобия. Для любого 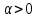 , , 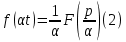 Доказательство: Подстановка 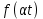 в формулу (1) и замена переменного в формулу (1) и замена переменного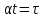 приводит к результату (2): приводит к результату (2):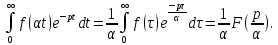 Теорема запаздывания. Для любого 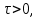 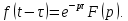 Теорема смещения. Для любого комплексного числа 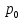 , ,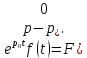 Доказательство свойства (3) элементарно путем подстановки его левой части в интеграл (1). Дифференцирование оригинала. Если функция 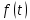 непрерывна при непрерывна при 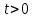 и и 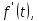 или в более общем случае или в более общем случае 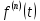 являются оригиналами, то являются оригиналами, то 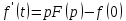 или 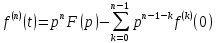 , ,где под 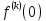 понимается предел справа в точке t=0 понимается предел справа в точке t=0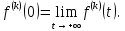 Дифференцирование изображения. Дифференцирование изображения сводится к умножению оригинала на (-t), то есть 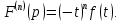 Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на p, то есть: 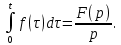 На основе рассмотренных теорем можно составить таблицу преобразования Лапласа. В таблице (рисунок 1) приведены наиболее часто встречающиеся преобразования. Здесь 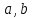 - различные постоянные. - различные постоянные.
Рисунок 1-таблица преобразований Лапласа. 1.3.Решение линейных систем обыкновенных дифференциальных уравнений Дифференциальное уравнение - уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Порядок дифференциального уравнения - наибольший порядок производных, входящих в него. Процесс решения дифференциального уравнения называется интегрированием. Все дифференциальные уравнения можно разделить на линейные и не линейные. Нелинейное дифференциальное уравнение - дифференциальное уравнение (обыкновенное или с частными производными), в которое по крайней мере одна из производных неизвестной функции (включая и производную нулевого порядка - саму неизвестную функцию) входит нелинейно. Иногда под Н.Д.У. понимается наиболее общее уравнение определенного вида. Напр., нелинейнымобыкновенным дифференциальным уравнением 1-го порядка наз. уравнение Н. д. у. с частными производными 1-го порядка для неизвестной функции z от независимых переменных где F- произвольная функция своих аргументов; Решение дифференциальных уравнений - основное приложение операционного метода, основанного на преобразовании Лапласа. Операционный метод включает следующие этапы: преобразование дифференциального уравнения с заданными начальными условиями по Лапласу; при этом образуется комплексное алгебраическое уравнение относительно изображения неизвестной функции; решение комплексного алгебраического уравнения; отыскание оригинала, искомого частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям. Операционный метод решения системы линейных дифференциальных уравнений включает следующие этапы: преобразование системы дифференциальных уравнений по Лапласу; при этом образуется система линейных алгебраических уравнений относительно изображений искомых функций; решение системы алгебраических уравнений, например, методом Крамера; отыскание оригиналов методами обратного преобразования Лапласа. Способ операционного исчисления применим к системе ДУ, когда задание сформулировано следующим образом: Найти частное решение однородной системы дифференциальных уравнений 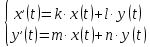 , соответствующее начальным условиям , соответствующее начальным условиям 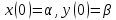 . .Как вариант, система может быть и неоднородной – с «довесками» в виде функций 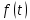 и и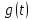 в правых частях: в правых частях: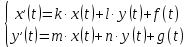 Но, и в том, и в другом случае нужно обратить внимание на два принципиальных момента условия: Речь идёт только о частном решении. В скобочках начальных условий 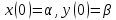 находятся строго нули, и ничто другое. находятся строго нули, и ничто другое.Общий ход и алгоритм будет очень похож на решение дифференциального уравнения операционным методом. Из справочных материалов потребуется в решении линейных систем обыкновенных дифференциальных уравнений таблица преобразований Лапласа. Глава 2. Эмпирические аспекты курсовой работы 2.1. Пример №1 решения линейных систем обыкновенных дифференциальных уравнений С помощью операционного исчисления найти частное решение системы дифференциальных уравнений, соответствующее заданным начальным условиям. 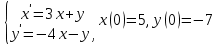 . .Решение: Начало такое: с помощью таблицы преобразования Лапласа перейдем от оригиналов к соответствующим изображениям. В задаче с системами ДУ данный переход обычно прост: Используя табличные формулы, учитывая начальное условие 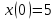 , получаем: , получаем: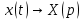 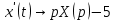 С переменную y проделываем тот же самый путь, меняя в таблице «x» на «y». Используя те же преобразования, учитывая начальное условие 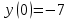 , находим: , находим: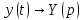 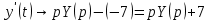 Подставим найденные изображения в исходное уравнение: 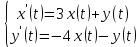 : :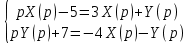 Теперь в левых частях уравнений нужно собрать все слагаемые, в которых присутствует 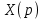 или или 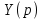 . В правые частиуравнений необходимо перенести все остальные слагаемые: . В правые частиуравнений необходимо перенести все остальные слагаемые: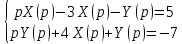 Далее в левой части каждого уравнения проводим вынесение за скобки: 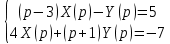 При этом на первых позициях следует разместить При этом на первых позициях следует разместить 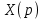 , а на вторых позициях , а на вторых позициях 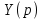 : :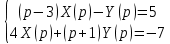 Полученную систему уравнений с двумя неизвестными 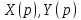 обычно решают по формулам Крамера. Вычислим главный определитель системы: обычно решают по формулам Крамера. Вычислим главный определитель системы: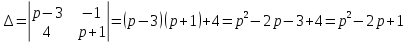 В результате расчёта определителя получен многочлен 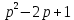 . .Далее идет важный технический прием. Данный многочлен лучше сразу же попытаться разложить на множители. В этих целях следовало бы попробовать решить квадратное уравнение 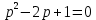 , но сразу можно заметить, что , но сразу можно заметить, что 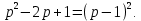 . .Таким образом, наш главный определитель системы: 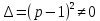 , значит система имеет единственное решение. , значит система имеет единственное решение.Дальнейшее решение проведем по методу Крамера: 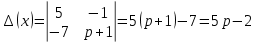 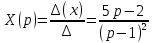 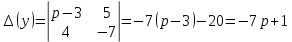 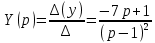 В итоге получаем операторное решение системы: 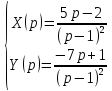 Преимуществом рассматриваемого задания является та особенность, что дроби обычно получаются несложными, и разбираться с ними значительно проще, нежели с дробями в задачах нахождения частного решения ДУ операционным методом. Далее решаем методом неопределенных коэффициентов, с помощью которого раскладываем каждую дробь на элементарные дроби: Разбираемся с первой дробью: 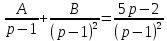 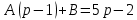 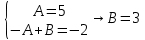 Таким образом: Таким образом: 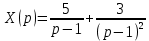 Вторую дробь разваливаем по аналогичной схеме, при этом корректнее использовать другие константы (неопределенные коэффициенты): 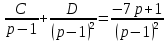 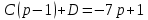 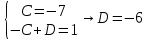 Таким образом: Таким образом: 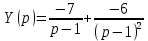 . .В результате операторное решение системы: 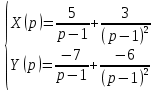 Также операторное решение можно записать в следующем виде: 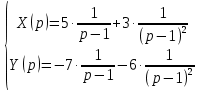 – так будет понятней завершающий этап – обратное преобразование Лапласа. – так будет понятней завершающий этап – обратное преобразование Лапласа.Перейдем от изображений к соответствующим оригиналам: 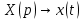 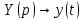 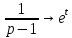 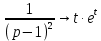 Подставим полученные изображения в операторное решение системы: 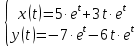 По правилам  можно вынести за скобки, и тогда мы получим правильный ответ. можно вынести за скобки, и тогда мы получим правильный ответ. Ответ: 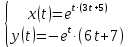 . . Рассмотрим линейное дифференциальное уравнение 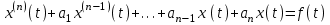 где ak–действительные числа. Требуется найти решение данного дифференциального уравнения, удовлетворяющее начальным условиям x(0)=x0, x`(0)=x`0, …, x(n-1)(0)=x0(n-1) где x0, x`0, …, x0(n-1) – заданные числа. Будем предполагать, что искомая функция x(t), все ее производные, а также функция f (t) являются оригиналами. Пусть 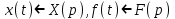 . По формулам дифференцирования оригиналов . По формулам дифференцирования оригиналов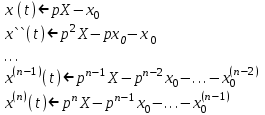 Перейдем от данного дифференциального уравнения к уравнению в изображениях 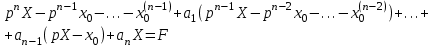 Перепишем его так 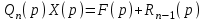 , где , где 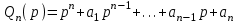 , а , а 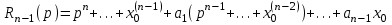 Находим так называемое операторное решение уравнения 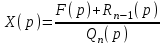 Найдя оригинал x(t) по его изображению X(p) , мы получим тем самым решение задачи Коши для исходного дифференциального уравнения. Пример 1. Найти решение дифференциального уравнения x(t)4x(t)5x(t)0, удовлетворяющее условиям x(0) 0, x(0) 1. Решение. Запишем уравнение в изображениях 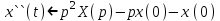 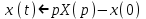 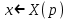 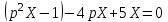 Вынесем Х за скобки 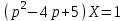 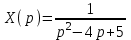 Найдем оригинал используя выведенные ранее значения в таблице приложения: 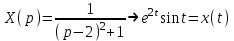 искомое решение - 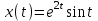 Пример 2. Решить дифференциальное уравнение y`-2y=0, y(0)=1. Решение 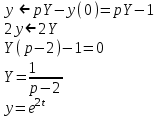 Пример 3. Решить дифференциальное уравнение y`+y=et, y(0)=0. Решение 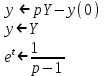 Перейдем к уравнению 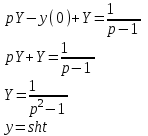 Пример 4. Найти решение уравнения 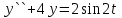 при начальных условиях y(0)=-1, y`(0)=0. при начальных условиях y(0)=-1, y`(0)=0.Решение Пусть 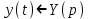 , тогда , тогда 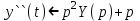 , , 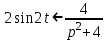 . .Тогда 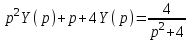 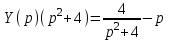 - изображающее уравнение. Отсюда - изображающее уравнение. Отсюда 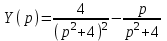 Оригинал для правого слагаемого известен 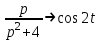 , а оригинал для , а оригинал для 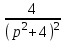 удобнее найти по теореме свертывания. удобнее найти по теореме свертывания.Известно, что 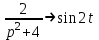 , поэтому , поэтому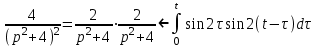 Так как 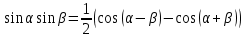 , то , то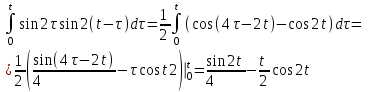 Таким образом, 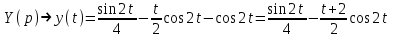 2.2. Пример №2 решения линейных систем обыкновенных дифференциальных уравнений Методом операционного исчисления найти частное решение системы дифференциальных уравнений 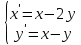 с заданными начальными условиями с заданными начальными условиями 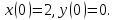 Решение: Перейдем от оригиналов к соответствующим изображениям: 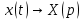 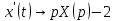 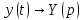 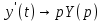 Подставим найденные изображения в исходную систему ДУ: 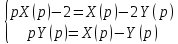 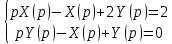 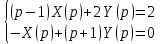 Систему решим по формулам Крамера: 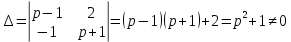 , значит, система имеет единственное решение. , значит, система имеет единственное решение.Полученный многочлен 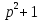 не раскладывается на множители. В этом случае многочлен можно оставить и в таком виде. не раскладывается на множители. В этом случае многочлен можно оставить и в таком виде. 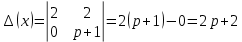 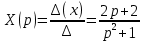 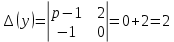 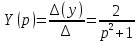 В результате операторное решение системы: 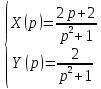 В данном случае метод неопределённых коэффициентов использовать не нужно. В целях применения табличных преобразований перепишем решение в следующем виде: 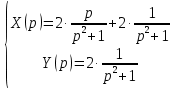 Перейдем от изображений к соответствующим оригиналам: 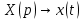 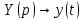 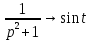 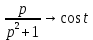 Подставим полученные изображения в операторное решение системы:  Ответ: частное решение:  . . Здесь метод операционного исчисления действительно проще, чем «обычный» способ решения. Заключение Итак, как мы видим, при решении линейных систем обыкновенных дифференциальных уравнений необходимо от дифференциальных уравнений относительно искомой функции-оригинала 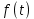 перейти к уравнению относительно другой функции перейти к уравнению относительно другой функции 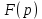 , называемой изображением , называемой изображением 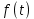 . Полученные (операционные) уравнения обычно уже алгебраические (значит более простое по сравнению с исходным). Решая их относительно изображения . Полученные (операционные) уравнения обычно уже алгебраические (значит более простое по сравнению с исходным). Решая их относительно изображения 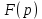 и переходя затем к соответствующему оригиналу, находят искомые решения данной системы дифференциальных уравнений. и переходя затем к соответствующему оригиналу, находят искомые решения данной системы дифференциальных уравнений.Можно сделать вывод, что операционный метод решения систем дифференциальных уравнений можно сравнить с вычислением различных выражений при помощи логарифмов, когда, например, при умножении вычисления ведутся не над самими числами, а над их логарифмами, что приводит к замене умножения более простой операцией – сложением. Так же как и при логарифмировании, при использовании операционного метода нужны: 1) таблица оригиналов и соответствующих им изображений; 2) знание правил выполнения операций над изображением, соответствующих действиям, производимым над оригиналом. В ходе нашей работы цель, поставленная нами, была достигнута, то есть мы изучили особенности операционного метода и преобразований Лапласа при решении линейных систем обыкновенных дифференциальных уравнений. Таким образом, задачи были решены, а именно мы: 1. Изучили состояние операционных исчислений. 2. Выявили основные преобразования Лапласа. 3. Определили теоретические основы операционных исчислений, преобразований Лапласа. 4. Привели примеры решений линейных систем обыкновенных дифференциальных уравнений. Список использованных источников Старков, В.Н. Операционное исчисление и его применения. /В.Н. Старков// Учебн. пособ.; -СПб, 2010. Белослюдова, В.В. Специальные разделы математики. Часть 1. Элементы теории функций комплексной переменной. Операционное исчисление: курс лекций для студентов второго курса специальностей 050702, 050716; /В.В. Белослюдова, И.П. Дронсейка// ВКГТУ. – Усть – Каменогорск, 2006. Данко, П.Е. Высшая математика в упражнениях и задачах. Часть 2./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова// Москва, 2005. Ершова, В.В. Импульсные функции. Функции комплексной переменной. Операционное исчисление./В.В. Ершова// Под ред. В.И. Азаматовой. Минск, 1976. Смышляева, Л.Г. Преобразования Лапласа функций многих переменных. / Л.Г. Смышляева// Изд-во ЛГУ, 1981 Рудаков, А.В. Операционные системы и среды: Учебник / А.В. Рудаков.// - М.: Инфра-М, 2016. - 480 c. Спиридонов, Э.С. Операционные системы / Э.С. Спиридонов, М.С. Клыков, М.Д. Рукин.// - М.: КД Либроком, 2015. - 350 c. Батаев, А.В. Операционные системы и среды: Учебник / А.В. Батаев, Н.Ю. Налютин, С.В. Синицын и др.// - М.: Academia, 2018. - 271 c. Агафонов, С., А. Обыкновенные дифференциальные уравнения / С. А. Агафонов, Т.В. Муратова. - М.: Academia, 2018. - 352 c. Амелькин, В.В. Дифференциальные уравнения в приложениях / В.В. Амелькин. - М.: КД Либроком, 2012. - 208 c. Босс, В. Лекции по математике: Дифференциальные уравнения / В. Босс. - М.: Ленанд, 2019. - 208 c Васильева, А.Б. Дифференциальные и интегральные уравнения. Вариационное исчисление в примерах и задачах / А.Б. Васильева и др. - М.: Физматлит, 2005. - 432 c. Муратова, Т.В. Дифференциальные уравнения: Учебник и практикум для академического бакалавриата / Т.В. Муратова. - Люберцы: Юрайт, 2016. - 435 c. Шалдырван, В.А. Руководство по решению обыкновенных дифференциальных уравнений: Линейные дифференциальные уравнения высших порядков. Граничные задачи для ОДУ. Понятие / В.А. Шалдырван, К.В. Медведев. - М.: КД Либроком, 2012. - 248 c Эльсгольц, Л.Э. Дифференциальные уравнения / Л.Э. Эльсгольц. - М.: Издательство ЛКИ, 2019. - 312 c. |

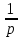
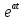
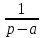
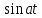
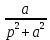
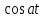
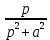
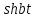
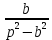
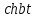
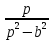
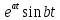
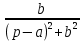
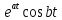
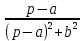
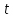
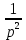
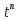
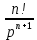
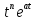
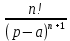
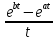
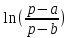
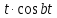
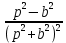
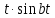
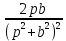
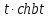
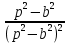
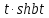
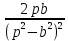
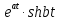
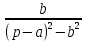
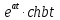
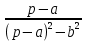
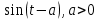
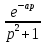
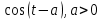
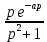
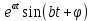
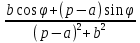
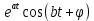
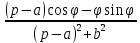
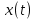
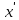 (t)
(t)