Расчетно-графическая работа по высшей математике. РГР2 Вариант№13. Операторы дифференцирования и интегрирования
 Скачать 174.32 Kb. Скачать 174.32 Kb.
|
|
Санкт-Петербургский университет Государственной противопожарной службы МЧС России Кафедра высшей математики и системного моделирования сложных процессов Расчетно-графическая работа по дисциплине: «Высшая математика» тема: «Операторы дифференцирования и интегрирования» Вариант №13 Выполнил студент гр. №60.121.3 ПБ ИБЖ1158 Чернышов Артём Александрович «28» мая 2022г. Санкт-Петербург 2022 1. Исследовать данные функции методами дифференциального исчисления и построить их графики. 13. 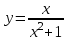 1) 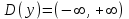 2) 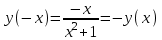 нечетная функция 3) Наклонные асимптоты: 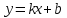 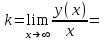 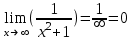 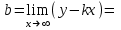 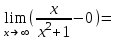 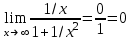 y=0 асимптота 4) Точки экстремума: 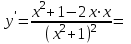 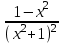 Приравняем производную к нулю 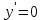 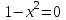 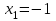 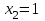  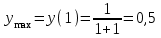 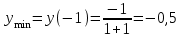 функция возрастает на 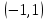 функция убывает на 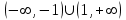 5) Точки перегиба: 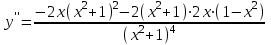 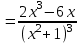 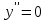 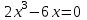 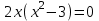  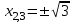 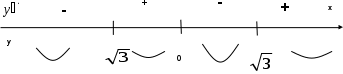 функция выпукла вверх на 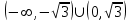 функция вогнута вниз на 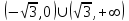 6) Точки пересечения с осями: Ох: у=0 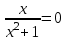 х=0 (0,0) Оу: х=0 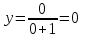 (0, 0) 7) График функции: 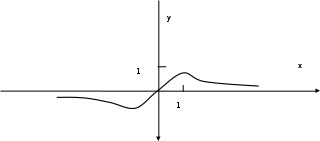 2. Найти производные заданных функций 13. а) 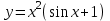 б) б) 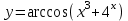 в) в) 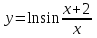 Решение: а) 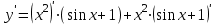 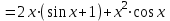 б) 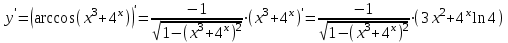 в) 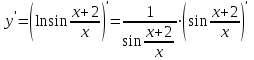 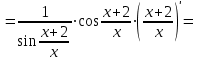 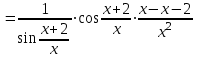 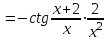 3. найти дифференциалы второго порядка. 13. 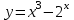 Решение: 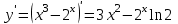 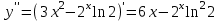 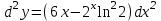 4. Найти площади фигур, ограниченных линиями. Сделать чертеж. 13. 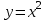 y=9 y=9 Решение: найдем абсциссы точек пересечения: 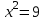 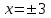 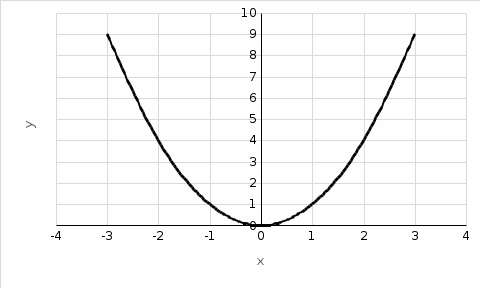 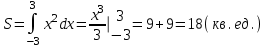 5. Найти неопределенные интегралы. 13. а) 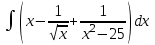 б) б) 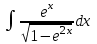 в) в) 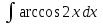 решение: а) 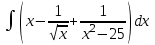 = =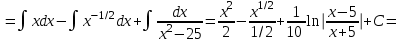 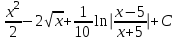 б) 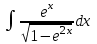 Замена: 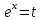 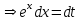 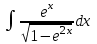 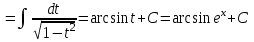 в) 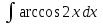 Интегрирование по частям: 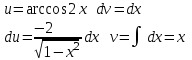 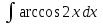 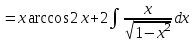 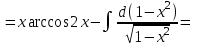 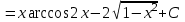 6. Вычислить определенные интегралы. 13. а) 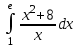 б) б) 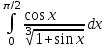 Решение: а) 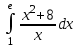 = =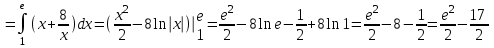 б) 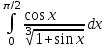 = =Замена: 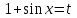 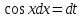 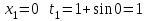 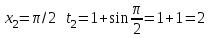 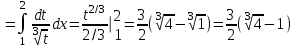 7. Вычислить несобственные интегралы. 13. 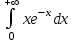 Интегрирование по частям: 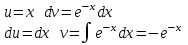 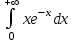 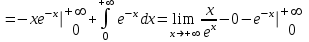 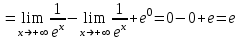 8. Найти объем тела, с помощью определенного интеграла. 7. найти объем тела образованного вращением вокруг оси Оу ограниченной параболой: 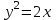 и прямой у=0 2х+2у-3=0 и прямой у=0 2х+2у-3=0Решение:  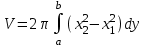 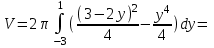 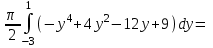 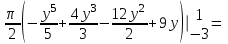 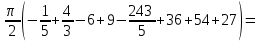 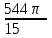 |
