Описание и анализ данных
 Скачать 46.15 Kb. Скачать 46.15 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) КАФЕДРА ИС Практическая работа №2 По дисциплине «Статистический анализ» Тема: «Описание и анализ данных» Вариант: город Сеул
Оформление отчёта: Поспелова Е.И. Дата сдачи: 20.04.2002 Преподаватель: к.т.н., доцент Бурков Е.А. Санкт-Петербург 2022 Цель работы. Анализ предложенного набора данных с помощью базовых статистических характеристик и доверительных интервалов. Постановка задачи. Построить доверительный интервал уровня 1–α для среднегодовой температуры в выбранном для анализа городе, принимая здесь и далее значение α равным числу своего рождения, деленному на 200. Например, если дата рождения 18 марта, то α = 0.09. С помощью построенного доверительного интервала оценить достоверность гипотезы о равенстве среднегодовой температуры 10 градусам по Цельсию. С помощью критерия хи-квадрат проверить гипотезу о том, что стандартное отклонение среднегодовой температуры не превышает значения стандартного отклонения этой величины, найденного в 1-й практической работе. На основании результатов 1-й практической работы выбрать для анализа один из четырех сезонов, среднемесячная температура в месяцах которого распределена достаточно близко к нормальному закону (обосновать выбор, приведя часть результатов предыдущей работы), и рассчитать средневзвешенную температуру выбранного сезона, получив значение средне сезонной температуры (ast). С помощью критерия Стьюдента проверить следующие статистические гипотезы: 1) Средняя температура первого месяца сезона больше ast. 2) Средняя температура второго месяца сезона равна ast. 3) Средняя температура третьего месяца сезона меньше ast. 6. Используя критерий Стьюдента и поправку Бонферрони проверить для выбранного сезона гипотезу о том, что все три выборки значений среднемесячной температуры извлечены из одной генеральной совокупности. Выполнение работы Построить доверительный интервал уровня 1–α для среднегодовой температуры в выбранном для анализа городе, принимая здесь и далее значение α равным числу своего рождения, деленному на 200. Например, если дата рождения 18 марта, то α = 0.09. Интервальная оценка, доверительный уровень которой равен 95%, интерпретируется следующим образом: если из генеральной совокупности извлечь все выборки, имеющие объем n, и вычислить их выборочные средние, то 95% доверительных интервалов, построенных на их основе, будут содержать математическое ожидание генеральной совокупности, а 5% — нет. Интервал в интервальной оценке называется доверительным интервалом (confidence interval, CI), а вероятность того, что истинное значение параметра находится в этом интервале, называется доверительной вероятностью (надежностью): 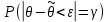 . (1) . (1)Построим доверительный интервал с помощью RStudio. Выборочная оценка стандартной ошибки среднего равно: 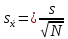 , где s – стандартное отклонение, N – объём выборки. , где s – стандартное отклонение, N – объём выборки. Чтобы построить доверительный интервал, для каждого месяца нужны стандартная ошибка, средние значение выборки, стандартное отклонение и объём выборки. Все эти значения, за исключением стандартной ошибки, были высчитаны в Практической работе №1, поэтому данные будем брать оттуда. Интервал формируется следующей формулой: 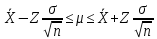 (2) (2)Стандартная ошибка формируется с помощью функции 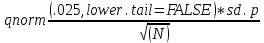 (3) (3)Рассчитаем ошибку за год:
Теперь, когда у нас есть стандартная ошибка, для построения доверительного интервала нужно просчитать нижнюю и верхнюю границу. Границы рассчитываются по формуле: 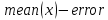 , ,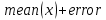 Тогда доверительный интервал для каждого месяца и за год получится:
Теперь просчитаем со значением α = 0.03. (Т.к. берем дату дня рождения 05.09, соответственно 05.09/200 = 0,025 = 0.03) Тогда доверительный интервал при построении в R будет иметь вид: 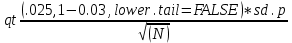 (5) (5)
С помощью построенного доверительного интервала оценить достоверность гипотезы о равенстве среднегодовой температуры 10 градусам по Цельсию. Гипотеза о том, что параметр генеральной совокупности равен ожидаемому, называется нулевой. Тогда, учитывая наши данные, генеральная совокупность есть среднее от выборки погоды за год. Тогда статус-кво нулевой гипотезы будет равен 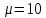 . .Гипотеза, которая считается истинной, есть ложная нулевая гипотеза. Т.е. 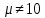 . .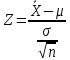 (6) (6)Числитель – отклонение выборочного среднего от математического ожидания генеральной совокупности. Знаменатель – стандартное отклонение, деленное на корень квадратный из объёма выборки. Таким образом, статистика Z выражает разность между выборочным средним и математическим ожиданием, выраженную в единицах стандартного отклонения. Возьмем уровень значимости равным 0.05, тогда размер критической области также будет равен 0.05. Возьмем выборку из 25 случайных значений из всех значений, полученных за год. Допустим, что средняя температура за год, содержащаяся в новой выборке, равна 11.676, а стандартное отклонение равно 0.993. Тогда 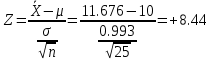 (7) (7)В качестве статистического метода и соответствующую статистику, возьмем z-статистику. Т.к. стандартное отклонение известно заранее. Теперь создадим функцию для использования z-критерия для проверки гипотез о математическом ожидании: z.test = function(x,mu,popvar){ z.score <- round((mean(x)-mu)/(popvar/sqrt(length(x))),3) one.tail.p <- round(pnorm(abs(z.score),lower.tail = FALSE),3) cat(" z = ", z.score, "\n", "one-tailed probability =", one.tail.p, "\n", "two-tailed probability =", 2*one.tail.p) } Данные, которые мы получили в результате выполнения этой функции: z = 0 one-tailed probability = 0.5 two-tailed probability = 1 Так как условие стояло именно о равенстве среднегодовой температуры 10 градусам, то смотрим на двусторонний критерий. Он равен 1, что больше 0.05, соответственно, это говорит о том, что нужно принять нулевую гипотезу. Т.е. что среднегодовая температура НЕ равна 10. С помощью критерия хи-квадрат проверить гипотезу о том, что стандартное отклонение среднегодовой температуры не превышает значения стандартного отклонения этой величины, найденного в 1-й практической работе. Критерий хи-квадрат применяется в случае, если вопрос стоит в виде «Равны ли дисперсия или стандартное отклонение заданной величине?». 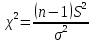 (8) (8)В нашем случае нас интересует, отличается ли стандартное отклонение среднегодовой температуры от стандартного отклонения, что было найдено в 1-й практической работе. В 1-й практической работе стандартное отклонение среднегодовой температуры имеет значение, равное 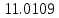 Можно применить двусторонний критерий, а нулевую и альтернативную гипотезу сформулировать следующим образом: 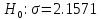 , ,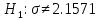 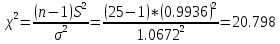 Т.к. 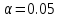 , число степеней свободы = 24. Исходя из этого, можно установить критические значение. Левое – 12.401, правое – 39.364. , число степеней свободы = 24. Исходя из этого, можно установить критические значение. Левое – 12.401, правое – 39.364.Значение критерия хи-квадрата входит в область принятия гипотезы о том, что стандартное отклонение среднегодовой температуры не превышает значения стандартного отклонения этой величины, найденного в 1-й практической работе. На основании результатов 1-й практической работы выбрать для анализа один из четырех сезонов, среднемесячная температура в месяцах которого распределена достаточно близко к нормальному закону (обосновать выбор, приведя часть результатов предыдущей работы), и рассчитать средневзвешенную температуру выбранного сезона, получив значение средне сезонной температуры (ast). По результатам из первой практической работы, лето, зима и весна показывают слабовыраженную асимметрию и большой коэффициент асимметрии, что говорит о том, что данные дальше всего распределены к нормальному закону. 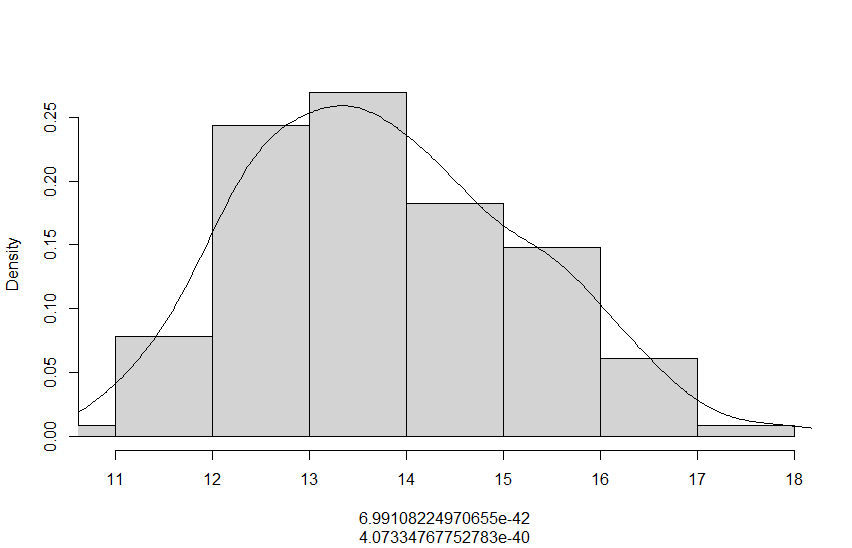 Рисунок 1 – Гистограмма средней температуры в октябре 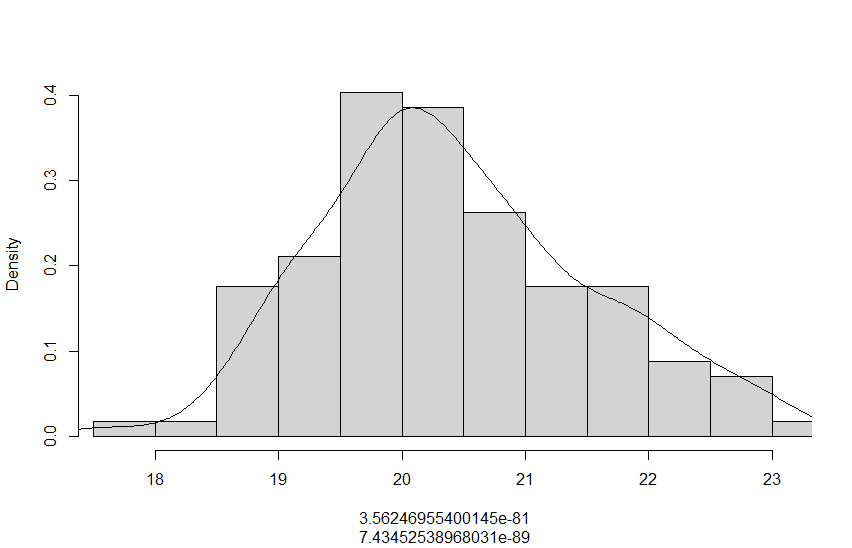 Рисунок 2 – Гистограмма средней температуры в сентябре  Рисунок 3 – Гистограмма средней температуры в сентябре Найдем средне сезонную температура (Осень). 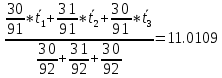 С помощью критерия Стьюдента проверить следующие статистические гипотезы: 1) Средняя температура первого месяца сезона больше ast. 2) Средняя температура второго месяца сезона равна ast. 3) Средняя температура третьего месяца сезона меньше ast. Одно выборочный вариант критерия Стьюдента служит для проверки нулевой гипотезы о равенстве среднего значения генеральной совокупности, из которой была взята выборка, некоторому известному значению (например, H0: μ = 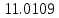 ) и рассчитывается как отношение разницы между выборочным средним и известным значением к стандартной ошибке выборочного среднего: ) и рассчитывается как отношение разницы между выборочным средним и известным значением к стандартной ошибке выборочного среднего: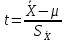 (10) (10)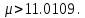 Возьмем уровень значимости Возьмем уровень значимости 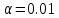 , , 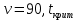 = 2,632 = 2,632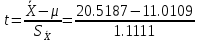 = 8.55 = 8.55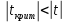 не является правдой. Тем самым, мы не попадаем в зону принятия нулевой гипотезы. А значит, что не принимаем нулевую гипотезу. не является правдой. Тем самым, мы не попадаем в зону принятия нулевой гипотезы. А значит, что не принимаем нулевую гипотезу. 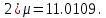 Возьмем уровень значимости Возьмем уровень значимости 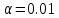 , , 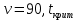 = 2,632 = 2,632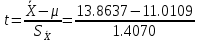 = 2,0275 = 2,0275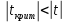 является правдой. Тем самым, мы попадаем в зону принятия нулевой гипотезы. А значит, что принимаем нулевую гипотезу. является правдой. Тем самым, мы попадаем в зону принятия нулевой гипотезы. А значит, что принимаем нулевую гипотезу. 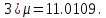 Возьмем уровень значимости Возьмем уровень значимости 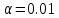 , , 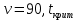 = 2,632 = 2,632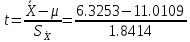 = -2,544 = -2,544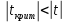 является правдой. Тем самым, наше значение находится правее от критического, значит находится в зоне принятия гипотезы. Соответственно, принимаем нулевую гипотезу. является правдой. Тем самым, наше значение находится правее от критического, значит находится в зоне принятия гипотезы. Соответственно, принимаем нулевую гипотезу. |
